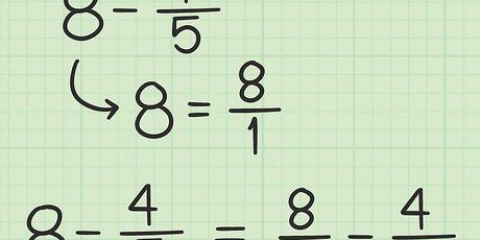tu dovrai "prestare" dei 3 pollici "32" per fare il 2 un 12. Attraversa il 3 di "32" e rendilo un 2, quindi rendi l`unità 2 un 12. Ora hai 12 – 7 = 5. Scrivi un 5 sotto la colonna delle unità. 



Quindi nella prima somma, 15 - 9, la risposta diventa positiva, perché 15 è maggiore di 9. Quindi nella seconda somma, 2 - 30, la risposta diventa negativa, perché 2 è inferiore a 30. 
Per il problema 15 - 9, prendi 15 monete. Rimuovi 9 e conta quanti ne sono rimasti (6). Quindi, 15 - 9 = 6. Oppure usa una linea numerica e disegna i numeri da 1 a 15 lungo la linea, quindi cancella 9 da 15 in giù per arrivare a 6. Con la somma 2 – 30 è più facile invertire i numeri e rendere la risposta negativa. Quindi, 30 - 2 = 28, e con questo 2 – 30 è -28. 

Non dimenticare di includere il punto decimale (la virgola) nella risposta. Ora si presenta così: ,2. 




Si noti che lcm di due numeri non è sempre uno dei due numeri. Ad esempio, a 3 e 2, l`LCF è 6, perché non esiste un numero inferiore a 6 che è un multiplo di ciascuno dei numeri. 
Quindi il nuovo compito sarà: 13/10 - 6/10. 









3x - 2x = x -5x - 2x = -7x 2y - y = y -z - 0 = -z 
3x - 5x + 2y - z - (2x + 2x + y) = x - 7x + y - z
Sottrai numeri
Contenuto
Le sottrazioni sono quelle somme in cui si sottraggono due numeri l`uno dall`altro. È abbastanza semplice se vuoi sottrarre numeri interi l`uno dall`altro, ma diventa un po` più complicato quando lavori con frazioni o decimali. Una volta che hai imparato la sottrazione, puoi passare ai concetti matematici più complicati e aggiungere, moltiplicare e dividere numeri sarà molto più semplice.
Passi
Metodo 1 di 6: sottrai numeri interi grandi prendendo in prestito

1. Annota il numero più grande. Supponiamo di lavorare con la somma 32 - 17. Scrivi prima 32.

2. Scrivi il numero più piccolo direttamente sotto di esso. Assicurati che le decine e le unità siano ben allineate in modo che i 3 pollici "32" direttamente sopra 1 pollice "17" stato e il 2 in "32" direttamente sopra il "7" alle 17.

3. Sottrai il numero in basso dall`alto. Questo può diventare un po` complicato se il numero in basso è maggiore di quello in alto. In questo caso 7 è maggiore di 2. Ecco cosa fare:

4. Sottrarre il dieci nel numero in basso dai dieci nel numero in alto. Non dimenticare che il 3 di 32 è diventato un 2. Ora sottrai 1 su 17 dal 2 sopra, quindi 2-1= 1. Scrivi 1 sotto la colonna delle decine. Se tutto va bene, ora hai 15 come risposta, quindi 32 - 17 = 15.

5. Controlla il tuo lavoro. Se vuoi essere sicuro di aver eseguito correttamente il calcolo, tutto ciò che devi fare è aggiungere la risposta al numero più piccolo per ottenere il numero più grande indietro. Quindi per controllare: 15 + 17 = 32, quindi hai fatto bene. Eccellente!
Metodo 2 di 6: sottrarre numeri interi piccoli

1. Determina quale numero è maggiore. Un esercizio come 15 - 9 richiede un approccio diverso da 2 - 30.
- Nella somma 15 - 9, il primo numero, 15, è il più grande.
- Nella somma 2 - 30, il secondo numero, 30 è il più grande.

2. Decidi se la tua risposta deve essere positiva o negativa. Se il primo numero è il più grande, la risposta è positiva. Se il secondo numero è il più grande, la risposta è negativa.

3. Trova la differenza tra i due numeri. Per sottrarre due numeri, calcola la differenza tra loro.
Metodo 3 di 6: sottrazione dei decimali

1. Scrivi il numero più grande sopra il numero più piccolo in modo che i decimali siano allineati. Supponiamo di avere il seguente problema: 10.5 - 8.3. Scrivi il 10.5 sopra 8.3 in modo tale che le virgole siano una sopra l`altra.
- Se hai un problema in cui un numero ha più cifre decimali dell`altro, riempi lo spazio vuoto con zeri. Ad esempio, se hai il problema 5.32 - 4.2, puoi riscriverlo come 5.32 = 4.20. Questo non cambia il valore di un numero, ma ti assicuri che entrambi i numeri possano essere sottratti più facilmente l`uno dall`altro.

2. Sottrarre i decimi l`uno dall`altro. La sottrazione da questi numeri è la stessa degli interi, tranne per il fatto che devi prestare attenzione al punto decimale, allineato e incluso nella risposta. In questo caso devi sottrarre 3 da 5. 5 - 3 = 2, quindi scrivi un 2 sotto il 3 in 8.3.

3. Ora sottrai le unità l`una dall`altra. Ora sottrai 8 da 0. Prendi in prestito una dozzina dell`1 (accanto allo 0) per fare 10, ora sottrai 8 da 10. Puoi anche calcolare immediatamente la somma 10 – 8 = 2, senza il passaggio intermedio del prestito, perché il numero in basso non ha un dieci. Scrivi la risposta sotto 8.

4. Quindi la risposta finale sarà 2.2.

5. Controlla il tuo lavoro. Se vuoi essere sicuro di aver eseguito correttamente il calcolo, tutto ciò che devi fare è aggiungere la risposta al numero più piccolo per ottenere il numero più grande indietro. 2.2 + 8.3 = 10.5 quindi sei a posto.
Metodo 4 di 6: Sottrarre frazioni

1. Metti insieme numeratori e denominatori. Supponiamo che tu stia lavorando con il problema 13/10 - 3/5. Scrivi questo problema in modo che entrambi i numeratori, 13 e 3, ed entrambi i denominatori, 10 e 5, siano uno accanto all`altro, separati da un segno meno. Ciò offre una migliore panoramica del problema e semplifica la ricerca di una soluzione.

2. Trova il minimo comune multiplo. Questo è il più piccolo multiplo di due numeri. L`LCF di 10 e 5 in questo esempio è 10.

3. Riscrivi le frazioni con gli stessi denominatori. La frazione 13/10 può rimanere invariata perché il denominatore non è cambiato, ma la frazione 3/5 diventa uguale a 6/10 perché il denominatore va due volte nel multiplo comune di 10. Ora hai equalizzato entrambe le frazioni. 3/5 è uguale a 6/10, ma con la differenza che ora non è più un problema sottrarre entrambe le frazioni l`una dall`altra.

4. Sottrarre entrambi i numeratori l`uno dall`altro. Quindi 13 - 6 = 7. Non sottrarre i denominatori.

5. Posiziona il nuovo numeratore sopra il nuovo denominatore (l`LCF calcolato in precedenza) per la risposta finale. Il nuovo numeratore è 7 e il denominatore di entrambe le frazioni è 10. Quindi la risposta finale è 7/10.

6. Controlla il tuo lavoro. Se vuoi essere sicuro di aver eseguito correttamente il calcolo, tutto ciò che devi fare è aggiungere la risposta al numero più piccolo per ottenere il numero più grande indietro. Quindi per controllare: 7/10 + 6/10 = 13/10. Ora sei tutto pronto.
Metodo 5 di 6: sottrai una frazione da un numero intero

1. Scrivi il compito. Supponiamo di avere il seguente problema: 5 - 3/4. Nota questo.

2. Converti il numero intero in una frazione con lo stesso denominatore della frazione data. Fai una frazione di 5 con denominatore 4. Consideriamo innanzitutto che 5 è uguale alla frazione 5/1. Quindi moltiplichi sia il numeratore che il denominatore della nuova frazione per 4 per ottenere due frazioni con lo stesso denominatore. Ciò mantiene il valore della frazione lo stesso, ma con numeri diversi. Quindi, 5/1 x 4/4 = 20/4.

3. Riscrivi il compito. Ora può essere scritto come: 20/4 - 3/4.

4. Sottrarre i numeratori delle frazioni e mantenere uguali le frazioni. Quindi, 20 - 3 = 17. Quindi il numeratore finale diventa 17 e il denominatore è 4.

5. Quindi la risposta al problema è 17/4. Per convertire questa frazione impropria in una frazione composta, dividi 17 per 4 per ottenere il numero 4 con resto di 1. La risposta quindi appare così: 4 1/4.
Metodo 6 di 6: Sottrarre variabili

1. Scrivi il compito. Supponiamo di lavorare sul seguente problema: 3x - 5x + 2y - z - (2x + 2x + y). Scrivi la prima equazione sopra la seconda.

2. Sottrai tutti i termini simili l`uno dall`altro. Quando si lavora con le variabili, è possibile sottrarre solo termini con la stessa variabile e con la stessa potenza. Ciò significa che puoi fare 4x -7x, ma non 4x -7x. Quindi puoi dividere questo compito in questo modo:

3. Dai la tua risposta finale. Ora che hai sottratto tutti i termini uguali, puoi dare immediatamente la tua risposta finale. Ecco la risposta:
Consigli
- Rompi i numeri più grandi in pezzi più piccoli. Prendi: 63 - 25.Nessuno sta dicendo che devi sottrarre tutti e 25 in una volta. Puoi prima sottrarre 3 per ottenere 60; quindi sottrai 20 per ottenere 40 e poi gli ultimi 2. Risultato: 38. E ora non devi prendere in prestito.
Avvertenze
- Se hai una combinazione di numeri positivi e negativi, le cose diventano molto più complicate.Continua a cercare articoli che possano aiutarti in questo.
Articoli sull'argomento "Sottrai numeri"
Condividi sui social network:
Popolare