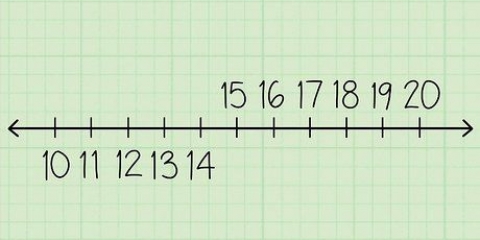1 - 0 = 1 11 - 10 = 1 1011 - 10 = 1001 
110 - 101 = ? 
Per prima cosa cancella 1 e sostituiscilo con uno 0 e ottieni: 110 - 101 = ? Hai sottratto 10 dal primo numero, quindi puoi aggiungere questo numero "preso in prestito" al numero nelle unità: 110 - 101 = ? 
110 - 101 = ? La colonna all`estrema destra è ora:- 1 = 1. Se non sai come arrivare a questa risposta, prova il problema calcola come decimali: 102 = (1 x 2) + (0 x 1) = 210. (Il sub i numeri indicano in quale base è scritto il numero.) 12 = (1x1) = 110. Quindi in forma decimale questa affermazione appare così: 2 - 1 = ?, quindi la risposta è 1. 
110 - 101 = __1 = _01 = 001 = 1. 
11000 - 111 = 1110000 - 111 = (ricorda, 10 - 1 = 1) 111001000 - 111 = Eccolo un po` più breve: 10110 - 111 = Risolvi per colonna: _ _ _ _ 1 = _ _ _ 0 1 = _ _ 0 0 1 = _ 0 0 0 1 = 1 0 0 0 1 
Somma i numeri binari insieme per controllare il tuo lavoro. Aggiungi la risposta alla risposta più piccola e di conseguenza dovresti ottenere il numero più grande. Utilizzando il nostro esempio precedente (11000 - 111 = 10001), otteniamo 10001 + 111 = 11000, che è il numero più grande con cui abbiamo iniziato. Un`altra opzione è convertire qualsiasi numero da binario a decimale per vedere se è giusto. Utilizzando lo stesso esempio (11000 - 111 = 10001), possiamo convertire qualsiasi numero in un decimale, quindi otteniamo 24 - 7 = 17 come risposta. Questo è corretto, quindi la nostra soluzione è corretta. 

101 - 011 = ? 
Fondamentalmente quello che stiamo facendo qui è "prendere il complemento di uno" o sottrarre ogni cifra nel termine da uno. Questo è valido per i numeri binari, poiché ci sono solo due possibili risultati quando si scambia il termine: 1 - 0 = 1 e 1 - 1 = 0. 

101 + 101 = 1010 Se questo non ti è chiaro, leggi di più su addizione di numeri binari. 
1010 = 10Così: 101 - 011 = 10 Se non una cifra in più, hai provato a sottrarre un numero più grande da uno più piccolo. Consulta la sezione Suggerimenti per la risoluzione di tali problemi e ricomincia da capo. 
56 - 17 Poiché utilizziamo i decimali, prendiamo il `complemento di nove` del secondo termine (17) sottraendo ogni cifra da nove. 99 - 17 = 82. Fai una somma di questo: 56+82. Se lo confronti con il problema originale (56-17), vedrai che abbiamo aggiunto 99. 56 + 82 = 138. Ma poiché le nostre modifiche hanno aggiunto 99 al problema originale, dobbiamo sottrarre 99 dalla risposta. Ancora una volta, useremo un modo più veloce, proprio come con il metodo binario sopra: aggiungi 1 al numero totale, quindi rimuovi la cifra a sinistra (che rappresenta 100): 138 + 1 = 139 → 139 → 39 Questa è in definitiva la soluzione al nostro problema originale, 56-17.
Sottrazione di numeri binari
Contenuto
La sottrazione di numeri binari è leggermente diversa con i numeri decimali, ma seguendo i passaggi seguenti è altrettanto facile, se non più facile.
Passi
Metodo 1 di 2: utilizzare il prestito

1. Metti i numeri binari uno sotto l`altro, proprio come con una normale somma meno. Scrivi il numero più grande sopra il numero più piccolo. Se il numero più piccolo ha meno cifre, allinea entrambi i numeri a destra, come faresti con un decimale (base dieci).

2. Prova alcuni semplici esercizi. Per alcuni numeri binari, la sottrazione non è diversa da quella per i numeri decimali. Metti i numeri uno sotto l`altro, inizia da destra e determina il risultato per ogni numero. Ecco alcuni semplici esempi:

3. Ora fai un problema più complicato. Hai solo bisogno di conoscere una "regola" speciale per essere in grado di fare qualsiasi somma negativa con numeri binari. Questa regola ti dice come `prendere in prestito` dal numero a sinistra, per risolvere una colonna `0 - 1`. Per il resto di questa parte, prendiamo alcuni esempi di problemi e risolviamoli usando il prestito. Ecco il primo:

4. `Prestito` dalla seconda cifra. Dalla colonna di destra (le unità), dobbiamo risolvere il problema `0 - 1`. Per fare questo abbiamo bisogno di `prendere in prestito` dalla cifra alla sua sinistra (le coppie). Questo avviene in due fasi:

5. Risolvi per la colonna all`estrema destra. Ora ogni colonna può essere risolta come al solito. Puoi risolvere la colonna all`estrema destra (quella delle unità) di questo problema nel modo seguente:

6. Completa il compito. Il resto del problema ora può essere risolto facilmente. Risolvilo colonna per colonna, da destra a sinistra:

7. Prova un compito più difficile. Il prestito è comune in binario e talvolta devi prendere in prestito più volte per colonna. Ad esempio, risolviamo quanto segue: 11000 -111. Non possiamo "prendere in prestito" da uno 0, quindi continuiamo a prendere in prestito dalla cifra a sinistra finché non diventa qualcosa da cui possiamo prendere in prestito:

8. Controlla la tua risposta. Ci sono sempre tre modi per controllare la tua risposta. Un modo rapido è inserire il problema in a calcolatrice binaria in linea. Gli altri due metodi sono comunque utili, in quanto potrebbero richiedere di controllare manualmente la risposta durante un test e semplificare la gestione dei numeri binari:
Metodo 2 di 2: Utilizzo del metodo del complemento

1. Allinea i due numeri come nella sottrazione decimale. Questo metodo viene utilizzato dai computer per sottrarre numeri binari perché utilizza un programma più efficiente. Per qualcuno che è abituato a sottrarre numeri decimali comuni, questo è probabilmente un metodo più difficile da usare, ma può essere utile per un programmatore capire.
- Usiamo il seguente esempio: 101 - 11 = ?

2. Metti degli zeri davanti ad esso, se necessario, in modo che entrambi i numeri abbiano lo stesso numero di cifre. Ad esempio, converti 101-11 in 101-011 in modo che entrambi i numeri abbiano tre cifre.

3. Scambia i numeri nel secondo termine. Trasforma tutti gli zeri in uno e tutti gli uno in zeri nel secondo termine. Nel nostro esempio, il secondo termine diventa: 011 → 100.

4.Aggiungine uno al nuovo secondo termine. Una volta che hai il termine "inverso", aggiungine uno al risultato. Nel nostro esempio otteniamo 100 + 1 = 101.

5.Risolvi il nuovo problema come addizione binaria. Usa le tecniche di addizione binaria per aggiungere il nuovo termine al termine originale invece di sottrarlo:

6. Ignora la prima cifra. Con questo metodo si finisce sempre con una risposta che è una cifra di troppo. Ad esempio, abbiamo iniziato con numeri di tre cifre ciascuno (101 + 101) ma abbiamo terminato con una risposta a quattro cifre (1010). Cancella la prima cifra e otterrai la risposta all`originale meno somma:

7. Prova questo metodo con i decimali. Questo metodo è chiamato il "complemento a 2"-metodo, perché i passaggi con `invertire i numeri` danno come risultato il `complemento a 1`, dopo il quale viene aggiunto 1. Per capire meglio perché questo metodo funziona, provalo nel sistema dei numeri decimali (base 10):
Consigli
- Per sottrarre un numero più grande da un numero più piccolo, invertire l`ordine dei numeri, calcolare la somma meno e aggiungere un segno meno alla risposta. Ad esempio, per risolvere la somma binaria 11-100, dobbiamo prima calcolare 100-11 e quindi aggiungere un segno meno alla risposta (e questa regola si applica alla sottrazione in qualsiasi base, non solo nei numeri binari).
- Matematicamente, il metodo del complemento usa l`identità a - b = a + (2 - b) - 2 Quando n è il numero di cifre in b, allora 2 - b è uno in più rispetto al risultato della barratura.
Articoli sull'argomento "Sottrazione di numeri binari"
Condividi sui social network:
Popolare