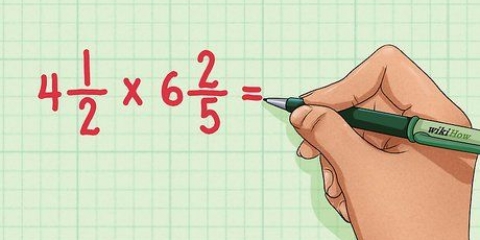11 > 1, quindi 11 "non va bene" 1. Scrivi uno 0 come prima cifra del quoziente (sopra la prima cifra del dividendo). 
Abbassa la cifra successiva del dividendo. 11 > 10. Scrivi uno 0 nel quoziente. Abbassa il numero successivo. 11 < 101. Scrivi un 1 nel quoziente. 
Scrivi il divisore sotto il dividendo. Qui lo scriviamo come 11 sotto le prime tre cifre (101) del dividendo. Calcola 101 - 11 per il resto, 10. Rivedi come sottrarre numeri binari se non ricordi. 
Scrivi 11 sotto 100 e sottrai questi numeri per ottenere 1. Abbassa l`ultima cifra del dividendo e otterrai 11 come risposta. 11 = 11, quindi scrivi 1 come ultima cifra del quoziente (la risposta). Non c`è resto, quindi l`attività è completata. La risposta è 00111, o più semplice, 111. 
La divisione di numeri binari spesso comporta la ripetizione di numeri dopo il punto decimale, più spesso di quelli che si verificano con la notazione decimale. Questo è indicato con il termine più generale "punto radix" che incontri in qualsiasi sistema numerico, perché hai il "punto decimale" incontrati solo all`interno del sistema decimale. 

Trova il complemento di quelli del secondo termine sottraendo ogni cifra da 1. Puoi farlo facilmente con i numeri binari impostando ogni 1 su 0 e ogni 0 su 1. Nel nostro esempio, 011 è uguale a 100. Aggiungi 1 al risultato: 100 + 1 = 101. Questo è chiamato complemento di 2. Consideriamo ora una somma negativa come somma di addizione. L`essenza è che consideriamo il problema come se stessimo aggiungendo un numero negativo invece di sottrarre un numero positivo, dopo aver completato la procedura. Aggiungi il risultato al primo termine. Risolvi la somma: 111 + 101 = 1100. Ometti la prima cifra (porta cifra). Rimuovi la prima cifra dalla tua risposta per ottenere il risultato finale. 1100 → 100. 

complemento a 2 di 000101 = 111010 + 1 = 111011 100011 + 111011 = 1011110 Ometti la prima cifra (il riporto) → 011110 

011110 + 111011 = 1011001 → 011001 (quoziente 1+1=10) 011001 + 111011 = 1010100 → 010100 (quoziente 10+1=11) 010100 + 111011 = 1001111 → 001111 (11+1=100) 001111 + 111011 = 1001010 → 001010 (100+1=101) 001010 + 111011 = 10000101 → 0000101 (101+1=110) 0000101 + 111011 = 1000000 → 000000 (110+1=111) 0 è inferiore a 101, quindi possiamo fermarci ora. Il quoziente 111 è la risposta al sottoproblema. Il resto è il risultato finale del nostro minimo, in questo caso 0 (nessuna pausa).
Divisione di numeri binari
Contenuto
La divisione dei numeri binari può essere risolta usando la divisione lunga, un metodo conveniente per insegnare a te stesso la procedura o scrivere un semplice programma per computer. In alternativa, il metodo del complemento della sottrazione ripetuta offre un approccio con cui potresti non avere familiarità, sebbene non sia molto utilizzato nella programmazione. I linguaggi macchina di solito utilizzano un algoritmo di stima per una maggiore efficienza, ma questi non sono descritti qui.
Passi
Metodo 1 di 2: Usare la divisione lunga

1. Vai di nuovo sulla divisione lunga decimale. Se è passato un po` di tempo dall`ultima volta che hai eseguito la divisione lunga con numeri decimali regolari (base 10), rivedi la sua base per il problema 172 ÷ 4. Altrimenti, salta questo passaggio e vai al passaggio successivo per apprendere questa procedura per i numeri binari.
- Esso dividendo è diviso per il divisore, e la risposta è questa quoziente.
- Confronta il divisore con la prima cifra del dividendo. Se il divisore è il numero più grande, continua ad aggiungere cifre al dividendo finché il divisore non è il numero più piccolo. (Ad esempio, quando calcoliamo 172 ÷ 4, confrontiamo 4 e 1, troviamo che 4 > 1, quindi confronta 4 con 17.)
- Scrivi la prima cifra del quoziente sopra l`ultima cifra del dividendo utilizzato per il confronto. Dopo aver confrontato 4 e 17, notiamo che 4 va in 17 quattro volte, quindi scriviamo 4 come prima cifra del nostro quoziente, sopra 7.
- Moltiplica e sottrai per trovare il resto. Moltiplica il quoziente per il divisore, in questo caso 4 x 4 = 16. Scrivi il 16 sotto il 17, poi fai 17 - 16 per il resto, 1.
- Ripetere. Ancora una volta confrontiamo il divisore 4 con la cifra successiva, 1, notiamo che 4 > 1, e "portare" spostiamo invece la cifra successiva del dividendo verso il basso per confrontare 4 con 12. 4 va in 12 tre volte senza resto, quindi possiamo scrivere 3 come cifra successiva del quoziente. La risposta è 43.

2. Crea una configurazione di divisione lunga binaria. Supponiamo di usare come esempio 10101 ÷ 11. Scrivi questa come divisione lunga, con 10101 come dividendo e 11 come divisore. Lascia spazio sopra per scrivere il quoziente e scrivi i tuoi calcoli sotto di esso.

3. Confronta il divisore con la prima cifra del dividendo. Funziona allo stesso modo della divisione lunga decimale, ma in realtà è molto più semplice in forma binaria. O non puoi dividere il numero per il divisore (0), o il divisore entra una volta (1):

4. Ora prendi il numero successivo e ripeti fino a quando non ottieni 1. Ecco i prossimi passi del nostro esempio:

5. Determina il resto. come nella divisione lunga decimale, moltiplichiamo la cifra che abbiamo appena trovato (1) per il divisore (11) e scriviamo il risultato sotto il nostro dividendo su una riga con la cifra che abbiamo appena calcolato. In forma binaria, possiamo farlo più velocemente, perché 1 x il divisore è sempre uguale al divisore:

6. Continua finché il problema non sarà risolto. Porta la cifra successiva dal dealer al resto sotto per ottenere 100. Perché 11 < 100 scrivi un 1 come cifra successiva del quoziente. Continua a risolvere il problema come prima:

7. Aggiungi un punto radix se necessario. A volte il risultato non è un numero intero. Se hai ancora un resto dopo aver utilizzato l`ultima cifra, aggiungi a ".0" al dividendo e a "." al tuo quoziente in modo da poter abbassare di un altro numero e andare avanti. Continua a farlo finché non raggiungi la precisione desiderata, quindi arrotonda la risposta. Sulla carta puoi arrotondare omettendo lo 0 oppure, se l`ultima cifra è un 1, sottrailo e aggiungi 1 all`ultima cifra. Durante la programmazione, utilizzare uno degli algoritmi di arrotondamento standard per evitare errori durante la conversione tra numeri binari e decimali.
Metodo 2 di 2: Utilizzo del metodo del complemento

1. Comprendere l`idea di base. Un modo per risolvere le divisioni, per qualsiasi base, è continuare a sottrarre il divisore dal dividendo, quindi il resto, calcolando quante volte puoi continuare a farlo prima di arrivare a un numero negativo. Ecco un esempio per la base 10, il problema 26 ÷ 7:
- 26 - 7 = 19 (1 volte sottratte)
- 19 - 7 = 12 (2 volte sottratte)
- 12 - 7 = 5 (3 volte sottratte)
- 5 - 7 = -2. Numero negativo, quindi su di nuovo. La risposta è 3 con resto di 5. Si noti che questo metodo non tiene conto delle cifre decimali.

2. Impara a sottrarre usando i complementi. Sebbene tu possa facilmente applicare il metodo sopra ai numeri binari, possiamo anche usare un metodo più efficiente, che può farti risparmiare tempo durante la programmazione delle divisioni binarie. Questo è chiamato il metodo del complemento binario. Ecco le basi, dove calcoliamo 111 - 011 (assicurati che entrambi i numeri abbiano la stessa lunghezza):

3. Combina i due concetti sopra. Ora sai come funziona il metodo di sottrazione per risolvere le divisioni e il metodo del complemento a 2 per risolvere le somme dei meno. Puoi combinare i due in un unico metodo per risolvere i problemi di divisione, utilizzando i passaggi seguenti. Se vuoi puoi provare a scoprirlo da solo prima di continuare.

4. Sottrarre il divisore dal dividendo aggiungendo il complemento a 2. Risolviamo il seguente problema: 100011 ÷ 000101. Il primo passo è risolvere 100011 - 000101, usando il metodo del complemento a 2, in modo che diventi una somma:

5. Aggiungi 1 al quoziente. In un programma per computer, questo è il punto in cui aumenti il quoziente di 1. Sulla carta, prendi una nota in un angolo da qualche parte, dove non rovinerà il resto del tuo lavoro. Ora abbiamo eseguito con successo un minimo una volta, quindi il quoziente finora è 1.

6. Ripeti sottraendo il divisore dal resto. Il risultato del nostro ultimo calcolo è il resto rimasto dopo il divisore una volta "è entrato". Continua ad aggiungere il complemento a 2 del divisore e sottraendo il riporto. Aggiungi 1 al quoziente ogni volta e continua fino a ottenere un resto uguale al tuo divisore minore:
Consigli
- Le istruzioni di incremento, decremento o stack devono essere considerate prima di applicare un calcolo binario a una serie di istruzioni macchina.
- Il metodo del complemento a 2 per la sottrazione non funziona se i numeri sono costituiti da un numero diverso di cifre. Aggiungi zeri extra al numero più piccolo per risolvere questo problema.
- Ignora la cifra con segno nei numeri binari con segno prima di eseguire il calcolo, tranne quando si cerca di capire se una risposta è positiva o negativa.
Articoli sull'argomento "Divisione di numeri binari"
Condividi sui social network:
Popolare