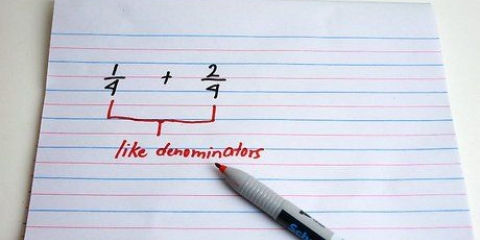
30√2 - 4√2 + 10√3 = (30 - 4)√2 + 10√3 = 26√2 + 10√3 

Semplificare 6√(40). Per prima cosa puoi dissolvere "40" in "4 x 10" e ottieni 6√(40) = 6√(4×10). Quindi calcoli `2` dal quadrato `4` e lo moltiplichi per il coefficiente corrente. Ora hai 6√(4×10) = (6 x 2)√10. Moltiplica i due coefficienti e ottieni 12√10`.` L`attività ora recita come segue: 12√10 - 3√(10) + √5. Poiché i primi due termini hanno la stessa radice, puoi sottrarre il secondo termine dal primo e lasciare il terzo così com`è. tu ami adesso (12-3)√10 + √5 circa, che può essere semplificato a 9√10 + √5. 

Perché √9 equivale √(3x3), puoi semplificare questo: √9 sta diventando 3. Perché √4 equivale √(2x2), puoi semplificare questo: √4 diventa 2. Ora la somma 3 + 2 = 5. Perché 5 e 3√2 non sono uguali, non c`è più niente da fare adesso. La tua risposta finale è 5 - 3√2. 
Assicurati che questi termini abbiano lo stesso denominatore. Il minimo comune denominatore o denominatore divisibile per `4` e `2` è `4`. Quindi, per rendere il secondo termine ((√2)/2) con denominatore 4, devi moltiplicare sia il numeratore che il denominatore per 2/2. (√2)/2 x 2/2 = (2√2)/4. Somma il denominatore delle frazioni mantenendo lo stesso denominatore. Fai solo quello che faresti se dovessi aggiungere frazioni. (√2)/4 + (2√2)/4 = 3√2)/4`.`
Aggiungi e sottrai radici quadrate
Per aggiungere e sottrarre radici quadrate, devi combinare radici quadrate con la stessa radice. Ciò significa che puoi aggiungere (o sottrarre da) 2√3 a 4√3, ma non puoi aggiungere 2√3 e 2√5. Ci sono molti casi in cui puoi semplificare il numero sotto il radicale per poter combinare termini simili e aggiungere e sottrarre liberamente le radici quadrate.
Passi
Parte 1 di 2: Padroneggiare le basi

1. Se possibile, semplifica i termini sotto i radicali. Per semplificare i termini sotto i radicali, prova a calcolarli in almeno un quadrato perfetto, come 25 (5 x 5) o 9 (3 x 3). Una volta fatto questo, puoi prendere la radice quadrata del quadrato perfetto e posizionarlo fuori dai radicali, lasciando il fattore rimanente al di sotto del radicale. In questo esempio partiamo dal problema 6√50 - 2√8 + 5√12. I numeri fuori dal radicale sono i coefficienti e i numeri sottostanti chiamiamo il numeri di radice. Ecco come semplificare i termini:
- 6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Hai sciolto `50` in `25 x 2` e poi hai posizionato `5` fuori dalla radice (la radice di `25`), dopo di che `2` rimane sotto il radicale. Quindi moltiplichi `5` per `6`, il numero che era già al di fuori del radicale, e ottieni 30 come nuovo coefficiente.
- 2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Qui hai calcolato `8` in `4 x 2` e poi hai sottratto la radice quadrata di 4 in modo da rimanere con `2` al di fuori del radicale e un `2` sotto il radicale. Quindi moltiplichi `2` per `2`, il numero che era già al di fuori del radicale, e ottieni 4 come nuovo coefficiente.
- 5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Qui hai calcolato "12" in "4 x 3" e poi hai sottratto la radice quadrata di 4 in modo da rimanere con "2" al di fuori del radicale e un "3" sotto il radicale. Quindi moltiplichi `2` per `5`, il numero che era già al di fuori del radicale, e ottieni 10 come nuovo coefficiente.

2. Cerchia tutti i termini con i numeri di radice corrispondenti. Dopo aver semplificato i numeri radice dei termini indicati, ti rimane la seguente equazione: 30√2 - 4√2 + 10√3. Dal momento che puoi solo aggiungere o sottrarre radici simili, devi cerchiare quei termini con la stessa radice, in questo esempio: 30√2 e 4√2. Puoi confrontarlo con l`aggiunta o la sottrazione di frazioni, dove puoi solo aggiungere o sottrarre i termini se i denominatori sono uguali.

3. Se stai lavorando con un`equazione più lunga e ci sono più coppie di numeri radice corrispondenti, puoi cerchiare la prima coppia, sottolineare la seconda, asterisco il terzo e così via. Mettere in ordine termini simili ti renderà più facile visualizzare la soluzione.

4. Calcola la somma dei coefficienti dei termini con radici uguali. Ora non ti resta che calcolare la somma dei coefficienti dei termini con radici uguali, ignorando gli altri termini dell`equazione. I numeri di radice rimangono invariati. L`idea è che tu indichi quanti di quel tipo di numero radice ci sono, in totale. I termini non corrispondenti possono rimanere come sono. Ecco cosa fai:
Parte 2 di 2: Più esercizio

1. Fai l`esempio 1. In questo esempio, aggiungi le seguenti radici quadrate: √(45) + 4√5. Devi fare quanto segue:
- Semplificare (45). Per prima cosa puoi slegarlo in questo modo √(9 x 5).
- Quindi prendi la radice quadrata di nove e ottieni `3`, che poi metti al di fuori della radice quadrata. Così, √(45) = 3√5.
- Ora aggiungi i coefficienti dei due termini con le radici corrispondenti per ottenere la tua risposta. 3√5 + 4√5 = 7√5

2. Fai l`esempio 2. L`esempio seguente è questo incarico: 6√(40) - 3√(10) + √5. È necessario eseguire le seguenti operazioni per risolvere questo problema:
3. Fai l`esempio 3. Questo esempio va così: 9√5 -2√3 - 4√5. Nessuna delle radici contiene un quadrato, quindi non è possibile semplificare. Il primo e il terzo termine hanno radici uguali, quindi i loro coefficienti possono essere sottratti (9 - 4). Il numero di radice rimane lo stesso. I restanti termini non sono uguali, quindi il problema può essere semplificato5√5 - 2√3`.`


4. Fai l`esempio 4. Supponiamo di avere a che fare con il seguente problema: √9 + √4 - 3√2 Ora devi fare quanto segue:

5. Fai l`esempio 5. Proviamo a prendere la somma delle radici quadrate che fanno parte di una frazione. Proprio come una frazione normale, ora puoi calcolare solo la somma delle frazioni con lo stesso numeratore o denominatore. Diciamo che stai lavorando con questo problema: (√2)/4 + (√2)/2, Ora procedi come segue:
Consigli
- I numeri di radice con un quadrato come fattore dovrebbero sempre essere semplificati per stai per determinare e combinare numeri radice uguali.
Avvertenze
- Non puoi mai combinare numeri radice disuguali.
- Non puoi mai combinare un numero intero e una radice quadrata. Così: 3 + (2x) potere non essere semplificato.
- Nota: `(2x) è uguale a `(√(2x)`.
Articoli sull'argomento "Aggiungi e sottrai radici quadrate"
Condividi sui social network:
Popolare