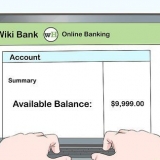
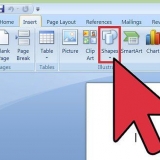
Ex. 1: √(18) x √(2) = √(36) Ex. 2: √(10) x √(5) = √(50) Ex. 3: √(3) x √(9) = √(27) 
Ex. 1: √(36) = 6. 36 è un quadrato perché è un prodotto di 6 x 6. La radice quadrata di 36 è solo 6. Ex. 2: √(50) = √(25 x 2) = √([5 x 5] x 2) = 5√(2). Mentre 50 non è un numero quadrato, 25 è un fattore 50 (perché si adatta esattamente due volte) ed è un quadrato perfetto. Puoi fattorizzare 25 (5 x 5) e inserire un 5 al di fuori del radicale per semplificare l`equazione. Puoi pensarci in questo modo: se rimetti il 5 sotto il segno radicale, si moltiplicherà da solo e diventerà di nuovo 25. Ex. 3:√(27) = 3. 27 a è un cubo perfetto (terza potenza), perché è il prodotto di 3 x 3 x 3. La radice quadrata di 27 è quindi 3. 

Ex. 1: 3√(2) x √(10) = 3√(2 x 10) = 3√(20) Ex. 2: 4√(3) x 3√(6) = 12√(3 x 6) = 12√(18) 
3√(20) = 3√(4 x 5) = 3√([2 x 2] x 5) = (3 x 2)√(5) = 6√(5) 12√(18) = 12√(9 x 2) = 12√(3 x 3 x 2) = (12 x 3)√(2) = 36√(2) 

√(5) x √(2) = ? 

--> √(5) = √(5) --> √(2) = √(2) 
√(5) = √(5 x 5) = √25 √(2) = √(2 x 2 x 2) = √8 

Moltiplica i numeri di carote insieme
Contenuto
Il simbolo della radice (√) rappresenta la radice quadrata di un numero. Potresti incontrare il simbolo della radice in matematica, o anche in falegnameria o in qualsiasi altro campo in cui entra in gioco la geometria o quando si calcolano dimensioni o distanze relative. Puoi moltiplicare le radici che hanno lo stesso potere (radici del potere). Se i radicali non hanno la stessa potenza, puoi modificare la loro equazione finché non lo fanno. Se vuoi sapere come moltiplicare le radici con o senza coefficienti, segui i passaggi seguenti.
Passi
Metodo 1 di 3: moltiplicare le radici senza coefficienti

1. Assicurati che le radici abbiano la stessa potenza. Per moltiplicare le radici usando il metodo di base, devono avere la stessa potenza. Il `potere` è il piccolo numero scritto a sinistra della riga superiore del simbolo della radice. Se non viene specificata alcuna potenza, allora hai a che fare con una radice quadrata (seconda potenza) e può essere moltiplicata per altre radici quadrate. Puoi moltiplicare insieme radici di poteri diversi, ma questo è un metodo avanzato e verrà spiegato in seguito. Ecco due esempi di moltiplicazione delle radici con gli stessi poteri:
- Ex. 1: √(18) x √(2) = ?
- Ex. 2: √(10) x √(5) = ?
- Ex. 3: √(3) x √(9) = ?

2. Moltiplica i numeri sotto il radicale. Quindi moltiplichi i numeri sotto il segno radicale e lo lasci lì. Questo va così:

3. Semplifica le radici. Dopo aver moltiplicato le radici, ci sono buone probabilità che possano essere semplificate a un quadrato perfetto oa una potenza di due, oppure possono essere semplificate trovando un quadrato come fattore del prodotto finale. Lo fai come segue:
Metodo 2 di 3: Moltiplicare le radici per coefficienti

1. Moltiplica i coefficienti. I coefficienti sono i numeri al di fuori del radicale. Se non viene fornito alcun coefficiente, puoi considerare il coefficiente come 1. Moltiplica i coefficienti insieme. Lo fai come segue: Ex. 2: 4√(3) x 3√(6) = 12√( ? ) 4 x 3 = 12
- Ex. 1: 3√(2) x √(10) = 3√( ? )
- 3 x 1 = 3

2. Moltiplica i numeri all`interno delle radici. Dopo aver moltiplicato i coefficienti, puoi iniziare a moltiplicare i numeri all`interno delle radici. Lo fai come segue:

3. Semplifica il prodotto. Quindi semplifichi i numeri sotto le radici cercando i quadrati perfetti o multipli dei numeri sotto le radici che compongono i quadrati perfetti. Dopo aver semplificato questi termini, moltiplica i loro coefficienti corrispondenti per. Lo fai come segue:
Metodo 3 di 3: Moltiplica le diverse radici del potere

1. Trova l`LCF (Least Common Multiple) delle potenze. Per trovare l`LCF delle potenze, trova il numero più piccolo divisibile per entrambe le potenze. Trova l`LCF degli indici per la seguente equazione: √(5) x √(2) = ?
- Gli indici sono 3 e 2. 6 è la LCF di questi due numeri, perché è il numero più piccolo divisibile sia per 3 che per 2. 6/3 = 2 e 6/2 = 3. Per moltiplicare le radici, entrambe le potenze devono essere 6.

2. Scrivi ogni espressione con il nuovo LCF come potenza. Le espressioni appariranno così rispetto ai loro nuovi poteri:

3. Trova il numero per il quale devi moltiplicare ciascuna delle potenze originali per determinare l`LCF. Con l`espressione √(5) la tua potenza di 3 dovrà essere moltiplicata per 2 per ottenere 6. Con l`espressione √(2) dovrai moltiplicare la potenza 2 per 3 per ottenere 6.

4. Rendi questo numero l`esponente del numero all`interno della radice quadrata. Nella prima equazione, 2 diventa la potenza di 5. Nella seconda equazione, 3 diventa la potenza di 2. Questo sarà simile a questo:

5. Moltiplica i numeri all`interno delle radici per i loro esponenti. Lo fai come segue:

6. Metti questi numeri sotto un radicale. Mettili sotto un segno radicale e collegali con un segno di moltiplicazione. Ecco come appare il risultato: √(8 x 25)

7. Moltiplicare. √(8 x 25) = √(200). Questa è la risposta finale. In alcuni casi, potresti essere in grado di semplificare ulteriormente queste espressioni, ad esempio, se riesci a trovare un numero che moltiplicato sei volte per se stesso produce 200. Ma ciò non è possibile, il che significa che l`espressione non può essere ulteriormente semplificata.
Consigli
- Se c`è un segno più o meno tra un numero e il radicale, allora non è un coefficiente, nel qual caso è un termine separato e dovrebbe essere trattato separatamente dal radicale. Se un radicale e un altro termine sono racchiusi tra parentesi, ad esempio (2 + √5), allora devi trattare sia 2 che √5 separatamente quando esegui operazioni tra parentesi, ma quando esegui operazioni fuori parentesi, devi considera (2 + √5) come un tutto.
- I segni della radice sono un altro modo per esprimere esponenti frazionari. In altre parole, la radice quadrata di un numero è la stessa di quel numero elevato alla potenza 1/2, la radice cubica di qualsiasi numero è la stessa di quel numero elevato alla potenza 1/3 e così via.
- UN "coefficiente" è il numero (se c`è un numero) immediatamente prima del radicale. Quindi nell`espressione 2√5, 5 è al di sotto del radicale e il numero 2 (al di fuori del radicale) è il coefficiente. Quando una radice e un coefficiente sono rappresentati come un gruppo, significa che la radice e il coefficiente devono essere moltiplicati tra loro, così come nell`esempio: 2 * √5.
Articoli sull'argomento "Moltiplica i numeri di carote insieme"
Condividi sui social network:
Popolare