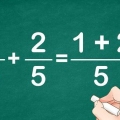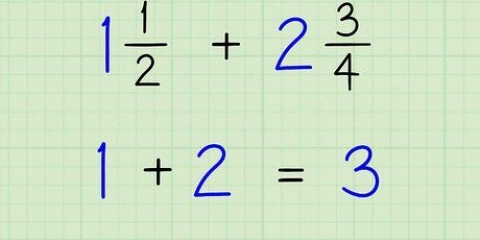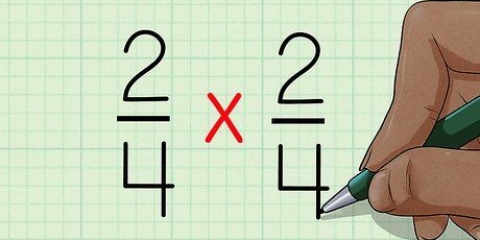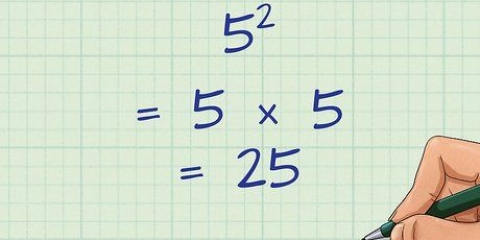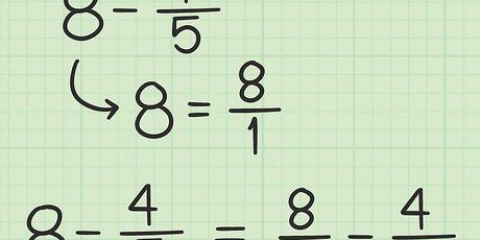Ex. 1: 1/4 + 2/4
Ex. 2: 3/8 + 2/8 + 4/8
Ex. 1: 1/4 + 2/4 è la nostra equazione. "1" e"2" sono i contatori. Ciò significa 1 + 2 = 3.
Ex. 2: 3/8 + 2/8 + 4/8 è la nostra equazione. "3" e"2" e"4" sono i contatori. Ciò significa 3 + 2 + 4 = 9.
Ex. 1: 3 è il nostro nuovo numeratore e 4 è il `nuovo` denominatore. Questo dà la risposta: 3/4. 1/4 + 2/4 = 3/4.
Ex. 2: 9 è il nostro nuovo numeratore e 8 è il `nuovo` denominatore. Questo dà la risposta: 9/8. 3/8 + 2/8 + 4/8 = 9/8.
Se il numeratore è maggiore del denominatore, come in per esempio. 2, quindi almeno un numero intero può essere rimosso dalla frazione. Dividi il numeratore per il denominatore. Se dividiamo 9 per 8, otteniamo 1 intero e resto di 1. Metti il numero intero prima della frazione e il resto come numeratore della nuova frazione, mantenendo lo stesso denominatore.9/8 = 1 1/8.

Ex. 3: 1/3 + 3/5
Ex. 4: 2/7 + 2/14
Ex. 3: 3 x 5 = 15. Entrambe le frazioni hanno 8 come denominatore.
Ex. 4: 14 è un multiplo di 7. Quindi dobbiamo solo moltiplicare 7 per 2 per ottenere 14. Entrambe le frazioni hanno quindi denominatore 14.
Ex. 3: 1/3 x 5/5 = 5/15.
Ex. 4: Per questa frazione dobbiamo solo moltiplicare la prima frazione per 2, perché in questo modo possiamo ottenere il denominatore comune.
2/7 x 2/2 = 4/14. Ex. 3: 3/5 x 3/3 = 9/15.
Ex. 4: La seconda frazione non ha bisogno di essere moltiplicata perché entrambe le frazioni hanno già lo stesso denominatore. Ex. 3: invece di 1/3 + 3/5, abbiamo 5/15 + 9/15
Ex. 4: invece di 2/7 + 2/14, abbiamo 4/14 + 2/14
Ex. 3: 5 + 9 = 14. Il 14 sarà il nuovo contatore.
Ex. 4: 4 + 2 = 6. 6 sarà il nuovo contatore.
Ex. 3: 15 sarà il nostro nuovo denominatore.
Ex. 4: 14 sarà il nostro nuovo denominatore.
Ex. 3: 14/15 è la nostra nuova risposta a 1/3 + 3/5 = ?
Ex. 4: 6/14 è la nostra risposta a 2/7 + 2/14 = ?
Ex. 3: 14/15 non può essere semplificato.
Ex. 4: 6/14 può essere ridotto a 3/7 dividendo sia il numeratore che il denominatore per 2, il massimo comune divisore.
Aggiungi le frazioni insieme
Contenuto
Essere in grado di aggiungere frazioni è un`abilità molto utile. Non solo per la scuola primaria e secondaria, è solo un`abilità molto pratica. Leggi di più sull`aggiunta di frazioni qui. Rimarrai stupito da ciò che imparerai in pochi minuti.
Passi
Metodo 1 di 2: Parte prima: sommare frazioni con lo stesso denominatore

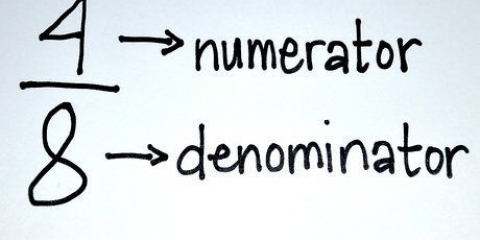
1. Controlla i denominatori (i numeri sotto la linea) di ciascuna frazione. Se hanno lo stesso numero, allora hai a che fare con frazioni con denominatori simili. In caso contrario, salta la sezione successiva.
2. Ecco due esempi di problemi su cui lavoreremo in questa sezione. Quando arrivi all`ultimo passaggio dovresti capire come funziona l`addizione.


3. Prendi i due numeratori (i numeri sopra la linea) e sommali. Non importa quante frazioni hai, se hanno lo stesso denominatore puoi semplicemente sommare tutti i numeratori insieme.


4. Costruisci la nuova frazione. Prendi la somma dei numeratori che hai ottenuto nel passaggio 2; questa somma diventa il nuovo contatore. Usa il denominatore delle frazioni del passaggio precedente. Questo sarà il nuovo denominatore; questo denominatore rimane sempre lo stesso quando si sommano frazioni con lo stesso denominatore


5. Semplifica se puoi. Semplifica la nuova frazione per assicurarti che i numeri siano il più piccoli possibile.

Metodo 2 di 2: Parte seconda: sommare frazioni con denominatori disuguali

1. Controlla i denominatori (numeri sotto la linea di frazione) di ciascuna frazione. Se i denominatori sono disuguali, devi trovare un modo per renderli uguali. Continua a leggere per sapere come.
2. Ecco due esempi di problemi su cui lavoreremo in questa sezione. Quando arriviamo all`ultimo passaggio, sai come sommare frazioni con denominatori diversi.


3. Trova un denominatore adatto. Puoi farlo cercando il multiplo comune dei denominatori. Un modo semplice per trovarlo è semplicemente moltiplicare entrambi i denominatori. Se uno dei denominatori è un multiplo dell`altro, devi solo moltiplicare l`altra frazione.


4. Moltiplica entrambi i numeri della prima frazione per il denominatore della seconda frazione. Non vi è alcun cambiamento nel valore della frazione; cambiamo solo l`aspetto della frazione. È sempre la stessa frazione.


5. Moltiplica entrambi i numeri della seconda frazione per il denominatore della prima frazione. Ancora una volta, non cambiamo il valore della frazione, ma solo come appare. È sempre la stessa frazione.

6. Metti entrambe le frazioni una accanto all`altra con i loro nuovi numeri. Non sono stati ancora sommati, solo un po` di pazienza! Quello che abbiamo fatto è moltiplicare ogni frazione per un numero appropriato, con l`obiettivo di rendere uguali entrambi i denominatori.


7. Somma i numeratori di entrambe le frazioni.


8. Prendi il denominatore uguale che hai calcolato nel passaggio 2 e usalo come denominatore della nuova frazione. A proposito, questo è ovviamente lo stesso denominatore che vedi già nella frazione modificata.




9. Semplifica la frazione. Semplifica la frazione dividendo sia il numeratore che il denominatore per il massimo comune divisore.


Consigli
Articoli sull'argomento "Aggiungi le frazioni insieme"
Condividi sui social network:
Popolare