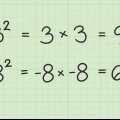Radici Quadrate Dividenti

Contenuto

Passi
Consigli
Avvertenze

La divisione per radici quadrate è essenzialmente la semplificazione di una frazione. Certo, la presenza di radici quadrate rende il processo un po` più complicato, ma ci sono regole che ci permettono di lavorare con le frazioni in modo relativamente semplice. La cosa più importante da ricordare è che devi dividere i coefficienti per i coefficienti e le radici per le radici. Inoltre, non dovresti mai lasciare una radice quadrata in un denominatore.

Passi

Metodo 1 di 4: condivisione delle carote

Immagine titolata Divide Square Roots Step 1

1. Prepara la frazione. Se l`espressione non è già in forma di frazione, riscrivila in questo modo. Questo rende più facile seguire tutti i passaggi necessari per dividere per radice quadrata. Ricorda che un carattere di divisione è uguale a una barra di frazione.

Ad esempio, se tu $\sqrt{144} \div \sqrt{36}$ ${sqrt{144}}div {sqrt{36}}$ calcola, quindi riscrivi il problema come: $\frac{\sqrt{144}}{\sqrt{36}}$ ${frac{{sqrt{144}}}{{sqrt{36}}}}$ .

Immagine titolata Divide Square Roots Step 2

2. Usa un segno radicale. Se il tuo problema ha una radice quadrata nel numeratore e nel denominatore, puoi mettere entrambe le radici sotto un radicale. (Una radice è il numero sotto il radicale.) Ciò rende la semplificazione ancora più semplice.

Ad esempio,

\frac{\sqrt{144}}{\sqrt{36}}

${frac{{sqrt{144}}}{{sqrt{36}}}}$ può essere riscritto come

\sqrt{\frac{144}{36}}

${sqrt{{frac{144}{36}}}}$ .

Immagine titolata Divide Square Roots Step 3

3. Dividi le radici. Dividi i numeri come faresti con qualsiasi intero. Assicurati di posizionare il quoziente sotto un nuovo radicale.

Ad esempio,

\frac{144}{36} = 4

${frac{144}{36}}=4$ , Così

\sqrt{\frac{144}{36}} = \sqrt{4}

${sqrt{{frac{144}{36}}}}={sqrt{4}}$ .

Immagine titolata Divide Square Roots Step 4

4. Semplificare, Se necessario. Se la radice è un quadrato, o se uno dei fattori è un quadrato perfetto, è necessario semplificare l`espressione. Un quadrato o un quadrato perfetto è il prodotto di un intero moltiplicato per se stesso. Ad esempio, 25 è un quadrato perfetto perché

5 \times 5 = 25

$5volte 5=25$ .

Ad esempio, 4 è un quadrato perfetto perché

2 \times 2 = 4

$2volte 2=4$ . Così:

\sqrt{4}

${sqrt{4}}$

= \sqrt{2 \times 2}

$={sqrt{2volte 2}}$

= 2

$=2$
così,

\frac{\sqrt{144}}{\sqrt{36}} = \sqrt{4} = 2

${frac{{sqrt{144}}}{{sqrt{36}}}}={sqrt{4}}=2$ .

Metodo 2 di 4: Fattorizzazione delle radici

Immagine titolata Divide Square Roots Step 5

1. Esprimi il problema come una frazione. Probabilmente l`espressione è già scritta in questo modo. In caso contrario, cambialo. Renderlo una frazione rende i passaggi necessari più facili da seguire, specialmente quando si calcolano le radici quadrate. Ricorda che un carattere di divisione è uguale a una barra di frazione.

Ad esempio, durante il calcolo $\sqrt{8} \div \sqrt{36}$ ${sqrt{8}}div {sqrt{36}}$ , riscrivi l`espressione come: $\frac{\sqrt{8}}{\sqrt{36}}$ ${frac{{sqrt{8}}}{{sqrt{36}}}}$ .

Immagine titolata Divide Square Roots Step 6

2. Scomponi ogni carota in fattori. Fattorizza il numero come faresti con un numero intero. Lascia i fattori sotto i segni radicali.

Ad esempio:

\frac{\sqrt{8}}{\sqrt{36}} = \frac{\sqrt{2 \times 2 \times 2}}{\sqrt{6 \times 6}}

${frac{{sqrt{8}}}{{sqrt{36}}}}={frac{{sqrt{2volte 2volte 2}}}{{sqrt{6volte 6 }}}}$

Immagine titolata Divide Square Roots Step 7

3. Semplifica numeratore e denominatore della frazione. a per semplificare una radice quadrata, escludi tutti i fattori di cui il prodotto è un quadrato?. Un quadrato è il risultato di un intero moltiplicato per se stesso. Il fattore ora diventa un coefficiente esterno alla radice quadrata.

Ad esempio:

\sqrt{} 2 \times 2 \times 2 \sqrt{6 \times 6}

${frac{{sqrt{{cancel{2times 2times }}2}}}{{sqrt{{cancel{6times 6}}}}}}}$

2 \sqrt{2} 6

${frac{2{sqrt{2}}}{6}}$
così,

\frac{\sqrt{8}}{\sqrt{36}} = 2 \sqrt{2} 6

${frac{{sqrt{8}}}{{sqrt{36}}}}={frac{2{sqrt{2}}}{6}}$

Immagine titolata Divide Square Roots Step 8

4. Eliminare il segno radicale dal denominatore, se necessario. Di norma, un`espressione non può avere una radice quadrata al denominatore. Se la tua frazione ha una radice quadrata al denominatore, devi eliminarla. Ciò significa rimuovere la radice nel denominatore. Per fare ciò, moltiplica il numeratore e il denominatore della frazione per la radice quadrata che devi eliminare.

Ad esempio, supponiamo che la tua espressione lo sia

6 \sqrt{2} \sqrt{3}

${frac{6{sqrt{2}}}{{sqrt{3}}}}$ , quindi devi moltiplicare numeratore e denominatore per

\sqrt{3}

${sqrt{3}}$ per rimuovere la radice quadrata dal denominatore:

6 \sqrt{2} \sqrt{3} \times \frac{\sqrt{3}}{\sqrt{3}}

${frac{6{sqrt{2}}}{{sqrt{3}}}}times {frac{{sqrt{3}}}{{sqrt{3}}}}$

= 6 \sqrt{2} \times \sqrt{3} \sqrt{3} \times \sqrt{3}

$={frac{6{sqrt{2}}times {sqrt{3}}}{{sqrt{3}}times {sqrt{3}}}}$

= 6 \sqrt{6} \sqrt{9}

$={frac{6{sqrt{6}}}{{sqrt{9}}}}$

= 6 \sqrt{6} 3

$={frac{6{sqrt{6}}}{3}}$ .

Immagine titolata Divide Square Roots Step 9

5. Semplifica ulteriormente, se necessario. A volte ti rimangono coefficienti che possono essere ulteriormente semplificati, o ridurre. Semplifica gli interi nel numeratore e nel denominatore proprio come semplificheresti una frazione.

Ad esempio,

\frac{2}{6}

${frac{2}{6}}$ può essere ridotto a

\frac{1}{3}

${frac{1}{3}}$ , Così

2 \sqrt{2} 6

${frac{2{sqrt{2}}}{6}}$ può essere ridotto a

1 \sqrt{2} 3

${frac{1{sqrt{2}}}{3}}$ , o semplicemente

\frac{\sqrt{2}}{3}

${frac{{sqrt{2}}}{3}}$ .

Metodo 3 di 4: Dividere le radici quadrate con i coefficienti

Immagine titolata Divide Square Roots Step 10

1. Semplifica i coefficienti. Questi sono i numeri fuori dal radicale. Per semplificarli, condividi o ridurre, ignora le radici quadrate per ora.

Ad esempio, se tu $4 \sqrt{32} 6 \sqrt{16}$ ${frac{4{sqrt{32}}}{6{sqrt{16}}}}$ devi calcolare, poi semplifichi prima $\frac{4}{6}$ ${frac{4}{6}}$ . Il numeratore e il denominatore possono essere divisi entrambi per un fattore 2. Quindi puoi semplificarlo in: $\frac{4}{6} = \frac{2}{3}$ ${frac{4}{6}}={frac{2}{3}}$ .

Immagine titolata Divide Square Roots Step 11

2. Semplifica le radici quadrate. Se il numeratore è divisibile per il denominatore, basta dividere i numeri sotto i radicali. In caso contrario, semplifica ogni radice quadrata allo stesso modo delle altre radici quadrate.

Ad esempio, poiché 32 è divisibile per 16, puoi dividere le radici quadrate:

\sqrt{\frac{32}{16}} = \sqrt{2}

${sqrt{{frac{32}{16}}}}={sqrt{2}}$ .

Immagine titolata Divide Square Roots Step 12

3. Moltiplica i coefficienti semplificati per la radice quadrata semplificata. Ricorda che non può esserci una radice quadrata in un denominatore, quindi quando moltiplichi una frazione per una radice quadrata, metti la radice quadrata nel numeratore.

Ad esempio,

\frac{2}{3} \times \sqrt{2} = 2 \sqrt{2} 3

${frac{2}{3}}times {sqrt{2}}={frac{2{sqrt{2}}}{3}}$ .

Immagine titolata Divide Square Roots Step 13

4. Eliminare la radice quadrata al denominatore, se necessario. Questa si chiama razionalizzazione del denominatore. La regola è che un`espressione non può avere una radice quadrata al denominatore. Per sottrarre la radice dal denominatore, moltiplica il numeratore e il denominatore per la radice quadrata che vuoi sottrarre.

Ad esempio, se hai un`espressione come

4 \sqrt{3} 2 \sqrt{7}

${frac{4{sqrt{3}}}{2{sqrt{7}}}}$ , quindi devi moltiplicare numeratore e denominatore per

\sqrt{7}

${sqrt{7}}$ per eliminare la radice quadrata al denominatore:

4 \sqrt{3} \sqrt{7} \times \frac{\sqrt{7}}{\sqrt{7}}

${frac{4{sqrt{3}}}{{sqrt{7}}}}times {frac{{sqrt{7}}}{{sqrt{7}}}}$

= 4 \sqrt{3} \times \sqrt{7} \sqrt{7} \times \sqrt{7}

$={frac{4{sqrt{3}}times {sqrt{7}}}{{sqrt{7}}times {sqrt{7}}}}$

= 4 \sqrt{21} \sqrt{49}

$={frac{4{sqrt{21}}}{{sqrt{49}}}}$

= 4 \sqrt{21} 7

$={frac{4{sqrt{21}}}{7}}$

Metodo 4 di 4: Dividere per un binomio con radice quadrata

Immagine titolata Divide Square Roots Step 14

1. Determina se hai un binomio al denominatore. Il denominatore è il numero del problema per cui stai dividendo. Un binomio è un polinomio con due termini. Questo metodo si applica solo alla divisione di radici quadrate che coinvolgono un binomio.

Ad esempio, se tu $1 5 + \sqrt{2}$ ${frac{1}{5+{sqrt{2}}}}$ Se vuoi calcolare, hai un binomio al denominatore, perché $5 + \sqrt{2}$ $5+{sqrt{2}}$ è un polinomio con due termini.

Immagine titolata Divide Square Roots Step 15

2. Determina la congiunzione del binomio. Le coppie coniugate sono binomi con gli stessi termini ma operatori opposti. Usando una coppia di congiuntivi puoi eliminare la radice quadrata dal denominatore.

Ad esempio,

5 + \sqrt{2}

$5+{sqrt{2}}$ e

5 - \sqrt{2}

$5-{sqrt{2}}$ sono coppie congiuntive, perché hanno gli stessi termini, ma operatori opposti.

Immagine titolata Divide Square Roots Step 16

3. Moltiplica numeratore e denominatore per la congiunzione del denominatore. Questo permette di eliminare la radice quadrata, perché il prodotto di una coppia coniugata è la differenza del quadrato di ogni termine nel binomio. Questo è,

(un - B) (un + B) = un 2 - B^{2}

$(a-b)(a+b)=a^{{2}}-b^{{2}}$ .

Ad esempio:

1 5 + \sqrt{2}

${frac{1}{5+{sqrt{2}}}}$

= 1 (5 - \sqrt{2}) (5 + \sqrt{2}) (5 - \sqrt{2})

$={frac{1(5-{sqrt{2}})}{(5+{sqrt{2}})(5-{sqrt{2}})}}$

= 5 - \sqrt{2} (5 2 - (\sqrt{2})^{2}

$={frac{5-{sqrt{2}}}{(5^{{2}}-({sqrt{2}})^{{2}}}}$

= 5 + \sqrt{2} 25 - 2

$={frac{5+{sqrt{2}}}{25-2}}$

= 5 + \sqrt{2} 23

$={frac{5+{sqrt{2}}}{23}}$
così,

1 5 + \sqrt{2} = 5 + \sqrt{2} 23

${frac{1}{5+{sqrt{2}}}}={frac{5+{sqrt{2}}}{23}}$ .

Consigli

Molte calcolatrici hanno funzioni speciali per le frazioni. Immettere il coefficiente del numeratore, premere il pulsante delle frazioni, quindi immettere il coefficiente del denominatore. Quando si preme il segno di uguale in seguito, la calcolatrice dovrebbe aver riscritto i coefficienti nei minimi termini.
A differenza di addizione e sottrazione di radici, in una frazione non è necessario semplificare prima le radici per rimuovere i quadrati. In effetti, spesso è meglio non farlo.
Se lavori con radici quadrate, le frazioni improprie sono più facili da risolvere rispetto ai numeri misti.

Avvertenze

Non mettere mai un decimale in una frazione. Altrimenti sarebbe una frazione all`interno di una frazione.
Non anteporre mai un numero decimale o misto a una radice, convertirlo in una frazione e semplificare l`intera espressione.
Non lasciare mai una radice quadrata al denominatore di una frazione, ma semplificare la frazione.
Se il denominatore contiene una qualche forma di addizione o sottrazione, utilizzare il metodo della coppia coniugata per rimuovere il radicale dal denominatore.