Questo processo è sostanzialmente lo stesso che calcolare prima l`area della base e poi moltiplicare quest`area per l`altezza del cubo (o in altre parole lunghezza × larghezza × altezza), perché l`area della base è determinata moltiplicando la lunghezza per la larghezza. Poiché la lunghezza, la larghezza e l`altezza di un cubo sono uguali, possiamo semplificare il processo elevando uno di questi valori alla terza potenza. Continuiamo con il nostro esempio. La lunghezza del bordo era di 2 cm, quindi il volume del cubo è 2 x 2 x 2 (o 2)= 8. 
Nel nostro esempio, la lunghezza della nervatura è stata data in centimetri, quindi la risposta deve essere indicata in centimetri cubi. Quindi la risposta è 8 cm. 

Quindi nel nostro esempio dividiamo cinquanta per sei: 50/6 = 8,33 cm. Ricorda che le unità delle risposte bidimensionali si scrivono al quadrato (cm, m e così via). 
Nel nostro esempio, √8.33 = 2,89 cm. 
Quindi nel nostro esempio: 2,89 × 2,89 × 2,89 = 24,14 cm. Non dimenticare di scrivere la risposta in unità cubiche. 

Questo può essere dedotto anche dal teorema di Pitagora. D, D e l formare un triangolo equilatero con D come ipotenusa, quindi D = D + l. In precedenza avevamo già determinato: D = 2l, quindi possiamo anche dire quanto segue: D = 2l + l = 3l. Supponiamo di sapere che la lunghezza della diagonale che va da un angolo nella base del cubo all`angolo opposto nella faccia superiore del cubo è di 10 metri. Quindi, se vogliamo calcolare il volume, inseriamo 10 nella formula sopra per D. D = 3l. 10 = 3l. 100 = 3l 33.33 = l 5.77 m = l. Da questo punto possiamo calcolare il volume alzando la lunghezza della nervatura al cubo. 5.77 = 192.45 m
Calcolo del volume di un cubo
Contenuto
Un cubo è una figura tridimensionale la cui lunghezza, larghezza e altezza sono uguali. Un cubo ha sei facce quadrate, i cui lati sono di uguale lunghezza e perpendicolari tra loro. Calcolare il volume di un cubo è molto semplice, di solito basta moltiplicare quanto segue: lunghezza × larghezza × altezza. Poiché i bordi di un cubo hanno tutti la stessa lunghezza, puoi anche vedere il volume di un cubo come segue: l, per cui l è la lunghezza di uno dei bordi del cubo. Vai al passaggio 1 per una spiegazione dettagliata.
Passi
Metodo 1 di 3: Alzare il bordo del cubo fino al cubo

1. Trova la lunghezza di uno dei bordi del cubo. Spesso vedrai una somma in cui è già data la lunghezza di una delle costole. Una volta che hai queste informazioni, hai tutto il necessario per determinare il volume del cubo. Usa un righello o un metro a nastro se non stai risolvendo un problema di matematica, ma vuoi solo conoscere il volume di un oggetto a forma di cubo esistente.
- Per comprendere meglio il processo di determinazione del volume di un cubo, iniziamo con una somma di esempio mentre seguiamo i passaggi in questa sezione. Supponiamo che il bordo del cubo 2 cm lungo è. Utilizzeremo queste informazioni nel passaggio successivo per determinare il volume del cubo.

2. Alza la lunghezza della costola alla terza potenza. Una volta che hai la lunghezza di una delle costole, aumenta questo numero alla terza potenza. In altre parole, moltiplica il numero due volte per se stesso. Se l è la lunghezza della nervatura, quindi moltiplichi l × l × l (o in forma più semplice l). Il risultato è il volume del cubo.

3. Esprimi la tua risposta in unità cubiche. Il volume è la misura di uno spazio tridimensionale, quindi la soluzione deve essere scritta in unità cubiche. In un test, può costarti punti se non dichiari correttamente la risposta in unità cubiche, quindi non dimenticare!
Metodo 2 di 3: Determinazione del volume in base alla superficie

1. Trova l`area delle facce del tuo cubo. Il più facile il modo per determinare il volume è alzare la nervatura al cubo, ma non è il qualunque modo. La lunghezza del bordo di un cubo o l`area di una delle sue facce può essere derivata da diverse altre proprietà del cubo, il che significa che se inizi con queste informazioni puoi determinare il volume del cubo in modo derivato. Ad esempio, se conosci solo l`area totale di tutti i lati del cubo, puoi trovare il volume dividendo quest`area per sei e quindi prendendo la radice quadrata di quel numero per trovare la lunghezza del bordo. Da quel punto puoi salire di nuovo alla terza potenza. In questa sezione esamineremo questo processo passo dopo passo.
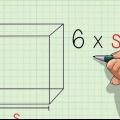
- L`area di un cubo è data dalla formula 6l, per cui l è la lunghezza di uno dei bordi del cubo. Questa formula è in realtà la stessa che determina l`area bidimensionale di uno dei lati del cubo e quindi aggiunge le sei aree (uguali). Useremo questa formula per determinare il volume del cubo dall`area del cubo.
- Supponiamo di avere un cubo di cui sappiamo che l`area 50 cm è, ma non sappiamo quale sia la lunghezza delle costole. Nei prossimi passi utilizzeremo queste informazioni per trovare il volume del cubo.

2. Dividi l`area del cubo per sei. Poiché il cubo ha sei facce di uguale area, possiamo determinare l`area di una faccia dividendo l`area del cubo per sei. L`area di un piano è la stessa della moltiplicazione di due spigoli (l × b, b × h o h × l).

3. Trova la radice quadrata di questo valore. Poiché l`area di una delle facce di un cubo è uguale a l (l × l), possiamo ora prendere la radice quadrata del valore trovato per determinare la lunghezza di una delle nervature. Una volta che lo sai, hai abbastanza informazioni per calcolare il volume del cubo come al solito.

4. Aumenta questo numero alla terza potenza per trovare il volume del cubo. Ora che hai determinato un valore per la lunghezza delle nervature, puoi aumentare questo numero al cubo per determinare il volume come descritto nella prima sezione di questo articolo.
Metodo 3 di 3: Determinazione del volume usando le diagonali

1. Dividi la diagonale di una delle facce del cubo per √2 per trovare la lunghezza dei bordi del cubo. La diagonale di un quadrato è √2 × la lunghezza di uno dei suoi bordi. In altre parole, se conosci solo il valore di una delle diagonali di una faccia del cubo, puoi calcolare la lunghezza degli spigoli del cubo dividendo questo valore per √2. Da quel punto è possibile aumentare nuovamente alla terza potenza e determinare il volume come descritto sopra.
- Supponiamo che una delle facce del cubo abbia una diagonale di7 metri lungo. Quindi possiamo calcolare la lunghezza di una delle nervature dividendo 7 per √2. 7/√2 = 4,96 metri. Ora che conosciamo la lunghezza dei bordi del cubo, possiamo calcolare il volume del cubo elevando 4,96 al cubo: 4,96 = 122,36 metri.
- Fai attenzione: D = 2l, vero D è la lunghezza della diagonale di una delle facce del cubo e l è la lunghezza di uno dei bordi del cubo. Questo può essere derivato dal teorema di Pitagora, dove il quadrato dell`ipotenusa di un triangolo equilatero è uguale alla somma del quadrato degli altri due lati. Poiché la diagonale di una faccia di un cubo forma un triangolo equilatero con due dei bordi di quella faccia, possiamo dire quanto segue: D = l + l = 2l.

2. Trova il quadrato della diagonale tra due angoli opposti del cubo, dividi per tre e prendi la radice quadrata per trovare la lunghezza di uno degli spigoli. Se la lunghezza della linea tridimensionale tra due angoli opposti del cubo è l`unica data, puoi comunque determinare il volume del cubo. D forma uno dei lati di un triangolo equilatero la cui ipotenusa è la linea tra due angoli opposti del cubo, quindi possiamo dire: D = 3l, dove D è la linea tridimensionale tra due angoli opposti del cubo.
Articoli sull'argomento "Calcolo del volume di un cubo"
Condividi sui social network:
Simile
Popolare