Nell`esempio sopra, sarebbe simile a questo: 
Nell`esempio sopra, lo calcoli come segue:
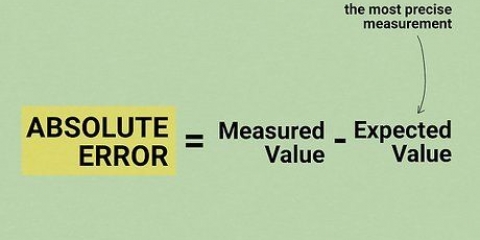
Questa equazione fornisce la deviazione al quadrato totale delle letture dalla media campionaria. Nota che il segno della differenza non ha importanza. 
Nell`esempio sopra hai 5 letture, quindi n – 1 = 4. Il tuo calcolo va così: 
Nell`esempio sopra, si calcola la deviazione standard come segue:
Quindi la deviazione standard è 0,0071624. 
Calcolo dell'errore standard
Contenuto
"Errore standard" si riferisce alla deviazione standard della distribuzione campionaria dei dati statistici. In altre parole, questo può essere utilizzato per calcolare l`accuratezza di una media campionaria. In molti casi, quando si utilizza l`errore standard, si assume implicitamente una distribuzione normale. Se vuoi calcolare l`errore standard, continua a leggere al passaggio 1.
Passi
Parte 1 di 3: Le basi

1. La deviazione standard. La deviazione standard di un campione indica il grado di diffusione dei numeri. La deviazione standard di un campione è solitamente indicata da una s. La formula matematica per la deviazione standard è mostrata sopra.

2. La popolazione significa. La media della popolazione è la media di un insieme di dati numerici che contiene tutti i valori dell`intero gruppo, in altre parole, la media di un insieme completo di numeri, piuttosto che un campione.

3. La media aritmetica. Questa è solo una media: la somma di un numero di valori, divisa per lo stesso numero di valori.

4. Riconoscere i mezzi di campionamento. Quando una media aritmetica si basa su una serie di osservazioni ottenute campionando una popolazione statistica, si parla di "media campionaria"."Questa è la media di un insieme numerico di dati in cui sono contenuti alcuni dei valori all`interno di un gruppo. Viene indicato come:

5. La distribuzione normale. La distribuzione normale, la più comunemente usata di tutte le distribuzioni, è simmetrica, con un valore anomalo alla media dei dati. La forma del grafico è quella di un orologio, con la pendenza uguale su entrambi i lati della parte superiore. Il cinquanta percento della distribuzione è a sinistra e il cinquanta percento a destra. La distribuzione di una distribuzione normale è determinata dalla deviazione standard.

6. La formula standard. La formula per l`errore standard di una media campionaria è data sopra.
Parte 2 di 3: Calcolo della deviazione standard

1. Calcola la media campionaria. Per determinare l`errore standard dovrai prima calcolare la deviazione standard (perché la deviazione standard, s, fa parte della formula per l`errore standard). Inizia calcolando la media dei valori del campione. La media campionaria è espressa come media aritmetica delle misure x1, x2, . . . xn. Questo è calcolato con la formula sopra.
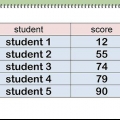
- Si supponga ad esempio di dover calcolare l`errore standard di una media campionaria per le misurazioni del peso di cinque monete, come riportato nella tabella seguente:
Calcoleresti quindi la media campionaria inserendo i valori di peso nella formula, in questo modo:

2. Sottrarre la media campionaria da ciascuna misurazione e quadrare questo valore. Una volta ottenuta la media campionaria, è possibile espandere la tabella sottraendola da ogni singola misura, quindi quadrando il risultato.

3. Determina la deviazione totale delle tue letture dalla media campionaria. La deviazione totale è la media della differenza al quadrato dalla media campionaria. Aggiungi tutti i valori insieme per determinarlo.
Questa equazione fornisce la deviazione al quadrato totale delle letture dalla media campionaria. Nota che il segno della differenza non ha importanza.

4. Calcolare la deviazione media al quadrato delle misurazioni dalla media campionaria. Una volta che conosci la deviazione totale, puoi trovare la deviazione media usando n -1. Si noti che n è uguale al numero di misurazioni.

5. Determina la deviazione standard. Ora hai tutti i valori necessari per utilizzare la formula della deviazione standard.
Quindi la deviazione standard è 0,0071624.
Parte 3 di 3: Determinazione dell`errore standard

1. Utilizzare la deviazione standard per calcolare l`errore standard con la formula standard.
- Nell`esempio sopra, si calcola l`errore standard come segue:
Quindi l`errore standard (la deviazione standard della media campionaria) è 0,0032031 grammi.
Consigli
- L`errore standard e la deviazione standard sono spesso confusi. Si noti che l`errore standard è una descrizione della deviazione standard della distribuzione campionaria di un valore statistico, non la distribuzione dei singoli valori.
- Nelle riviste scientifiche, l`errore standard e la deviazione standard sono talvolta usati in modo intercambiabile. Un segno ± viene utilizzato per unire le due letture.
Articoli sull'argomento "Calcolo dell'errore standard"
Condividi sui social network:
Simile
Popolare