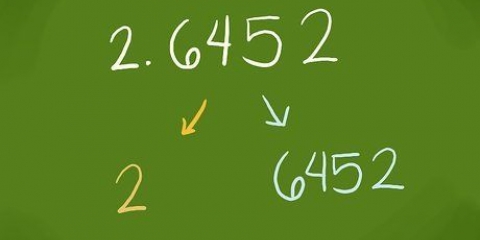Calcolo dell'Emivita di una Sostanza: 8 Passaggi (con Immagini)

Contenuto

Passi
- Parte 1 di 2: Calcolo dell`emivita
- Parte 2 di 2: risoluzione dei problemi di emivita
Avvertenze
Necessità

L`emivita o l`emivita di una sostanza che decade nel tempo è il tempo impiegato da una data quantità di quella sostanza per decadere della metà. In linea di principio, questo termine era riservato al decadimento radioattivo di elementi come l`uranio o il plutonio, ma può essere utilizzato anche per qualsiasi sostanza soggetta a decadimento, a velocità lineare o esponenziale. È possibile calcolare l`emivita di qualsiasi sostanza, a condizione che venga indicato il tasso di decadimento. Questa è la quantità della sostanza con cui inizi e la quantità che rimane dopo un certo tempo. Continua a leggere per imparare a calcolare l`emivita di una sostanza.

Passi

Parte 1 di 2: Calcolo dell`emivita

Immagine titolata Calculate Half Life Step 1

1. Dividere la quantità di una sostanza in un dato momento per la quantità rimasta dopo un certo periodo di tempo.

La formula per calcolare l`emivita è la seguente: T_1/2 = t * ln(2)/ln(N₀/N_T)
In questa formula vediamo le seguenti variabili: t = tempo trascorso, N₀ = quantità di una sostanza per la misurazione e N_T = quantità di una sostanza dopo un certo periodo di tempo.
Ad esempio, se l`importo iniziale è 1500 grammi e l`importo finale è 1000 grammi, allora 1500 / 1000 = 1,5. Diciamo che il tempo trascorso è pari a (t) = 100 minuti.

Immagine titolata Calculate Half Life Step 2

2. Calcola il logaritmo (log) del numero del passaggio precedente. Tutto quello che devi fare ora è digitare log(1,5) sulla calcolatrice.

Il log di un numero con una data base è l`esponente di cui la base viene incrementata (o il numero di volte che la base viene moltiplicata per se stessa) per ottenere quel numero. Il registro ha base 10. Il pulsante di registro sulla calcolatrice è un logaritmo regolare.

Se calcoli quel log (1.5) = 0.176, dam significa che il log di 1.5 è uguale a 0.176. Ciò significa ancora una volta che 10 alla potenza di 0,176 è uguale a 1,5.

Immagine titolata Calculate Half Life Step 3

3. Moltiplica il tempo trascorso per log(2). Registro(2) = 0,30103. Il tempo trascorso è di 100 minuti.

Ad esempio, se il tempo trascorso è pari a 100 minuti, moltiplicare 100 per 0,30103. Questo risultato è pari a 30.103.

Immagine titolata Calculate Half Life Step 4

4. Dividi il risultato del calcolo precedente per il numero del secondo passaggio.

Quindi, 30,103 / 0,176 = 171,04. Questa è l`emivita della sostanza espressa nell`unità di tempo del terzo passaggio.

Immagine titolata Calculate Half Life Step 5

5. Finito. Ora che hai trovato l`emivita di questo esempio, è bene sapere che avresti potuto usare il logaritmo naturale (ln) invece del log normale per ottenere lo stesso risultato. In effetti, il logaritmo naturale è usato più spesso per trovare l`emivita rispetto al log ordinario.

Quindi,ln( 1.5) = 0.405 e ln(2) = 0.693. Quindi segue: 0,693 x 100 = 69,3. Dividi questo numero per 0,405 e ottieni 171,04, la stessa risposta del log normale.

Parte 2 di 2: risoluzione dei problemi di emivita

1. Determina la quantità di una sostanza con un`emivita nota rimane dopo un determinato numero di giorni. Risolvere: Se a un paziente vengono somministrati 20 mg di iodio-131, quanto ne rimane dopo 32 giorni? L`emivita dello iodio-131 è di 8 giorni. Ecco cosa fare:

Determina quanta sostanza viene dimezzata in 32 giorni. Per fare ciò, dividi 32 per 8 (emivita della sostanza). 32/8 = 4, quindi il tessuto viene dimezzato 4 volte.
Ciò significa che dopo 8 giorni hai ancora 20 mg/2 o 10 mg della sostanza; dopo 16 giorni è ancora 10 mg/2 o 5 mg; dopo 24 giorni rimangono 5 mg/2 o 2,5 mg e dopo 32 giorni rimangono ancora 2,5 mg/2 o 1,25 mg della sostanza.

2. Determinare l`emivita di una determinata sostanza, conoscendo la quantità iniziale e finale, nonché il tempo trascorso. Risolvi il seguente problema: Se un laboratorio riceve una spedizione di 200 g di tecnezio-99 m e rimangono solo 12,5 g dell`isotopo, qual è l`emivita del tecnezio-99 m? Ecco cosa fare:

Risolvi questo davanti a dietro. Se rimanevano 12,5 grammi di sostanza, prima del dimezzamento c`erano 25 g di sostanza (12,5 x 2); prima c`erano 50 g di sostanza; di nuovo per 100 g e hai iniziato con 200 g.

Quindi la sostanza doveva essere dimezzata 4 volte per arrivare da 200 g a 12,5 g, quindi si può calcolare che l`emivita è pari a 24 ore/4 = 6 ore.

3. La domanda è quanti dimezzamenti sono necessari per ridurre una sostanza a una certa quantità. Risolvi quanto segue: Se l`emivita dell`uranio-232 è di 70 anni, quanti dimezzamenti sono necessari per ridurre 20 g della sostanza a 1,25 g? Ecco l`effetto:

Inizia con 20 g e riduci. 20/2 = 10 (1 halving), 10/2 = 5 (2 halving), 5/2 = 2,5 (3 halving) e 2,5/2 = 1,25 (4 halving). La risposta è 4 metà.

Avvertenze

L`emivita è una stima (per caso) del tempo necessario affinché metà della sostanza lasciata decadere, piuttosto che un calcolo esatto. Ad esempio, se è rimasto un solo atomo di una certa sostanza, il dimezzamento non è più possibile (o rimangono 1 o 0 atomi). Maggiore è la quantità del residuo, più accurato è il calcolo dell`emivita, perché hai a che fare con la legge dei grandi numeri.