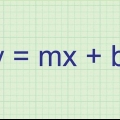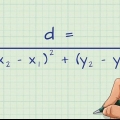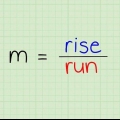Usare la Formula della Pendenza

Contenuto

Passi
Consigli

La formula della pendenza è un modo comune per scrivere un`equazione lineare. Questa formula è scritta come "y = mx + b" – dove alle lettere viene assegnato un certo valore per poter risolvere questa equazione, oppure dove si risolve l`equazione per trovare i valori delle variabili. Così: "X" e "y" sono i "X-" e "y"-coordinate di una linea, "m" è la pendenza (pendenza), il rapporto (cambiamento di y)/(cambiamento di x) e "B" è l`intersezione con l`asse y. Se vuoi sapere come utilizzare la formula della pendenza, sei nel posto giusto.

Passi

Metodo 1 di 5: utilizzare la formula della pendenza per i problemi

Immagine titolata Use the Slope Intercept Form (in Algebra) Passaggio 1

1. Leggi il compito. Prima di poter procedere, devi leggere attentamente il compito in modo da capire esattamente cosa ti viene chiesto. Leggi la seguente dichiarazione: Il tuo conto in banca aumenta linearmente ogni settimana. Se hai $ 560 sul tuo conto bancario dopo 20 settimane di lavoro e $ 585 dopo 21 settimane, come esprimi il rapporto tra l`importo che hai guadagnato e quante settimane hai lavorato utilizzando la formula della pendenza.

Immagine titolata Use the Slope Intercept Form (in Algebra) Step 2

2. Pensa al problema in termini di formula della pendenza. Dovresti scriverlo così: y = mx + b. La variabile "m" è la pendenza e "B" è il punto iniziale in cui la linea interseca l`asse y. Si noti che il problema afferma che, " Il tuo conto in banca aumenta linearmente ogni settimana," il che significa che risparmi lo stesso importo ogni settimana, il che a sua volta significa che hai una linea retta e inclinata. Quella "costante," e un piano di risparmio uniformemente continuo è ciò che lo rende lineare. Se non risparmi ogni volta lo stesso importo, non è lineare.

Immagine titolata Use the Slope Intercept Form (in Algebra) Step 3

3. Trovare la pendenza della linea. Per trovare la pendenza devi essere in grado di determinare il tasso di variazione. Se inizi con 560€ e la settimana successiva hai 585€, hai guadagnato 25€ dopo 1 settimana di lavoro. Puoi anche calcolarlo sottraendo € 560 da € 585. 585-560 = 25.

4. Trova l`intersezione con l`asse y. Per trovare questo incrocio, chiamato anche il "B" in y = mx + b, devi conoscere il punto di partenza del tuo problema (che è l`intersezione con l`asse y). Ciò significa che devi scoprire con quanti soldi hai iniziato. Se avevi $ 560 dopo 20 settimane di lavoro e sai di aver guadagnato $ 25 in una settimana, usa la seguente moltiplicazione per calcolare quanto hai guadagnato in 20 settimane. 20 x 25 = 500, quindi hai guadagnato $ 500 in quelle settimane.

Perché dopo 20 settimane hai 560€ e guadagni anche 500€. allora sai quanto hai iniziato sottraendo 500 da 560. 560 - 500 = 60.

Così il "B" o il punto di partenza, è 60.

5. Scrivi l`equazione. Ora che conosci la pendenza, m è 25 (guadagnando 25 dollari a settimana) e il punto di partenza b è 60, puoi inserirlo nell`equazione:

y = mx + b

y = 25x + 60

6. Verifica se l`equazione è corretta. Il "y" è la quantità di denaro che hai guadagnato e il "X" il numero di settimane in cui hai lavorato. Scopri quanti soldi hai guadagnato in un determinato numero di settimane inserendo questi dati nell`equazione. Prova due esempi:

Quanti soldi hai guadagnato in 10 settimane? riempire "10" dentro per il "X" per scoprirlo qui.

y = 25x + 60 =

y = 25(10) + 60 =

y = 250 + 60 =

y = 310. Dopo 10 settimane hai guadagnato € 310.

Quante settimane devi lavorare per guadagnare 800 euro? riempire "800" dentro per il "y"-variabile dell`equazione per ottenere il valore di "X" venire.

y = 25x + 60 =

800 = 25x + 60 =

800 - 60 =

25x = 740 =

25x/25 = 740/25 =

x = 29.6. Puoi guadagnare 800 euro in circa 30 settimane.

Metodo 2 di 5: Conversione di un`equazione nella formula della pendenza

1. Scrivi l`equazione. Supponiamo di avere a che fare con la seguente equazione, 4 anni +3 volte = 16.

2. Isola il termine y su un lato dell`equazione. Puoi farlo sottraendo 3x da entrambi i lati dell`equazione. L`equazione dovrebbe ora apparire così: 4y = -3x +16.

4 anni + 3 volte = 16

4 anni + 3 volte - 3 volte = 16 -3 volte

4 anni = -3x +16

3. Dividi tutti i termini per il coefficiente di y. Questo è il numero della variabile y. Non mettere un numero qui, allora hai finito. Se esiste un numero (il coefficiente), dividi ogni termine nell`equazione per quel numero. In questo caso, il coefficiente y è 4, quindi devi dividere 4x, -3x e 16 per 4 per ottenere la risposta finale. Ecco come funziona:

4 anni = -3x +16 =

/₄y = /₄X +/_{4 = (per divisione)}

y = /₄X + 4 (semplificando la divisione)

4. Determina i termini nell`equazione. Quando usi l`equazione per disegnare una linea, ricordalo "y" la coordinata y è en "-3/4" il pendio o il pendio, "X" è quindi le coordinate x e "4" l`intersezione con l`asse y.

Metodo 3 di 5: La formula della pendenza utilizzando un punto e la pendenza

1. Scrivi l`equazione della retta come formula della pendenza. Basta scrivere prima y = mx + b. È quindi possibile compilare l`equazione una volta che si dispone di dati sufficienti. Supponiamo di voler risolvere il seguente problema: Trova l`equazione di una retta con pendenza 4 passante per il punto (-1, -6).

2. Compila i dettagli. Lo sai "m" è uguale alla pendenza della linea, è uguale a 4 e quello "y" e "X" rispettivamente il "X" e "y" le coordinate sono. In questo caso, i dati sono "X" = -1 e "y" = -6. "B" rappresenta l`intersezione con l`asse y; questo valore non è ancora noto. Ecco come appare ora l`equazione:

y = -6, m = 4, x = -1 (i valori dati)

y = mx + b (la formula)

-6 = (4)(-1) + b (dopo la compilazione)

3. Risolvere per "B". Ora si tratta di allenarsi "B," trova l`intersezione con l`asse y. Moltiplica 4 e -1 quindi sottrai il risultato da -6. Ecco come farlo:

-6 = (4)(-1) + b

-6 = -4 + b

-6 - (-4) = -4 -(-4) + b

-6 - (-4) = b (termine semplificato a destra)

-2 = b (termine a sinistra semplificato)

4. Scrivi l`equazione. Ora tu "B," puoi inserire i valori necessari nella formula della pendenza. Tutto quello che devi sapere è la pendenza e l`intersezione con l`asse y (b):

m = 4, b = -2

y = mx + b

y = 4x -2 (sostituzione)

Metodo 4 di 5: annotare la formula della pendenza utilizzando due punti

1. Scrivi i due punti. Prima di poter fare l`equazione della retta, scrivi i due punti che ti vengono dati. Supponiamo di voler risolvere il seguente problema: Trova l`equazione della retta passante per i punti (-2, 4) e (1, 2).

2. Usa questi punti per trovare la pendenza dell`equazione. La formula per determinare la pendenza della retta passante per due punti è (y₂ - y₁) / (X₂ - X₁). Hai a che fare con le coordinate (x₁, Y₁) = (-2, 4) e (x₂, Y₂ ) = (1, 2). Ora inserisci questo valore nell`equazione e risolvi per m.

(s₂ - y₁) / (X₂ - X₁) =

(2 - 4)/(1 - -2) =

-2/3 = m

La pendenza della linea è -2/3.

3. Scegli uno dei punti da risolvere per l`intersezione con l`asse y. Non importa quale coppia scegli. Scegli quello con cui è più facile lavorare. Supponiamo di scegliere il punto (1, 2). Ora inserisci questo nell`equazione "y = mx + b". Risolvere per "B":

y = 2, x, = 1, m = -2/3

y = mx + b

2 = (-2/3)(1) + b

2 = -2/3 + b

2 - (-2/3) = b

2 + 2/3 = b, o b = /₃

4. Compilando i numeri nell`equazione originale. Ora che sai che la pendenza è uguale a 2/3 e l`intersezione con l`asse y ("B") è uguale a 2 2/3, puoi inserire questi valori nell`equazione originale della linea e il gioco è fatto.

y = mx + b

y = /₃X + 2 2/3

Metodo 5 di 5: tracciare la linea

1. Scrivi l`equazione e usala per tracciare la linea. Supponiamo di avere la seguente equazione: y = 4x + 3.

2. Inizia con l`intersezione con l`asse y. L`intersezione con l`asse y è data da "+3" o "B" nell`equazione. Questo è il punto (0, 3). Indica questo punto con un punto.

3. Usa la pendenza della linea per trovare le coordinate dell`altro punto. Perché sai che la pendenza è rappresentata da "m=4," puoi dire che la pendenza è uguale a y/x=4/1. Ciò significa che ogni volta che la linea sale di 4 punti sull`asse y, si sposta di 1 punto a destra sull`asse x. Quindi, inizi dal punto (0, 3) e sali di 4 punti e 1 punto a destra, finendo al punto (1, 7) come punto successivo della linea.

Se la pendenza è negativa, la linea scende da sinistra a destra.

4. Collega i due punti con una linea. Usa una matita e un righello per questo. Questo è tutto ciò che devi fare e hai tracciato una linea perfetta secondo l`equazione data. Due punti sono sufficienti per tracciare la linea. Se necessario, verifica disegnando qualche punto in più.

Consigli

Un esempio di diminuzione e aumento lineare è il cambiamento costante della velocità di un oggetto, misurata in metri al secondo, distanza misurata nel tempo.
L`algebra è attiva. Non devi solo leggere e capire la teoria, devi anche lavorare con essa per capire come funziona.
Questo è il vero modo per farti capire: Il cambiamento di y rispetto al cambiamento di x è chiamato aumento (crescita) o diminuzione (decremento) della differenza di y divisa per la differenza di x. La divisione per è anche chiamata rapporto, frazione o rapporto. Ecco il rapporto "il grado di cambiamento.
All`inizio, elabora anche i semplici esercizi su carta. Se lavorerai su esercizi più difficili in una fase successiva, trarrai molto beneficio da questo metodo perché ti dà un`idea migliore della procedura da seguire per fare un grafico.
Ricorda: la moltiplicazione viene prima dell`addizione, quindi y = mx + b; quindi prima m ×x e poi x+b.
Non limitarti a leggere gli esempi. Annotali ed esercitati nei diversi passaggi in modo da comprendere bene l`intero processo.
Impressionerai sicuramente il tuo insegnante se impari a capire come applicare un`equazione lineare a tutti i tipi di problemi.
Il sistema di coordinate cartesiane utilizzato in algebra per creare un grafico, ecc. prende il nome dal suo inventore francese, che lo usava per le coordinate sulle mappe. Sistemi simili sono utilizzati in varie aree della matematica, nonché in astronomia, navigazione, schermi di computer, insegne al neon e tabelloni segnapunti o per localizzare quasi tutto.
La pendenza di una linea misura il rapporto tra la variazione verticale (y) e la variazione orizzontale (x). Può trattarsi di punti su una linea, ma anche di un certo tasso di crescita lineare o del pendio di una collina.