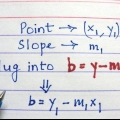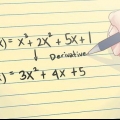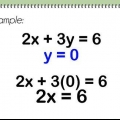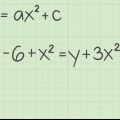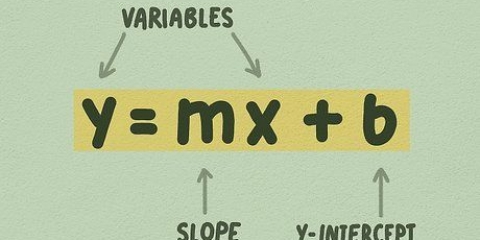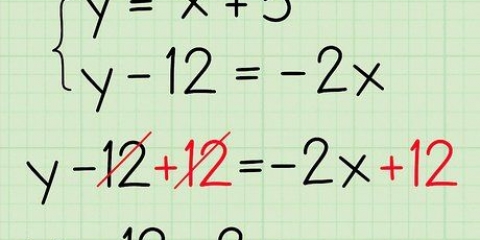Trova l'Intersezione di un'Equazione con l'Asse Y

Contenuto

Passi
Consigli

L`intercetta y di un`equazione è il punto in cui il grafico di un`equazione si interseca con l`asse y. Esistono diversi modi per trovare questo incrocio, a seconda delle informazioni fornite all`inizio del comando.

Passi

Metodo 1 di 3: trovare l`intersezione con l`asse y, utilizzando la pendenza

Immagine titolata Find the Y Intercept Step 1

1. Nota la pendenza. La pendenza di `y su x` è un singolo numero che indica la pendenza di una linea. Questo tipo di problema ti dà anche il (x,y)-coordinata di un punto del grafico. Se non disponi di entrambi questi dettagli, continua con gli altri metodi di seguito.

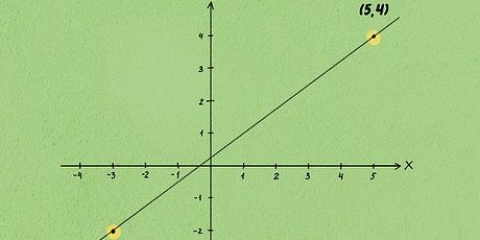
Esempio 1: Una retta con pendenza 2 passa per il punto (-3,4). Determina l`intersezione con l`asse y di questa linea utilizzando i passaggi seguenti.

Immagine titolata Find the Y Intercept Step 2

2. Impara la forma usuale di un`equazione lineare. Qualsiasi linea retta può essere scritta come y = mx + b. Quando l`equazione è in questa forma, è m la pendenza e la costante B l`intersezione con l`asse y.

Immagine titolata Find the Y Intercept Step 3

3. Sostituisci la pendenza in questa equazione. Annota l`equazione lineare, ma invece di m usi la pendenza della tua linea.

Esempio 1 (continua):y = mx + b
m = pendenza = 2
y = 2x + b

Immagine titolata Find the Y Intercept Step 4

4. Sostituisci xey con le coordinate del punto. Se hai le coordinate di un punto sulla linea, puoi X e y-coordinate sostitutive per il X e y nella tua equazione lineare. Fallo per confrontare il tuo compito.

Esempio 1 (continua): Il punto (3,4) è su questa linea. a questo punto, x = 3 e y = 4.
Sostituisci questi valori in y = 2X +B:
4 = 2(3) + b

Immagine titolata Find the Y Intercept Step 5

5. Risolvere per B. Non dimenticare, B è l`intersezione con l`asse y della retta. Ora B è l`unica variabile nell`equazione, riordina l`equazione da risolvere per questa variabile e trova la risposta.

Esempio 1 (continua):4 = 2(3) + b
4 = 6 + b
4 - 6 = b
-2 = b
L`intersezione di questa linea con l`asse y è -2.

Immagine titolata Find the Y Intercept Step 6

6. Scrivilo come una coordinata. L`intersezione con l`asse y è il punto in cui la linea si interseca con l`asse y. Poiché l`asse y passa per il punto x = 0, la coordinata x dell`intersezione con l`asse y è sempre 0.

Esempio 1 (continua): L`intersezione con l`asse y è a y = -2, quindi il punto di coordinate è (0, -2).

Metodo 2 di 3: utilizzo di due punti

Immagine titolata Find the Y Intercept Step 7

1. Annotare le coordinate di entrambi i punti. Questo metodo affronta problemi in cui sono dati solo due punti su una retta. Scrivi ciascuna coordinata nella forma (x,y).

Immagine titolata Find the Y Intercept Step 8

2. Esempio 2: Una linea retta passa attraverso i punti (1, 2) e (3, -4). Determina l`intersezione con l`asse y di questa linea utilizzando i passaggi seguenti.

Immagine titolata Find the Y Intercept Step 9

3. Calcola i valori x e y. La pendenza o pendenza è una misura di quanto la linea si sposta in direzione verticale per ogni gradino in direzione orizzontale. Potresti conoscerlo come `y su x` (

\frac{y}{X}

${frac{y}{x}}$ ). Ecco come determinare questi valori utilizzando due punti:

Il cambiamento di `y` è il cambiamento nella direzione verticale, o la differenza tra il y-valori dei due punti.

Il cambiamento di `x` è il cambiamento nella direzione orizzontale, o la differenza tra il X-valori dei due punti.

Esempio 2 (continua): I valori y dei due punti sono 2 e -4, quindi la linea aumenta in direzione verticale con (-4) - (2) = -6.
I valori x dei due punti (nello stesso ordine) sono 1 e 3, quindi la linea aumenta orizzontalmente di 3 - 1 = 2.

Immagine titolata Find the Y Intercept Step 10

4. Dividi y per x per determinare la pendenza. Ora che conosci questi due valori, puoi usarli in `

\frac{y}{X}

${frac{y}{x}}$ ` per determinare la pendenza della linea.

Esempio 2 (continua):

S l o P e = \frac{y}{X} = - 6 2 =

$pendenza={frac{y}{x}}={frac{-6}{2}}=$ -3.

Immagine titolata Find the Y Intercept Step 11

5. Dai un`altra occhiata alla forma standard di un`equazione lineare. Puoi descrivere una retta con la formula y = mx + b, per cui m la pendenza è e B l`intersezione con l`asse y. Ora che abbiamo la pendenza m e un punto (x,y), possiamo usare questa equazione per trovare B da risolvere (l`intersezione con l`asse y).

Immagine titolata Find the Y Intercept Step 12

6. Inserisci la pendenza e il punto nell`equazione. Prendi l`equazione in forma standard e sostituiscila m dalla pendenza che hai calcolato. Sostituisci le variabili X e y dalle coordinate di un singolo punto della retta. Non importa quale punto usi.

Esempio 2 (continua): y = mx + b
Pendenza = m = -3, quindi y = -3x + b
La retta passa per un punto con coordinate (x,y) (1,2), quindi 2 = -3(1) + b.

Immagine titolata Find the Y Intercept Step 13

7. Risolvi per b. Ora l`unica variabile rimasta nell`equazione è B, l`intersezione con l`asse y. Riordina l`equazione in modo che B da un lato dell`equazione e hai la tua risposta. Ricorda che l`intersezione con l`asse y ha sempre una coordinata x di 0.

Esempio 2 (continua): 2 = -3(1) + b
2 = -3 + b
5 = b
L`intersezione con l`asse y è (0,5).

Metodo 3 di 3: Utilizzo di un`equazione

Immagine titolata Find the Y Intercept Step 14

1. Scrivi l`equazione della retta. Se hai l`equazione della retta, puoi determinare l`intersezione con l`asse y con un po` di algebra.

Esempio 3: Qual è l`intersezione con l`asse y della linea x + 4y = 16?
Nota: l`esempio 3 è una linea retta. Vedere la fine di questa sezione per un esempio di equazione quadratica (usando una variabile elevata alla potenza di 2).

Immagine titolata Find the Y Intercept Step 15

2. Sostituisci 0 con x. L`asse y è una linea verticale passante per x = 0. Ciò significa che qualsiasi punto sull`asse y ha una coordinata x di 0, inclusa l`intersezione della linea con l`asse y. Immettere 0 per x nell`equazione.

Esempio 3 (continua): x + 4y = 16
x = 0
0 + 4 anni = 16
4 anni = 16

Immagine titolata Find the Y Intercept Step 16

3. Risolvi per y. La risposta è l`intersezione della linea con l`asse y.

Esempio 3 (continua): 4 anni = 16

4 y 4 = \frac{16}{4}

${frac{4y}{4}}={frac{16}{4}}$
y = 4.
L`intersezione della linea con l`asse y è 4.

Immagine titolata Find the Y Intercept Step 17

4. Confermalo disegnando un grafico (opzionale). Controlla la tua risposta rappresentando graficamente l`equazione nel modo più accurato possibile. Il punto in cui la linea passa per l`asse y è l`intersezione con l`asse y.

Immagine titolata Find the Y Intercept Step 18

5. Trova l`intersezione con l`asse y di un`equazione quadratica. Un`equazione quadratica ha una variabile (x o y) elevata alla seconda potenza. Usando la stessa sostituzione, puoi risolvere per y, ma poiché l`equazione quadratica è una curva, può intersecare l`asse y in 0, 1 o 2 punti. Ciò significa che ti ritroverai con 0, 1 o 2 risposte.

Esempio 4: Per trovare l`intersezione di

y 2 = X + 1

$y^{2}=x+1$ con l`asse y, sostituisci x = 0 e risolvere l`equazione quadratica.
In questo caso possiamo

y 2 = 0 + 1

$y^{2}=0+1$ risolvere prendendo la radice quadrata di entrambi i membri. Ricorda che ottieni due risposte quando prendi una radice quadrata: una risposta negativa e una positiva.

\sqrt{y} 2 = \sqrt{1}

${sqrt{y^{2}}}={sqrt{1}}$
y = 1 o y = -1. Queste sono entrambe intersezioni con l`asse y di questa curva.

Consigli

Alcuni paesi usano a C o qualsiasi altra variabile per B nell`equazione y = mx + b. Il suo significato, tuttavia, rimane lo stesso; è solo una notazione diversa.
Per equazioni più complicate, puoi usare i termini con y isolare su un lato dell`equazione.
Quando si calcola la pendenza tra due punti, è possibile X e y-sottrai le coordinate in qualsiasi ordine, purché metti il punto nello stesso ordine sia per y che per x. Ad esempio, la pendenza tra (1, 12) e (3, 7) può essere calcolata in due modi diversi:

Secondo punto – primo punto: $7 - 12 3 - 1 = - 5 2 = - 2.5$ ${frac{7-12}{3-1}}={frac{-5}{2}}=-2.5$
Primo punto – secondo punto: $12 - 7 1 - 3 = 5 - 2 = - 2.5$ ${frac{12-7}{1-3}}={frac{5}{-2}}=-2.5$