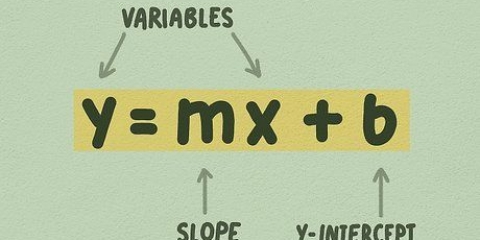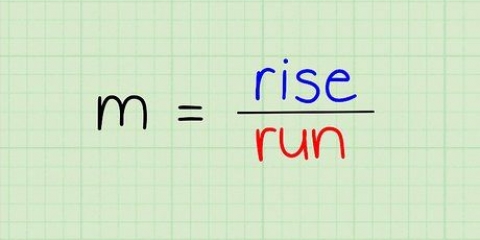Sono dati un punto e una pendenza. Vengono forniti due punti, ma nessuna pendenza. Dati un punto e un`altra retta ad esso parallela. Dati un punto e un`altra retta ad esso perpendicolare. 




Riordina la tua equazione. b = y - mx. Inserisci i valori e risolvi. b = -5 - (2/3)6. b = -5 - 4. b = -9 Verifica che l`intersezione con l`asse y sia effettivamente -9. Scrivi l`equazione: y = 2/3 x - 9 

Usa la tua pendenza e le coordinate nell`equazione sopra. Moltiplica la pendenza (m) con la coordinata x del punto. Sottrarre il valore dalla coordinata y del punto. ora hai B risolto, l`intersezione con l`asse y. 



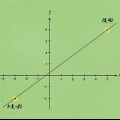
Calcola la pendenza. La pendenza = (Y2 - Y1) / (X2 - X1) -12 - (-5) / 8 - 6 = -7 / 2 La pendenza è -7/2 (dal primo punto al secondo andiamo 7 in basso e 2 a destra, quindi la pendenza è -7 su 2). Riordina la tua equazione. b = y - mx. Inserisci i valori e risolvi. b = -12 - (-7/2)8. b = -12 - (-28). b = -12 + 28. b = 16 Nota: poiché abbiamo usato l`8 per le coordinate, dobbiamo usare anche il -12.Se usi il 6 per le tue coordinate, devi usare anche il -5. Verifica che la tua intersezione con l`asse y sia realmente 16. Scrivi l`equazione: y = -7/2 x + 16 
Sostituisci la pendenza e le coordinate nell`equazione precedente. Moltiplica la pendenza (m) con la coordinata x del punto. Sottrarre il valore dalla coordinata y del punto. Hai B risolto, l`intersezione con l`asse y. 


Risolvi il pendio. La pendenza della nostra nuova linea sarà la stessa della pendenza della vecchia linea. Determina la pendenza della vecchia linea: -2 anni = -5x + 1 tiro "-2" fuori da entrambi i lati: y = 5/2x - 1/2 La pendenza è 5/2. Riordina la tua equazione. b = y - mx. Compila e risolvi. b = 3 - (5/2)4. b = 3 - (10). b = -7. Controlla se l`intersezione con l`asse y è davvero -7. Scrivi l`equazione: y = 5/2 x - 7 
2/3 diventa -3/2 -6/5 diventa 5/6 3 (o 3/1 — è lo stesso) diventa -1/3 -1/2 diventa 2 
Inserisci la tua pendenza e le coordinate nell`equazione sopra. Moltiplica la pendenza (m) con la coordinata x del punto. Sottrarre quel valore dalla coordinata y del punto. Ora hai risolto l`equazione per B; l`intersezione con l`asse y. 


Risolvi il pendio. La pendenza della nostra nuova linea diventa l`inverso negativo della pendenza della vecchia linea. Determina la pendenza della vecchia linea: 2 anni = -4x + 9 tiro "2" fuori da entrambi i lati: y = -4/2x + 9/2 La pendenza è -4/2 o -2. Il reciproco negativo di -2 è 1/2. riordina la tua equazione. b = y - mx. Compila e risolvi. b = -1 - (1/2)8. b = -1 - (4). b = -5. Verifica che la tua intersezione con l`asse y sia davvero -5. Scrivi l`equazione: y = 1/2 x - 5
Trovare l'equazione di una retta
Contenuto
Per trovare l`equazione di una retta che hai servono due cose:a) un punto della retta; e b) la pendenza (a volte anche la pendenza) della linea. Ma il modo in cui raccogli queste due informazioni e cosa ne fai in seguito può essere molto diverso a seconda della situazione. Per semplicità, questo articolo si concentrerà sulle equazioni della forma y = mx + b invece di (y - y1) = m(x - x1).
Passi
Metodo 1 di 5: Informazioni generali
1. Sapere cosa cercare.Prima di poter cercare il confronto, devi sapere con certezza cosa stai cercando di trovare. Tieni a mente quanto segue:
- I punti sono classificati come coppia ordinata, come (-7, -8) o (-2,-6).
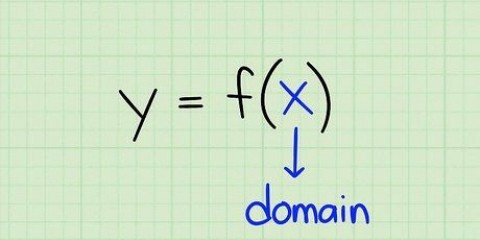
- Il primo numero di una coppia ordinata è il coordinata x. Questa è la posizione orizzontale del punto (quante unità a sinistra oa destra dell`origine).
- Il secondo numero in una coppia ordinata è il coordinare. Questa è la posizione verticale del punto (quante unità in alto o in basso dall`origine).
- Il pendenza tra i due punti si chiama il "la discesa" — in altre parole, quanto devi andare su (o giù) e destra (o sinistra) per andare da un punto all`altro.
- Due linee sono parallelo se non si intersecano.
- Due righe sono perpendicolari tra loro se si intersecano ad angolo retto (90 gradi).
2. Determina con quale tipo di incarico hai a che fare.
3. Affronta il problema utilizzando uno dei quattro metodi seguenti. A seconda delle informazioni fornite, ci sono diversi modi per risolverlo.
Metodo 2 di 5: Vengono forniti un punto e una pendenza

1. Trova l`intersezione della tua equazione con l`asse y. L`intersezione con l`asse y (o la variabile B nella nostra equazione) è il punto in cui la linea si interseca con l`asse y. È possibile calcolare l`intersezione con l`asse y riorganizzando l`equazione da risolvere B. La nostra nuova equazione ora si presenta così: b = y - mx.
- Inserisci la tua pendenza e le coordinate nell`equazione sopra.
- Moltiplica la pendenza (m) con la coordinata x del punto.
- Sottrarre quel valore dalla coordinata y del punto.
- Ora hai B risolto, l`intersezione con l`asse y.

2. Scrivi la formula:y = ____ x + ____ , insieme agli spazi vuoti.

3. Riempi il primo spazio vuoto, quello per la x, con la pendenza.

4. Completa il secondo spazio vuoto con l`intersezione con l`asse y che hai calcolato prima.

5. Risolvi il problema di esempio. "Dato il punto (6, -5) e la pendenza 2/3, qual è l`equazione della retta?"
Metodo 3 di 5: Vengono assegnati due punti
1. Calcola la pendenza tra due punti. Il pendio è anche chiamato il pendenza e puoi pensare a questo come alla velocità con cui qualcosa si muove lungo un asse y e un asse x immaginari. L`equazione per la pendenza è: (Y2 - Y1) / (X2 - X1)
- Prendi i due punti e usali nell`equazione (due coordinate significano due y-valori e due X-i valori). Non importa quali coordinate inserisci per prime, purché tu lo faccia in modo coerente. Qualche esempio:
- Punti (3, 8) e (7, 12). (Y2 - Y1) / (X2 - X1) = 12 - 8 / 7 - 3 = 4/4 o 1.
- Punti (5, 5) e (9, 2). (Y2 - Y1) / (X2 - X1) = 2 - 5 / 9 - 5 = -3/4.

2. Scegli un insieme di coordinate per il resto del problema. Cancella o copri l`altro set di coordinate in modo da non utilizzarle accidentalmente.

3. Calcola l`intersezione con l`asse y della tua equazione. Di nuovo, riordina la formula y = mx + b per ottenere un`equazione della forma b = y – mx. È sempre la stessa equazione; l`hai appena riorganizzato.

4. Scrivi la formula:y = ____ x + ____ , inclusi gli spazi vuoti.

5. Riempi il primo spazio vuoto, quello per la x, con la pendenza.

6. Completa il secondo spazio vuoto con l`intersezione con l`asse y.

7. Risolvi il problema di esempio. "Dati i punti (6, -5) e (8, -12), qual è l`equazione della retta?"
Metodo 4 di 5: Quando vengono forniti un punto e una retta parallela
1. Determina la pendenza della retta parallela. Ricorda che la pendenza è il coefficiente di X per cui y non ha coefficiente.
- In un`equazione come y = 3/4 x + 7, la pendenza è 3/4.
- In un`equazione come y = 3x - 2, la pendenza è 3.
- In un`equazione come y = 3x, la pendenza è ancora 3.
- In un`equazione come y = 7, la pendenza è zero (perché ci sono zero x nel problema).
- In un`equazione come y = x - 7, la pendenza è 1.
- In un`equazione come -3x + 4y = 8, la pendenza è 3/4.
- Per trovare la pendenza di un`equazione come questa, basta riorganizzarla in modo che il y è isolato:
- 4 anni = 3 volte + 8
- Dividi entrambi i lati per 4: y = 3/4x + 2

2. Calcola l`intersezione con l`asse y, usando la pendenza del primo passaggio e l`equazione b = y - mx.

3. Scrivi la formula:y = ____ x + ____ , con gli spazi vuoti.

4. Riempi il primo spazio vuoto, prima della x, con la pendenza determinata nel passaggio 1.La cosa notevole delle linee parallele è che hanno la stessa pendenza, quindi finisci con quello con cui hai iniziato.

5. Riempi l`intersezione con l`asse y nel secondo spazio vuoto.
6. Risolvi il problema di esempio. "Dati il punto (4, 3) e la parallela 5x - 2y = 1; qual è l`equazione della retta?"
Metodo 5 di 5: Con un punto dato e una retta perpendicolare
1. Trova la pendenza della retta data. Dai un`occhiata agli esempi sopra per ulteriori informazioni.

2. Trova il reciproco negativo di quella pendenza. In altre parole, giralo e cambia il segno. Il punto con le linee perpendicolari è che hanno una pendenza inversa negativa, quindi dovrai apportare modifiche alla pendenza prima di poterla utilizzare.

3. Calcolare l`intersezione con l`asse y utilizzando la pendenza dal passaggio 2 e l`equazione b = y - mx

4. Scrivi la formula:y = ____ x + ____ , con gli spazi vuoti.

5. Riempi il primo spazio vuoto, prima della x, con la pendenza calcolata nel passaggio 2.

6. Riempi l`intersezione con l`asse y nel secondo spazio vuoto.
7. Risolvi il problema di esempio. "Data (8, -1) e e la perpendicolare 4x + 2y = 9; qual è l`equazione della retta?"
Articoli sull'argomento "Trovare l'equazione di una retta"
Condividi sui social network:
Simile
Popolare