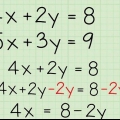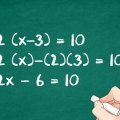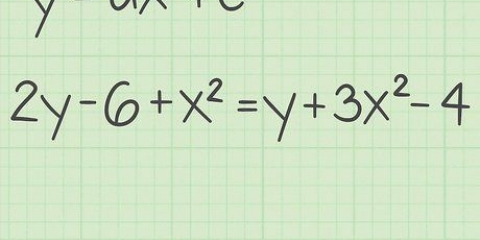Ad esempio, supponiamo di avere l`equazione 3X + -2X + 14X=0. Da a X fuori parentesi, otteniamo X(3X + -2X + 14)=0. 
Nella nostra dichiarazione di esempio inseriamo i nostri valori a, b e C (rispettivamente 3, -2 e 14) nell`equazione quadratica in: Risposta 1: Risposta 2: 
Il motivo per cui funziona ha a che fare con il fatto fondamentale che qualsiasi numero moltiplicato per zero è uguale a zero. Quando si converte l`equazione nel modulo X(ascia + bx + C)=0, essenzialmente dividi i due in parti: una parte è il X-variabile all`esterno delle parentesi e l`altro è il quadrato all`interno delle parentesi. Se una di queste parti è uguale a zero, lo è anche l`intera equazione. Quindi se le due risposte al quadrato tra parentesi rendono quella parte zero, anche le risposte all`equazione cubica renderanno uguale a zero la parte fuori dalle parentesi. 

Nella nostra dichiarazione di esempio, un=2 e d=6. I fattori di 2 sono 1 e 2. I fattori di 6 sono 1, 2, 3 e 6. 
Nella nostra equazione calcoli i fattori di un (1, 2) sui fattori di D (1, 2, 3, 6) e ottieni il seguente elenco: 1, 1/2, 1/3, 1/6, 2 e 2/3. Ora aggiungiamo i numeri negativi all`elenco per renderlo completo: 1, -1, 1/2, -1/2, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3 e -2/3. La soluzione intera della nostra equazione cubica può essere trovata da qualche parte in questo elenco. 
La condivisione sintetica è un argomento complesso: segui il link sopra per ulteriori informazioni. Ecco un esempio di come trovare una delle soluzioni della nostra equazione cubica usando la divisione sintetica: 

Nel nostro problema di esempio, lo risolviamo come segue: 
Nel nostro problema di esempio, lo risolviamo come segue: 
Nel nostro problema di esempio, determinare Δ è molto semplice, perché sia Δ0 che Δ1=0. Risolviamo questo come segue: 
Nel nostro problema di esempio, troviamo C come segue: 
Nel nostro problema di esempio, possiamo risolverlo controllando la risposta quando n è uguale a 1, 2 o 3. Le risposte che otteniamo da questi test sono le possibili risposte alla nostra equazione cubica: qualsiasi soluzione che restituisce 0 dopo la sostituzione nell`equazione è corretta. Ad esempio, supponiamo di ottenere 1 in risposta a uno dei test, perché inserendo 1 in X - 3X + 3X - 1 risulta in 0 se la risposta, allora 1 una delle risposte alla nostra equazione cubica.
Risolvere un'equazione cubica
Contenuto
La prima volta che incontri un`equazione cubica (della forma ascia + bx + cx + D=0) potrebbe sembrare quasi irrisolvibile. Tuttavia, questo metodo per risolvere le equazioni cubiche esiste da secoli! Fu scoperto nel XVI secolo dai matematici italiani Niccolò Tartaglia e Gerolamo Cardano. Fu una delle prime formule sconosciute agli antichi greci e romani. Risolvere equazioni cubiche può essere molto difficile, ma con il giusto approccio (e sufficienti conoscenze di base), anche le equazioni cubiche più complicate possono essere domate.
Passi
Metodo 1 di 3: risolverlo con la formula abc

1. Controlla se l`equazione cubica contiene una costante. Come indicato sopra, le equazioni cubiche hanno la forma ascia + bx + cx + D=0. avanti Cristo, e D può essere 0 senza cambiare se si tratta o meno di un`equazione cubica, il che significa essenzialmente che un`equazione non deve essere composta da tutti i termini bx, cx o D essere un`equazione cubica. Inizi ad applicare questo metodo relativamente semplice per risolvere le equazioni cubiche controllando prima se la tua equazione ha una costante (a D-dove la). È questo non è il caso, allora puoi de formula abc per trovare le risposte dell`equazione con un po` di matematica.
- Se l`equazione contiene una costante, dovrai utilizzare un metodo diverso. Vedi sotto per approcci alternativi.

2. sciogliere a X fuori dall`equazione. Poiché la tua equazione non contiene una costante, ogni termine nell`equazione ha a X-variabile. Ciò significa che a X può essere scomposto dall`equazione per semplificarla. Fallo e riscrivi la tua equazione nel modulo X(ascia + bx + C).

3. Usa la formula abc per risolvere i termini tra parentesi. Potresti aver notato che i termini della tua nuova equazione tra parentesi hanno la forma di un`equazione quadratica (ascia + bx + C). Ciò significa che possiamo trovare i valori per i quali l`equazione quadratica è uguale a zero di a, b e C nella formula abc ({-B +/-√ (B- 4AC)}/2un). Questo troverà due delle risposte della tua equazione cubica.
- {-B +/-√ (B- 4AC)}/2un
- {-(-2) +/-√ ((-2)-4(3)(14))}/2(3)
- {2 +/-√ (4 - (12)(14))}/6
- {2 +/-√ (4 - (168)}/6
- {2 +/-√ (-164)}/6
- {2 + √(-164)}/6
- {2 + 12.8io}/6
- {2 - 12.8io}/6

4. Usa zero e le risposte quadratiche come risposte alla tua equazione cubica. Le equazioni quadrilatere hanno due soluzioni, ma le equazioni cubiche ne hanno tre. Ne hai già due: queste sono le risposte che hai trovato elaborando l `"equazione quadratica" tra parentesi. Nei casi in cui un`equazione è appropriata per questo "fuori parentesi", la terza risposta sarà sempre 0 sono. Congratulazioni, hai appena risolto un`equazione cubica.
Metodo 2 di 3: Risolvere utilizzando elenchi di fattori

1. Assicurati che la tua equazione cubica abbia una costante. Sebbene il metodo sopra sia utile perché non richiede l`apprendimento di nuove abilità matematiche, non funzionerà sempre per risolvere equazioni cubiche. Se la tua equazione è nella forma ascia + bx + cx + D=0 stato, e D è diverso da zero, le parentesi non funzioneranno e avrai bisogno di questo metodo o di quello nella parte successiva.
- Ad esempio, supponiamo di avere l`equazione 2 dataX + 9X + 13X=-6. In questo caso, uno 0 a destra del segno di uguale richiederà l`aggiunta di 6 su entrambi i lati. La nostra nuova equazione è 2X + 9X + 13X + 6=0, D=6, quindi non possiamo usare le parentesi della parte precedente.

2. Determina i fattori di un e D. Per risolvere l`equazione cubica, inizia determinando i fattori di un (il coefficiente del X termini D (la costante alla fine dell`equazione). Come promemoria, i fattori sono quei numeri che moltiplicati insieme formano un altro numero. Ad esempio, perché il tuo 6 deriva dalla moltiplicazione 6 &volta; 1 e 2 × 3, sono 1, 2, 3 e 6 fattori di 6.

3. Condividi i fattori di un dai fattori di D. Ora elenchi tutti i valori che ottieni dividendo ogni fattore un da qualsiasi fattore D. Questo di solito si traduce in molte frazioni e pochi numeri interi. Le soluzioni intere della tua equazione cubica saranno uno degli interi dell`elenco o il numero negativo di uno di questi numeri.

4. Usa la condivisione sintetica per controllare manualmente le tue risposte. Una volta compilato l`elenco dei valori, puoi trovare le soluzioni intere per la tua equazione cubica inserendo rapidamente manualmente ogni intero e controllando quali sono uguali a zero. Se non vuoi perdere tempo su questo, c`è un metodo leggermente più veloce secondo una tecnica chiamata condivisione sintetica. Il succo è che dividi gli interi per l`originale a, b, c e D coefficienti della tua equazione cubica. Se ti rimane un resto di 0, il tuo valore è una delle soluzioni dell`equazione cubica.
- -1 | 2 9 13 6
- __| -2-7-6
- __| 2 7 6 0
- Dato che finiamo con uno 0 come resto, sappiamo che una delle soluzioni della nostra equazione cubica è l`intero -1 è.
Metodo 3 di 3: utilizzare il "discriminante"

1. Scrivi i valori di a, b, c e D. In questo metodo per trovare le soluzioni di un`equazione cubica, faremo molto affidamento sui coefficienti dei termini nella nostra equazione. Per questo motivo, è saggio usare i termini a, b, c e D scrivilo prima di iniziare in modo da non dimenticare cosa sono ciascuno.
- Ad esempio, per il confronto X - 3X + 3X - 1, scriviamo un=1, B=-3, C=3 e D=-1. Non dimenticare quello di a X-variabile senza coefficiente si assume che il coefficiente sia uguale a 1.

2. Calcola Δ0=B - 3AC. Quando usi il discriminante per risolvere le equazioni cubiche, hai bisogno di un po` di matematica più avanzata, ma se segui attentamente la procedura, scoprirai che è uno strumento prezioso per risolvere quelle già complicate equazioni cubiche. Inizia trovando Δ0, il primo di diversi valori importanti di cui abbiamo bisogno, sostituendo i valori appropriati nella formula B - 3AC.
- B - 3AC
- (-3) - 3(1)(3)
- 9 - 3(1)(3)
- 9 - 9=0=Δ0

3. Calcola Δ1=2B - 9ABC + 27unD. La prossima quantità importante di cui abbiamo bisogno, Δ1, richiede un po` più di lavoro, ma può essere trovata più o meno allo stesso modo di Δ0. Sostituisci i valori corretti nella formula 2B - 9ABC + 27unD per il valore di Δ1.
- 2(-3) - 9(1)(-3)(3) + 27(1)(-1)
- 2(-27) - 9(-9) + 27(-1)
- -54 + 81 - 27
- 81 - 81=0=Δ1

4. Calcola Δ=Δ1 - 4Δ0) ÷ -27un. Quindi calcoliamo il discriminante dell`equazione cubica dai valori per Δ0 e Δ1. Un discriminante è semplicemente un numero che ci dice qualcosa sulle risposte di un polinomio (inconsciamente potresti già conoscere il discriminante quadratico: B - 4AC). Nel caso dell`equazione cubica, se il discriminante è positivo, allora l`equazione ha tre soluzioni reali. Se il discriminante è zero, l`equazione ha una o due soluzioni reali e alcune di queste soluzioni sono condivise. Se è negativo, l`equazione ha una sola soluzione. (Un`equazione cubica ha sempre una soluzione reale, perché il grafico è sempre almeno una volta con il X-tagli dell`asse.)
- Δ1 - 4Δ0) ÷ -27un
- (0) - 4(0)) -27(1)
- 0 - 0 27
- 0=Δ, quindi la nostra equazione ha 1 o 2 risposte.

5. calcolare C=√(√((Δ1 - 4Δ0) + Δ1)/ 2). L`ultimo valore importante da calcolare è C. Con questa importante quantità, possiamo finalmente trovare le tre soluzioni. Risolvilo come al solito, sostituendo Δ1 e Δ0 dove necessario.
- √(√((Δ1 - 4Δ0) + Δ1)/ 2)
- √(√((0 - 4(0)) + (0))/ 2)
- √(√((0 - 0) + (0))/ 2)
- 0=C

6. Calcola le tre risposte con le tue variabili. Le risposte alla tua equazione cubica sono date dalla formula (B + uC + (Δ0/uC)) / 3un, per cui voi=(-1 + √(-3))/2 e n è 1, 2 o 3. Inserisci i tuoi valori dove necessario per risolverlo: questo richiede molta matematica, ma dovrebbe darti tre possibili risposte!
Articoli sull'argomento "Risolvere un'equazione cubica"
Condividi sui social network:
Simile
Popolare