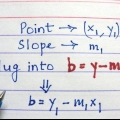La costante B è definito come `intercetta con l`asse y` Questo è il punto in cui la linea interseca l`asse y.
Entrambi X Se y sono variabili. Ad esempio, puoi specificare un valore di X risolvi, se tu y sapere, così come i valori m e B. Il X tuttavia, non è mai un solo valore: il valore cambia man mano che ci si sposta in alto o in basso nel grafico.

Ad esempio, prendiamo l`equazione y = 1/4x + 5. Dall`ultima cifra B è, lo sappiamo B è uguale a 5. Spostati verso l`alto di 5 punti sull`asse y e segna il punto. Qui è dove la tua linea retta incrocerà l`asse y.

Il primo numero (il numeratore) è il aumento da y su x. Questo è quanto si alza la linea (si sposta verticalmente).
Il secondo numero (il denominatore) è il X in y su x. Questo è quanto si sposta la linea (sposta orizzontalmente).
Ad esempio:
Una pendenza di 4/1 aumenta di 4 punti per ogni spostamento orizzontale di 1 punto. Una pendenza di -2/1 diminuisce di 2 punti per ogni spostamento orizzontale di 1 punto. Una pendenza di 1/5 aumenta di 1 punto per ogni spostamento orizzontale di 5 punti. 
Ad esempio, nel grafico sopra puoi vedere che per ogni punto che la linea aumenta, si sposta di quattro punti a destra. Questo perché la pendenza della linea è ¼ (y/x). Continui ad estendere la linea lungo entrambi i lati usando y su x. Mentre le pendenze positive aumentano, le pendenze negative diminuiscono. Una pendenza di -1/4, ad esempio, scende di un punto ogni quattro punti in cui si sposta a destra. 
Disegnare un'equazione lineare
Non so come disegnare un`equazione lineare senza una calcolatrice? Fortunatamente, rappresentare graficamente un`equazione lineare è abbastanza semplice! Hai solo bisogno di sapere alcune cose sulla tua equazione e sei pronto per partire. Iniziamo!
Passi

1. Assicurati che sia un`equazione lineare della forma y = mx + b. Questa è chiamata intercetta y ed è probabilmente il grafico più semplice di un`equazione lineare. I valori nell`equazione non devono essere numeri interi. Spesso vedi un`equazione come: y = 1/4x + 5, dove 1/4 è uguale m e 5 su B.
- La costante m si chiama `pendenza`, o `pendenza`. La collina è definito come cambiamento y rispetto al cambio di X.




2. Disegna il numero B sull`asse y. La costante B è sempre un numero razionale. qual è il numero B inoltre, trova il suo equivalente sull`asse y e disegna il suo numero in quel punto sull`asse verticale.


3. Mossa m essere in una frattura. Il numero X spesso è già una frazione, quindi non è necessario convertirla. Ma in caso contrario, convertilo semplicemente cambiando il valore di m come numeratore e 1 come denominatore.



4. Inizia ad estendere la linea da B utilizzando il noto pendio. Inizia dal valore per B: sappiamo che l`equazione supera questo punto. Estendere la linea utilizzando la pendenza per determinare i seguenti punti dell`equazione.

5. Continua ad estendere la linea (usando un righello e usando la pendenza m come una guida. Estendi la linea lungo entrambi i lati (verso l`infinito) e hai finito di rappresentare graficamente la linea. Abbastanza facile, vero??
Articoli sull'argomento "Disegnare un'equazione lineare"
Condividi sui social network:
Simile
Popolare