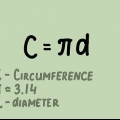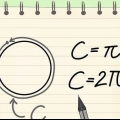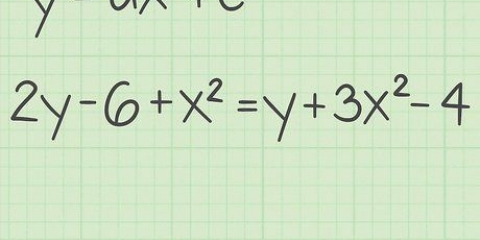Anche il pulsante π di una calcolatrice non utilizza il valore esatto di π, sebbene sia sufficientemente accurato. 
C è solo un modo più breve per scrivere "circonferenza". 
Potresti aver scritto il lato sinistro come π2r, che è anche corretto. Alla gente piace mettere i numeri prima dei simboli per rendere l`equazione più facile da leggere, ma questo non cambia il risultato dell`equazione. In un`equazione matematica, puoi sempre moltiplicare i lati sinistro e destro per la stessa quantità e ottenere comunque un`equazione corretta. 
Ad esempio, se il raggio è lungo due unità, allora 2πr = 2 x (3,14) x (2 unità) = 12,56 unità = la circonferenza. Nello stesso esempio, ma usando il pulsante π di una calcolatrice per una migliore precisione, ottieni 2 x π x 2 unità = 12,56637... unità, ma se non diversamente indicato dal tuo insegnante, puoi arrotondare il numero a 12,57 unità. 

Noi usiamo D`, non2r, perché il tuo problema di matematica ti dice cosa D si intende. Tuttavia, è importante capire questo passaggio in modo da non confonderti con il tuo insegnante o il tuo libro di matematica 2r usato dove hai a D si aspetterebbe. 
Anche il pulsante π di una calcolatrice non utilizza il valore esatto di π, sebbene sia molto preciso. 

π x d = (C / d) x d πd = C 
Ad esempio, se il diametro è sei, ottieni (3,14) x (6) = 18,84. Nello stesso esempio, ma usando il pulsante π di una calcolatrice per una maggiore precisione, ottieni π x 6 = 18,84956... ma se non diversamente indicato, puoi arrotondare il numero a 18,85. 


A = R A / π = πr / π = r √(A/π) = √(r) = r r = √(A/π) 
C = 2πr C = 2π(√(A/π)) 
La risposta per questo esempio è 13.72937... ma se non diversamente indicato, puoi arrotondare la risposta a 13.73. 


Assicurati di avvolgere il filo attorno ad esso più di una volta. Dovresti finire con un unico anello in modo che non ci sia parte del cerchio in cui la corda è avvolta doppiamente. 

Trovare la circonferenza di un cerchio
Contenuto
La circonferenza di un cerchio è la distanza attorno al suo bordo. Se un cerchio ha una circonferenza di 2 miglia, devi camminare intorno al cerchio 2 miglia prima di tornare da dove hai iniziato. Tuttavia, se stai lavorando su un problema geometrico, non devi alzarti dalla sedia. Leggi attentamente il problema per scoprire se è indicato il `raggio` (r), `diametro` (d) o `area` (A) del cerchio, quindi trova la parte di questo articolo che intende aiutarti con il compito. Ci sono anche istruzioni per trovare il perimetro di un oggetto circolare esistente che vuoi misurare.
Passi
Metodo 1 di 4: Determinazione del perimetro utilizzando il raggio

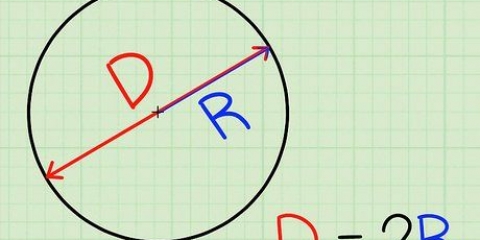
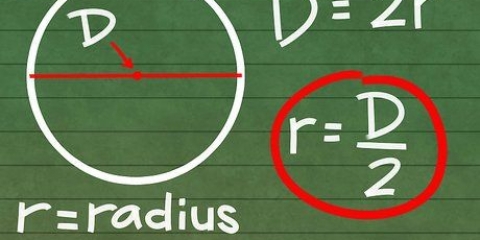
1. Disegna un "raggio" sul cerchio. Disegna una linea dal centro del cerchio a qualsiasi posizione sul bordo del cerchio. Questa linea è il "raggio" del cerchio, spesso scritto come "r" nelle equazioni e formule matematiche.
- `Nota: se il raggio non è indicato nel problema di matematica, queste potrebbero non essere le istruzioni corrette. Vedi se quelli sul diametro o sulla superficie sono più utili per il compito.

2. Disegna un "diametro" sul cerchio. Estendi la linea che hai appena disegnato in modo che raggiunga il bordo del cerchio sull`altro lato. Hai appena disegnato un secondo raggio. I due raggi aggiunti hanno una lunghezza di `2 x il raggio`, scritta come 2r. La lunghezza di questa linea è il `diametro` del cerchio, spesso scritto come D.

3. Comprendi π (`pi`). Il simbolo π, scritto anche come pi non è un numero magico che viene utilizzato in questo tipo di problemi di matematica. In realtà il numero π è stato originariamente `scoperto` misurando i cerchi: se si misura la circonferenza di un qualsiasi cerchio (ad esempio con un metro a nastro), e poi si divide per il diametro, si ottiene sempre lo stesso numero. Questo numero è insolito perché non può essere scritto come frazione semplice o decimale. Invece, possiamo arrotondarlo a un numero come 3,14, che è "abbastanza buono".

4. Scrivi la definizione di π come problema di algebra. Come spiegato sopra, π significa semplicemente `il numero che ottieni quando dividi la circonferenza per il diametro`. Sotto forma di formula matematica questo è: π = C / d. Poiché sappiamo che il diametro è uguale a 2 x il raggio, possiamo anche scriverlo come π = C / 2r.

5. Modificare questo problema in modo da risolvere questo problema per il perimetro C. Vogliamo sapere qual è il perimetro (C in questo problema di matematica). Se moltiplichi entrambi i membri per 2r ottieni π x 2r = (C / 2r) x 2r, ed è lo stesso di 2πr = C.

6. Sostituisci i numeri da risolvere con C. Ora lo sappiamo 2πr = C. Torna al problema di matematica originale per vedere cosa R (il raggio) è. Quindi sostituisci π con 3.14 o usa il pulsante π sulla calcolatrice per ottenere una risposta più precisa. Calcola 2πr con questi numeri. La risposta che ottieni è la circonferenza.
Metodo 2 di 4: Determinazione della circonferenza utilizzando il diametro

1. Capire cos`è un "diametro". Posiziona la matita sul bordo del cerchio. Disegna una linea attraverso il centro del cerchio e il bordo sull`altro lato. Questa linea (da bordo a bordo e attraverso il centro) è il `diametro` del cerchio, spesso scritto come D nei problemi di matematica.
- La linea passa per il centro esatto del cerchio, non solo in un punto qualsiasi del cerchio.
- Nota: Se l`istruzione non indica quanto è lungo il diametro, utilizzare un altro metodo.

2. Scopri cosa significa d = 2r. Il `raggio` del cerchio, scritto anche come R, è la distanza dal centro al bordo del cerchio. Poiché il diametro passa attraverso il cerchio da bordo a bordo, attraverso il centro, il diametro è uguale a due raggi. Un modo semplice per scrivere questo è d = 2r. Questo significa che tu D può sempre sostituire con 2r in un problema di matematica e viceversa.

3. Comprendi π (`pi`). Il simbolo π, scritto anche come pi non è un numero magico che viene utilizzato in questo tipo di problemi di matematica. In realtà il numero π è stato originariamente `scoperto` misurando i cerchi: se si misura la circonferenza di un qualsiasi cerchio (ad esempio con un metro a nastro), e poi si divide per il diametro, si ottiene sempre lo stesso numero. Questo numero è insolito perché non può essere scritto come frazione semplice o decimale. Invece, possiamo arrotondarlo a un numero come 3,14, che è "abbastanza buono".

4. Scrivi la definizione di π come problema di algebra. Come spiegato sopra, π significa semplicemente `il numero che ottieni quando dividi la circonferenza per il diametro`. Sotto forma di formula matematica questo è: π = circonferenza / diametro o π = C / d.

5. Modificare questo problema in modo da risolvere questo problema per il perimetro C. Vogliamo sapere qual è il perimetro, quindi dobbiamo ottenere C solo da un lato. Fallo moltiplicando ciascun lato dell`equazione per d:

6. Sostituisci i numeri e risolvi C. Torna al problema originale per vedere qual è il diametro e sostituisci la d in questa equazione con quel numero. Sostituisci π con un arrotondamento come 3,14 o usa il pulsante π sulla calcolatrice per un risultato più accurato. Moltiplica i valori e d insieme e ottieni il perimetro C.
Metodo 3 di 4: Trovare il perimetro usando l`area

1. Comprendi come viene calcolata l`area di un cerchio. Di solito la zona (un) di un cerchio non misurato direttamente. Invece, misuri il raggio (R) del cerchio, quindi calcola l`area con la formula A = R. Il motivo per cui questa formula ha senso è un po` difficile da spiegare, ma puoi saperne di più tramite questo link se sei interessato e disposto ad andare fino in fondo di un`algebra più pesante.
- Nota: Se il problema di matematica non menziona l`area del cerchio, potrebbe essere necessario utilizzare un metodo diverso da questo articolo.

2. Impara una formula per calcolare la circonferenza. La circonferenza (C) è la distanza attorno al cerchio. Generalmente lo calcoli con la formula C=2πr, ma poiché non sappiamo ancora quale sia il raggio (R), dovremo dedicare del tempo a capire il valore di R prima di poter risolvere l`equazione.

3. Usa la formula dell`area per ottenere r su un lato. Poiché A = πr, possiamo invece riorganizzare questa formula per risolvere per r. Se trovi difficili da seguire i passaggi seguenti, potresti provare prima alcuni problemi di algebra più semplici o esercitarti con alcune tecniche per comprendere l`algebra.

4. Cambia la formula del perimetro usando quello che hai trovato. Ogni volta che hai un`equazione come r = √(A/π), puoi sostituire un lato dell`equazione con l`altro?. Usiamo questa tecnica per ottenere la formula della circonferenza sopra, C=2πr, cambiare. Per questo problema non conosciamo il valore di r, ma conosciamo quello di A. Cambiamo in questo modo per rendere risolvibile il problema:

5. Sostituisci i numeri per trovare il perimetro. Usa l`area indicata nel problema per trovare il perimetro del perimetro. Ad esempio, se l`area (un) di un cerchio è di 15 unità quadrate, quindi compila 2π(√(15/π)) nella tua calcolatrice. Non dimenticare le parentesi.
Metodo 4 di 4: Determinazione della circonferenza di un cerchio reale

1. Utilizzare questo metodo per misurare oggetti circolari reali. Puoi misurare la circonferenza dei cerchi che trovi nel mondo reale, non solo nei problemi. Provalo su una ruota di bicicletta, una pizza o una moneta.

2. Prendi un pezzo di spago e un righello. La corda dovrebbe essere abbastanza lunga da avvolgere il cerchio una volta e abbastanza flessibile da adattarsi perfettamente. Avrai bisogno di qualcosa per misurare la corda in seguito, come un righello o un metro a nastro. La corda sarà più facile da misurare se il righello è più lungo della lunghezza della corda.

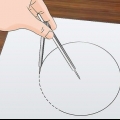
3. Avvolgi lo spago una volta attorno al cerchio. Inizia posizionando un`estremità della corda lungo il bordo del cerchio. Avvolgi la corda attorno al cerchio e tirala stretta. Se misuri una moneta o un altro oggetto sottile, potresti non essere in grado di stringere il filo attorno ad esso. Appoggia l`oggetto circolare in piano e disponi il filo attorno ad esso, il più stretto possibile.

4. Segna o taglia la corda. Trova il punto sulla corda in cui termina l`anello e tocca l`estremità della corda con cui hai iniziato. Segna questo posto con un pennarello o taglia la corda in questo punto.

5. Allenta la corda e misurala con un righello. Prendi la corda avvolta e misurala con un righello. Se hai usato un pennarello, misura solo dall`estremità della corda al pennarello. Questa è la parte della stringa che avvolge il cerchio e poiché la circonferenza di un cerchio è solo la distanza attorno al cerchio, hai trovato la risposta! La lunghezza di questa corda è uguale alla circonferenza del cerchio.
Consigli
- Puoi scrivere il plurale di raggio come raggi o come raggi.
Articoli sull'argomento "Trovare la circonferenza di un cerchio"
Condividi sui social network:
Simile
Popolare