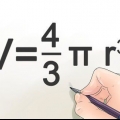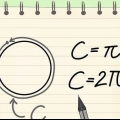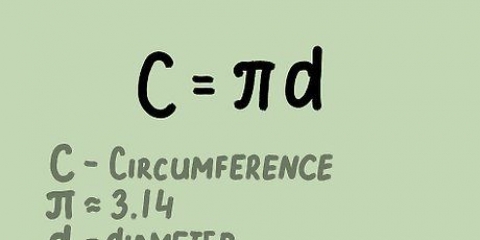Come Calcolare il Raggio di una Sfera

Contenuto

Passi
Consigli

Il raggio di una sfera (abbreviato come variabile R o R) è la distanza dal centro esatto della sfera a un punto sulla superficie di quella sfera. Proprio come cerchi, il raggio di una sfera è spesso un primo dato fondamentale per il calcolo del diametro, della circonferenza, dell`area e del volume di una sfera. Tuttavia, puoi anche lavorare all`indietro dal diametro, dalla circonferenza, ecc. per trovare il raggio della sfera. Usa la formula appropriata per i dati che hai.

Passi

Metodo 1 di 3: utilizzo delle formule del raggio

Immagine titolata Trova il raggio di una sfera Step 1

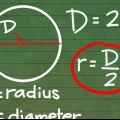
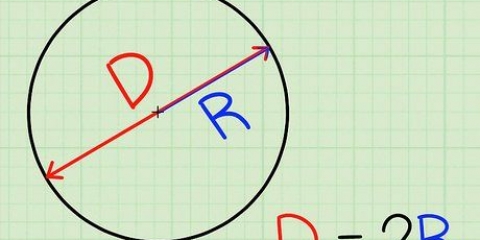
1. Determina il raggio se conosci il diametro. Il raggio è mezzo diametro, quindi usi la formula r = D/2. Questo è identico al metodo per calcolare il raggio di un cerchio dato il diametro.

Se hai una sfera con un diametro di 16 cm, calcola il raggio con 16/2 = 8 cm. Se il diametro è 42, allora il raggio 21.

Immagine titolata Trova il raggio di una sfera Step 2

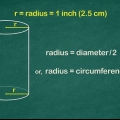
2. Determina il raggio se conosci la circonferenza. Usa la formula C/2π. Poiché la circonferenza è uguale a πD, che a sua volta è uguale a 2πr, si calcola il raggio dividendo la circonferenza per 2π.

Se hai una sfera con una circonferenza di 20 m, troverai il raggio con 20/2π = 3.183 m.

La stessa formula può essere utilizzata per convertire tra il raggio e la circonferenza di un cerchio.

Immagine titolata Trova il raggio di una sfera Step 3

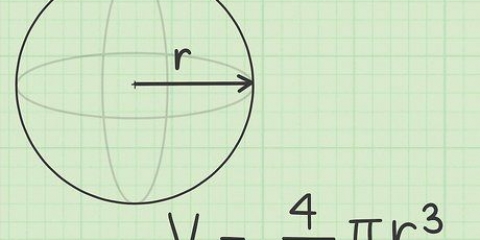
3. Calcola il raggio se conosci il volume della sfera. Usa la formula ((V/π)(3/4)). Il volume di una sfera si ricava dall`equazione V = (4/3)πr.Risolvendo l`equazione per r, si ottiene ((V/π)(3/4)) = r, quindi diventa chiaro che il raggio di una sfera è uguale al volume diviso per π, moltiplicato per 3/4 , al 1/3 di potenza (o radice cubica).

Se hai una sfera con un volume di 100 cm, ottieni il raggio come segue:

((V/π)(3/4)) = r

((100/π)(3/4)) = r

((31.83)(3/4)) = r

(23.87) = R

2.88 = R

Immagine titolata Trova il raggio di una sfera Step 4

4. Determina il raggio della superficie. Usa la formula r = √(A/(4π)). L`area di una sfera viene calcolata utilizzando l`equazione A = 4πr. Risolvendo l`equazione per r si ottiene √(A/(4π)) = r, il che significa che il raggio di una sfera è uguale alla radice quadrata della sua area divisa per 4π. Puoi anche alimentare (A/(4π)) a 1/2 per lo stesso risultato.

Se hai una sfera con un`area di 1200 cm, calcoli il raggio come segue:

√(A/(4π)) = r

√(1200/(4π)) = r

√(300/(π)) = r

√(95.49) = r

9,77 cm = R

Metodo 2 di 3: definizione dei termini chiave

Immagine titolata Trova il raggio di una sfera Step 5

1. Conoscere le dimensioni di base di una sfera. Il raggio (R) è la distanza dal centro esatto della sfera a qualsiasi punto sulla superficie della sfera. In generale, puoi trovare il raggio di una sfera se ne conosci il diametro, la circonferenza, il volume o l`area.

Diametro (D): la lunghezza della linea che passa per il centro di una sfera & ndash; raddoppiare il raggio. Il diametro è la lunghezza di una linea passante per il centro della sfera: da un punto all`esterno della sfera a un punto corrispondente direttamente opposto ad essa. In altre parole, la massima distanza possibile tra due punti della sfera.
Circonferenza (C): la distanza unidimensionale attorno alla sfera nel suo punto più largo. In altre parole, il perimetro della sezione circolare di una sfera il cui piano passa per il centro della sfera.
Volume (V): lo spazio tridimensionale all`interno della sfera. È il "spazio occupato dalla sfera".
Zona (A): lo spazio bidimensionale sulla superficie esterna della sfera. La quantità di spazio piatto che copre l`esterno della sfera.
pi (π): una costante che esprime il rapporto tra la circonferenza del cerchio e il diametro del cerchio. Le prime 10 cifre di Pi sono sempre 3.141592653, sebbene questo sia solitamente arrotondato a 3.14.

Immagine titolata Trova il raggio di una sfera Step 6

2. Utilizzare letture diverse per determinare il raggio. È possibile utilizzare il diametro, il perimetro, il volume e l`area per calcolare il raggio di una sfera. Se conosci la lunghezza del raggio, puoi calcolare uno qualsiasi di questi numeri. Quindi, per trovare il raggio puoi invertire le formule per calcolare queste parti. Impara le formule che coinvolgono il raggio per calcolare diametro, circonferenza, area e volume.

D = 2r. Proprio come cerchi è il diametro di una sfera doppio del suo raggio.

C = πD o 2πr. Proprio come cerchi è la circonferenza di una sfera uguale a π volte il diametro. Poiché il diametro è doppio del raggio, possiamo anche dire che la circonferenza è uguale al doppio del raggio moltiplicato per π.

V = (4/3)πr. Il volume di una sfera è il suo raggio rispetto al cubo (r x r x r), per π, per 4/3.

A = 4πr. L`area di una sfera è il suo raggio alla seconda potenza (r x r), volte π, volte 4. Poiché la circonferenza di un cerchio è uguale a πr, si può anche dire che l`area di una sfera è pari a quattro volte l`area di un cerchio, in quanto formata dalla sua circonferenza.

Metodo 3 di 3: Trovare il raggio come distanza tra due punti

Immagine titolata Trova il raggio di una sfera Step 7

1. Determina le coordinate (x, y, z) del centro della sfera. Un modo per pensare al raggio di una sfera è come la distanza tra il centro della sfera e qualsiasi punto sulla sua superficie. Poiché questo è vero, puoi determinare il raggio della sfera utilizzando le coordinate del centro e un punto sulla superficie della sfera, calcolando la distanza tra i due punti utilizzando una variante della formula della distanza standard. Per iniziare, trova le coordinate del centro della sfera. Nota che una sfera è tridimensionale, questo sarà un punto (x, y, z) invece di un punto (x, y).

Questo è più facile da capire con un esempio. Supponiamo che sia data una sfera con centro(-1, 4, 12). Nei prossimi passi useremo questo punto per determinare il raggio.

Immagine titolata Trova il raggio di una sfera Step 8

2. Determina le coordinate di un punto sulla superficie della sfera. Quindi è necessario determinare le coordinate (x, y, z) di un punto sulla superficie della sfera. Questo è possibile ogni punto sulla superficie della sfera. Poiché per definizione tutti i punti sulla superficie di una sfera sono equidistanti dal centro, puoi usare qualsiasi punto per determinare il raggio.

Nel contesto del nostro esempio di assegnazione, affermiamo che il punto (3, 3, 0) sulla superficie della sfera, è dato. Calcolando la distanza tra questo punto e il centro, possiamo trovare il raggio.

Immagine titolata Trova il raggio di una sfera Step 9

3. Determina il raggio con la formula d = √((x₂ - X₁) + (s₂ - y₁) + (z₂ - z₁)). Ora che conosci il centro della sfera e un punto sulla superficie della sfera, puoi scoprire il raggio calcolando la distanza tra di loro. Usa la formula della distanza tridimensionale d = √((x₂ - X₁) + (s₂ - y₁) + (z₂ - z₁)), dove d è la distanza, (x₁,y₁,z₁) rappresenta le coordinate del punto centrale, e(x₂,y₂,z₂) sta per le coordinate del punto sulla superficie, per determinare la distanza tra entrambi i punti.

Nel nostro esempio sostituiamo (4, -1, 12) con (x₁,y₁,z₁) e (3, 3, 0) per (x₂,y₂,z₂), dove risolviamo come segue:

d = √((x₂ - X₁) + (s₂ - y₁) + (z₂ - z₁))

d = √((3 - 4) + (3 - -1) + (0 - 12))

d = √((-1) + (4) + (-12))

d = √(1 + 16 + 144)

d = √(161)

d = 12,69. Questo è il raggio della nostra sfera.

Immagine titolata Trova il raggio di una sfera Step 10

4. Sappi che in generale, r = √((x₂ - X₁) + (s₂ - y₁) + (z₂ - z₁)). In una sfera, ogni punto della superficie è alla stessa distanza dal centro della sfera. Prendiamo la formula della distanza tridimensionale sopra e sostituiamo la variabile "D" dalla variabile "R" del raggio, allora otteniamo un`equazione che ci permette di trovare il raggio in un dato centro (x₁,y₁,z₁) e qualsiasi punto corrispondente sulla superficie (x₂,y₂,z₂).

Al quadrato di entrambi i membri di questa equazione otteniamo: r = (x₂ - X₁) + (s₂ - y₁) + (z₂ - z₁). Nota: Questo è essenzialmente equivalente all`equazione standard per una sfera (r = x + y + z), assumendo che il suo centro sia uguale a (0,0,0).

Consigli

L`ordine delle operazioni è importante. Se non sei sicuro di come funzionano le regole matematiche e la tua calcolatrice supporta le parentesi, assicurati di usarle.
Questo articolo è stato creato perché questo argomento era molto richiesto. Tuttavia, se stai cercando di capire la geometria spaziale per la prima volta, probabilmente è meglio iniziare dall`altro lato: calcolare le proprietà di una sfera quando è dato il suo raggio.
Pi o π è una lettera greca che indica il rapporto tra il diametro di un cerchio e la sua circonferenza. È un numero irrazionale e non può essere scritto come rapporto di numeri reali. Ci sono molte approssimazioni e 333/106 dà pi greco a quattro cifre decimali. Oggi la maggior parte delle persone ricorda l`approssimazione 3.14 che di solito è abbastanza accurata per gli scopi quotidiani.