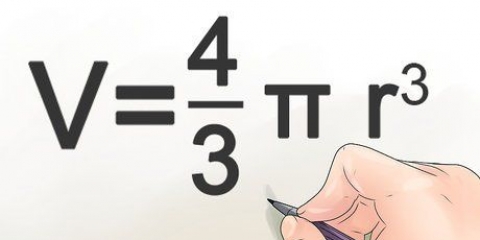Calcolo della Massa di una Sfera: 13 Passaggi (con Immagini)

Contenuto

Passi
Consigli

In poche parole, una sfera è una palla rotonda solida. Per calcolare la massa di una sfera, è necessario conoscere la dimensione (volume) della sfera e la sua densità. Puoi calcolare il volume usando il raggio, la circonferenza o il diametro della sfera. Puoi anche immergere la sfera nell`acqua per trovare il volume in base allo spostamento dell`acqua. Se conosci il volume, puoi moltiplicarlo per la densità per trovare la massa.

Passi

Parte 1 di 3: Determinazione del volume di una sfera

Immagine titolata Calcola la massa di una sfera Step 1

1. Usa la formula per il volume di una sfera. Una sfera è un solido circolare in tre dimensioni. La formula principale per il volume di una sfera è:

$Volume = \frac{4}{3} π R^{3}$ ${displaystyle {text{Volume}}={frac {4}{3}}pi r^{3}}$

$π = 3, 14$ ${ displaystyle pi = 3,14}$
$R = raggio$ ${displaystyle r={text{raggio}}}$

Immagine titolata Calcola la massa di una sfera Step 2

2. Trova il volume di una sfera se ne conosci il raggio. Il raggio di una sfera è la misura dal centro della sfera al bordo esterno. Se ti viene assegnato un problema per calcolare il volume, probabilmente viene fornito il raggio. In caso contrario, il raggio può essere difficile da misurare perché non è possibile determinare con precisione il centro di un oggetto solido.

Supponiamo che ti venga detto che esiste una sfera con un raggio di 10 cm. Trova il volume come segue:

Volume = \frac{4}{3} π R^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi r^{3}}$

Volume = \frac{4}{3} * (3, 14) * 10^{3}

${displaystyle {text{Volume}}={frac {4}{3}}*(3.14)*10^{3}}$

Volume = 4, 18667 * 1000

${displaystyle {text{Volume}}=4,18667*1000}$

Volume = 4186, 67 {centimetro}^{3}

${displaystyle {text{Volume}}=4186,67{text{cm}}^{3}}$

Immagine titolata Calcola la massa di una sfera Step 3

3. Determinare il volume se il diametro è specificato. Un`altra possibilità è che per una certa situazione venga dato il diametro di una sfera. Il diametro è uguale al doppio del raggio. In effetti, il diametro è la distanza da un bordo della sfera attraverso il centro all`altro bordo. Per calcolare il volume dal diametro (d), rivedere la formula come segue:

Volume = \frac{4}{3} π (\frac{D}{2})^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi ({frac {d}{2}})^{3}}$

Come esempio di questo calcolo, determinare il volume di una sfera con un diametro di 10 cm.

Volume = \frac{4}{3} π (\frac{D}{2})^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi ({frac {d}{2}})^{3}}$

Volume = \frac{4}{3} π (\frac{10}{2})^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi ({frac {10}{2}})^{3}}$

Volume = \frac{4}{3} * (3, 14) * (5^{3})

${displaystyle {text{Volume}}={frac {4}{3}}*(3.14)*(5^{3})}$

Volume = 4, 18667 * 125

${displaystyle {text{Volume}}=4,18667*125}$

Volume = 523, 3 {centimetro}^{3}

${displaystyle {text{Volume}}=523,3{text{cm}}^{3}}$

Immagine titolata Calcola la massa di una sfera Step 4

4. Rivedi la formula se conosci il perimetro. La circonferenza di una sfera è probabilmente la più facile da misurare direttamente. Puoi usare un metro a nastro, avvolgerlo delicatamente intorno alla parte più larga del bulbo e prendere la misura. Forse la circonferenza è data in una dichiarazione. Per trovare il volume che inizia con il perimetro (C), rivedere la formula come segue:

Volume = \frac{4}{3} π R^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi r^{3}}$

Volume = \frac{4}{3} π * (C 2 π)^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi *({frac {C}{2pi }})^{3}}$

Volume = \frac{4}{3} π * (C 3 8 π 3)

${displaystyle {text{Volume}}={frac {4}{3}}pi *({frac {C^{3}}{8pi ^{3}}})}$

Volume = C 3 6 π 2

${displaystyle {text{Volume}}={frac {C^{3}}{6pi ^{2}}}}$

Immagine titolata Calcola la massa di una sfera Step 5

5. Calcola il volume se conosci il perimetro. Supponiamo di ottenere una sfera e di misurare la circonferenza a 32 cm. Trova il volume come segue:

Volume = C 3 6 π 2

${displaystyle {text{Volume}}={frac {C^{3}}{6pi ^{2}}}}$

Volume = 323 6 * 3, 14 2

${displaystyle {text{Volume}}={frac {32^{3}}{6*3.14^{2}}}}$

Volume = 32.768 59, 158

${displaystyle {text{Volume}}={frac {32,768}{59,158}}}$

Volume = 553, 9 {centimetro}^{3}

${displaystyle {text{Volume}}=553,9{text{cm}}^{3}}$

Immagine titolata Calcola la massa di una sfera Step 6

6. Misurare il volume in base allo spostamento d`acqua. Un ultimo metodo pratico per misurare il volume consiste nell`immergere il bulbo nell`acqua. Devi avere un bicchiere abbastanza grande da sommergere il bulbo con segni di volume precisi.

Versare abbastanza acqua nella tazza per coprire il bulbo. Nota il volume.

Versa il bulbo nell`acqua. Si noti che il livello dell`acqua è in aumento. Nota il nuovo volume.

Sottrarre il primo volume dal secondo. Il risultato è il volume della sfera.

Supponiamo che il livello dell`acqua salga da 100 ml a 625 ml quando si immerge il bulbo. Quindi il volume è di 525 ml. Si noti che 1 ml=1 cm.

Parte 2 di 3: Calcolo della massa dal volume

Immagine titolata Calcola la massa di una sfera Step 7

1. Determina la densità. Per calcolare la massa dal volume, è necessario conoscere la densità dell`oggetto. Materiali diversi hanno densità diverse. Ad esempio, considera una sfera di polistirolo e confronta il suo peso con una sfera di ferro della stessa dimensione. Il ferro ha una densità molto maggiore e avrà quindi una massa maggiore.

Puoi cercare le densità di molti materiali solidi online, nei libri di testo o in un Binas.
Ad esempio, ecco le densità registrate di alcuni materiali solidi:

Alluminio = 2700 kg/mq
Burro = 870 kg/mq
Piombo = 11.350 kg/mq
Legno pressato = 190 kg/m

Immagine titolata Calcola la massa di una sfera Step 8

2. Converti le unità secondo necessità. Le unità utilizzate per calcolare il volume devono corrispondere alle unità di volume nella densità misurata. In caso contrario, devi convertirli.

Tutti gli esempi nella sezione precedente hanno prodotto volumi misurati in centimetri cubi. Tuttavia, la tabella della densità indicata fornisce densità basate su metri cubi. Perché ci sono 100 centimetri in un metro, ci sono 10 centimetri cubi in un metro cubo. Dividi le densità date per 10 per ottenere la densità in unità di kg/cm (facile facilmente spostando la virgola decimale di sei spazi a sinistra).

Per i quattro materiali precedentemente elencati, le densità convertite sono le seguenti:

Alluminio = 2700 kg/m = 0,0027 kg/cm

Burro = 870 kg/m3 = 0,00087 kg/cm

Piombo = 11.350 kg/mq = 0,01135 kg/cm

Legno pressato = 190 kg/m = 0,00019 kg/cm

Immagine titolata Calcola la massa di una sfera Step 9

3. Moltiplica il volume per la densità per trovare la massa. La formula per la densità è

Densità = \frac{Massa}{Volume}

${displaystyle {text{Densità}}={frac {text{Massa}}{text{Volume}}}}$ , come forse ricorderai. Se lo riorganizzi per trovare la massa, l`equazione diventa

Densità * Volume = Massa

${displaystyle {text{Densità}}*{text{Volume}}={text{Massa}}}$ .

Utilizzando i quattro materiali precedentemente citati, alluminio, burro, piombo e legno pressato, si determina la massa di una sfera con un volume di 500 cm.

Alluminio : 500 {centimetro}^{3} * 0, 0027 \frac{kg}{} centimetro 3 = 1, 35 kg

${displaystyle {text{alluminio}}:500{text{ cm}}^{3}*0,0027{frac {text{kg}}{{text{cm}}^{3}} }= 1,35{testo{ kg}}}$

Burro : 500 {centimetro}^{3} * 0, 00087 \frac{kg}{} centimetro 3 = 0, 435 kg

${displaystyle {text{burro}}:500{text{ cm}}^{3}*0,00087{frac {text{kg}}{{text{cm}}^{3}} }= 0,435{testo{ kg}}}$

Guida : 500 {centimetro}^{3} * 0, 01135 \frac{kg}{} centimetro 3 = 5, 675 kg

${displaystyle {text{Lead}}:500{text{ cm}}^{3}*0,01135{frac {text{kg}}{{text{cm}}^{3}} }= 5.675{text{ kg}}}$

Legno pressato : 500 {centimetro}^{3} * 0, 00019 \frac{kg}{} centimetro 3 = 0, 095 kg

${displaystyle {text{Legno pressato}}:500{text{ cm}}^{3}*0,00019{frac {text{kg}}{{text{cm}}^{3} }} =0,095{testo{ kg}}}$

Parte 3 di 3: Risoluzione di un problema di esempio

Immagine titolata Calcola la massa di una sfera Step 10

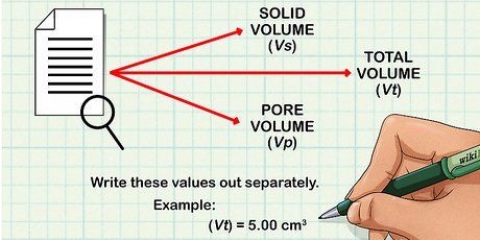
1. Leggi attentamente il compito. Quando si risponde ai problemi con i calcoli di massa, leggere attentamente l`intera dichiarazione. Durante la lettura, può essere utile evidenziare la voce. Leggi attentamente l`intero problema per vedere cosa ti verrà chiesto di risolvere. Si consideri ad esempio il seguente problema:

Una grande sfera di ottone massiccio ha un diametro di 1,2 m. Determina la massa della sfera.

Immagine titolata Calcola la massa di una sfera Step 11

2. Organizza i dati noti e sconosciuti. Se leggi attentamente la dichiarazione, puoi determinare che il diametro è dato, quindi usa la formula modificata:

Volume = \frac{4}{3} π (\frac{D}{2})^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi ({frac {d}{2}})^{3}}$

Hai anche letto che la sfera è di ottone. Devi cercare la densità dell`ottone nel tuo Binas o da un`altra fonte.

Sul sito, EngineeringToolbox.com, puoi cercare che la densità dell`ottone è 8480 kg/m. Poiché il diametro della sfera è espresso in metri, il suo volume è calcolato in metri cubi, quindi non è necessario convertire la densità.

Immagine titolata Calcola la massa di una sfera Step 12

3. Calcola il volume. Per calcolare il volume, inserisci la formula appropriata, inserisci i dati che conosci ed esegui i calcoli come segue:

Volume = \frac{4}{3} π (\frac{D}{2})^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi ({frac {d}{2}})^{3}}$

Volume = \frac{4}{3} π (1, 2 2)^{3}

${displaystyle {text{Volume}}={frac {4}{3}}pi ({frac {1,2}{2}})^{3}}$

Volume = 4, 18667 * 0, 6^{3}

${displaystyle {text{Volume}}=4,18667*0,6^{3}}$

Volume = 4, 18667 * 0, 216

${displaystyle {text{Volume}}=4,18667*0,216}$

Volume = 0, 90432 m^{3}

${displaystyle {text{Volume}}=0,90432{text{ m}}^{3}}$

Immagine titolata Calcola la massa di una sfera Step 13

4. Usa la densità per calcolare la massa. Pensalo

Massa = Densità * Volume

${displaystyle {text{Massa}}={text{Densità}}*{text{Volume}}}$ . Inserisci i valori che conosci nella formula per trovare la massa:

Massa = Densità * Volume

${displaystyle {text{Massa}}={text{Densità}}*{text{Volume}}}$

Massa = 8480 \frac{kg}{} m 3 * 0, 90432 m^{3}

${displaystyle {text{Mass}}=8480{frac {text{ kg}}{{text{ m}}^{3}}}*0,90432{text{ m}}^{3 }}$

Massa = 7668, 6 kg

${displaystyle {text{Massa}}=7668,6{testo{ kg}}}$

Consigli

Questa spiegazione presuppone che la densità della sfera sia la stessa ovunque. Questo è presupposto nella maggior parte dei problemi matematici e fisici. Tuttavia, è possibile che il nucleo di una sfera sia fatto di materiale diverso dalla superficie.

Articoli sull'argomento "Calcola la massa di una sfera"

Calcola la massa

Calcola la percentuale di massa

Calcola volume e densità

Calcolo del raggio di una sfera

Condividi sui social network: