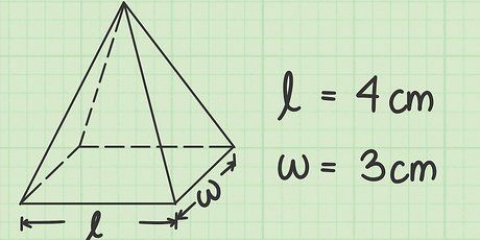Per trovare s³, moltiplica s tre volte per se stesso: s³ = s x s x s 
Se non sei sicuro al 100% che la tua forma sia un cubo, misura tutti i lati per vedere se sono uguali. In caso contrario, dovrai utilizzare il metodo seguente per calcolare il volume di una trave. Nota: nelle immagini di esempio le misure sono espresse in pollici (in), tuttavia utilizziamo centimetri (cm). 




Esempio: la lunghezza di questa trave è di 4 cm, quindi l = 4 cm. Non preoccuparti troppo di quale lato è la lunghezza, ecc. Finché misuri solo tre lati diversi, il risultato sarà lo stesso. 
Esempio: la larghezza di questa trave è 3 cm, quindi b = 3 cm. Se misuri la trave con un righello o un metro a nastro, non dimenticare di annotare tutto nella stessa unità di misura. 
Esempio: l`altezza di questa barra è 6 cm, quindi h = 6 cm. 
In questo esempio, l = 4, b = 3 e h = 6. Pertanto, il risultato è V = 4 x 3 x 6 = 72. 
Ad esempio, se le dimensioni della trave fossero in metri, otterresti l = 2 m, w = 4 m e h = 8 m. Il volume sarebbe quindi 2 m x 4 m x 8 m = 64 m³. 

Nella maggior parte dei casi è sufficiente arrotondare pi a 3,14. Chiedi al tuo insegnante cosa vuole. La formula per trovare il volume di un cilindro è in realtà molto simile a quella del volume di una trave: si moltiplica l`altezza della sagoma per l`area della base. Per una trave, l`area della base è l x b, per un cilindro è π x r², l`area di una circonferenza di raggio r. 

Un`altra opzione è misurare la circonferenza del cerchio (la distanza attorno ad esso) con un pezzo di spago o un metro a nastro. Quindi inserisci il risultato in questa formula: C (circonferenza) è 2 x π x r. Dividi la circonferenza per 2 x π (6.28) e hai il raggio. Ad esempio, se la circonferenza che hai misurato è 8 cm, il raggio è 1,27 cm. Se hai davvero bisogno di una misurazione esatta, puoi utilizzare entrambi i metodi per vedere se i risultati sono gli stessi. In caso contrario, ricontrolla. Il metodo della circonferenza di solito fornisce un risultato più accurato. 
Se il raggio è 4 cm, l`area del cerchio è A = π x 4². 4² = 4 x 4 o 16. 16 xπ = 16 x 3,14 = 50,24 cm². Se si conosce il diametro della base, anziché il raggio, ricordarsi che d = 2 x r. Quindi devi dividere il diametro per due per trovare il raggio. 

V = π x 4² x 10 π x 4²= 50,24 50,24 x 10 = 502,4 V = 502,4 


La formula per le piramidi diritte, dove l`apice è direttamente sopra il centro della base, è la stessa delle piramidi inclinate, dove l`apice non è al centro. 
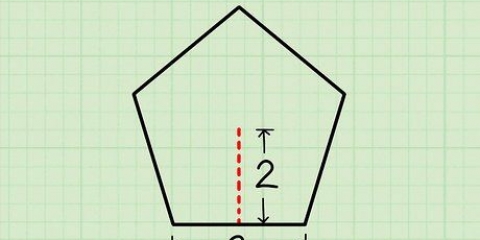
La formula per l`area di un triangolo è A = 1/2 x b x h, dove b è la base e h è l`altezza. È possibile calcolare l`area di un qualsiasi poligono regolare con la formula A = 1/2 xpxa, dove A è l`area, p è il perimetro e a è l`apotema, che è la distanza dal centro della forma a il centro di uno dei lati. Puoi anche semplificarti la vita e utilizzare un normale calcolatore di poligoni online. 

Se avessimo avuto un`altra piramide con base di area 26 e altezza 8, il risultato sarebbe stato: 1/3 x 26 x 8 = 69,33. 


La parte π x r² si riferisce all`area del cerchio che forma la base del cono. Quindi la formula per il volume del cono è 1/3 x l x h, proprio come la formula per la piramide nel metodo sopra! 
In questo esempio il raggio è di 3 cm. Se lo mettiamo nella formula otteniamo: A = π x 3². 3² = 3 x3, o 9, quindi A = π x 9. A = 28,27 cm². 


Nel nostro esempio che è 141,35 x 1/3 = 47,12, il volume del cono. Di nuovo: 1/3 x π x 3² x 5 = 47,12. 




Ad esempio, se misuri la pallina e vedi che la circonferenza è 18 cm, dividila per 6,28, sai che il raggio è 2,87 cm. Può essere complicato misurare una sfera, quindi è meglio misurarla tre volte e fare la media (aggiungi le tre misurazioni insieme e dividi per tre) per ottenere la misurazione il più accurata possibile. Ad esempio, se hai misurato tre volte e i risultati sono stati 18 cm, 17,75 cm e 18,2 cm, aggiungilo insieme (18 + 17,5 + 18,2 = 53,95) e dividi per 3 (53,95/3 = 17,98). Utilizzi questa media per calcolare il volume. 


Quindi nel nostro esempio diventa 36 x 3,14 = 113,09. 
Calcola volume
Contenuto
Il volume di una figura è lo spazio tridimensionale che la figura occupa. Puoi rappresentare il volume come la quantità di acqua (o aria, sabbia, ecc.).) che si adatterebbe allo stampo se fosse completamente pieno. Le unità di misura del volume comunemente utilizzate sono i centimetri cubi e i metri cubi.Questo articolo ti insegnerà come calcolare il volume di sei diverse forme tridimensionali che si incontrano comunemente nei test di matematica, inclusi il cubo, la sfera e il cono. Vedrai che ci sono molte somiglianze che ti renderanno facile ricordare. Vedi se riesci a trovare quelle corrispondenze!
Passi
Metodo 1 di 6:Calcolo del volume di un cubo

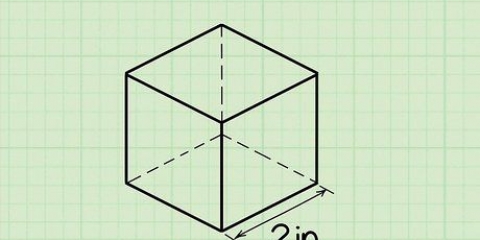
1. Riconosci un cubo. Un cubo è una forma tridimensionale con sei facce quadrate identiche.In altre parole, è una scatola con lati uguali ovunque.
- Un dado è un buon esempio di cubo che potresti avere a casa. Anche i cubetti di zucchero o i blocchi per bambini sono spesso cubetti.

2. Impara la formula per calcolare il volume del cubo. Poiché tutte le lunghezze dei lati del cubo sono della stessa lunghezza, la formula per calcolare il volume del cubo è molto semplice. Il luogo in cui due lati si incontrano è chiamato costola. Abbreviamo il volume a "V". Le nervature, o la lunghezza del lato, le chiamiamo qui "S". La formula diventa quindi V = s³

3. Trova la lunghezza di un lato del cubo. A seconda del compito, queste informazioni potrebbero essere già presenti, ma potresti anche doverle misurare tu stesso con un righello. Ricorda, poiché è un cubo, tutte le lunghezze dei lati dovrebbero essere uguali, quindi non importa quale misuri.

4. Metti la lunghezza del lato nella formula V = s³ e calcolala. Ad esempio, se hai misurato che la lunghezza del lato del tuo cubo è 5 cm, dovresti scrivere la formula come segue: V = (5)³. 5 x 5 x 5 = 125 cm³, quindi questo è il volume del tuo cubo!

5. Assicurati di scrivere la tua risposta in centimetri cubi. Nell`esempio sopra, il cubo è stato misurato in centimetri, quindi la risposta deve essere data in centimetri cubi. Se la lunghezza del lato del cubo fosse stata di 3 metri, il volume sarebbe stato V = (3 m)³ = 27 m³.
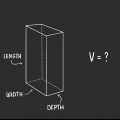
Metodo 2 di 6:Calcolo del volume di una trave.

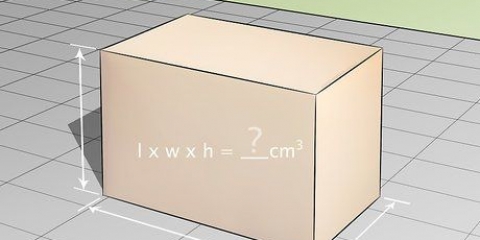
1. Riconosci un raggio. Una trave è una figura composta da sei superfici rettangolari. Quindi è in realtà un rettangolo tridimensionale, una specie di scatola.
- In realtà, un cubo è solo una trave speciale, in cui tutti i lati sono uguali.

2. Impara la formula per calcolare il volume di una trave. La formula per il volume di una trave è V = lunghezza (l) x larghezza (w) x altezza (h) o V = l x l x h. Nota: le immagini che accompagnano questi esempi mostrano "w" per larghezza.

3. Trova la lunghezza del raggio. La lunghezza è il lato più lungo della trave che è parallelo al suolo o alla superficie su cui poggia. La lunghezza potrebbe essere già indicata sull`immagine, oppure potrebbe essere necessario misurarla con un righello.

4. Trova la larghezza del raggio. La larghezza della trave può essere trovata misurando il lato corto che è parallelo al suolo o alla superficie su cui poggia. Ancora una volta, prima controlla se è già indicato sull`immagine e misuralo altrimenti con il tuo righello.

5. Trova l`altezza del raggio. L`altezza è la distanza dal suolo o dalla superficie su cui poggia la trave alla sommità della trave. Controlla se è già indicato nell`immagine e misuralo in modo diverso con il tuo righello o metro.

6. Inserisci le dimensioni nella formula e calcolala. Ricorda che V = l x l x h.

7. Assicurati di scrivere la tua risposta in centimetri cubi. Il risultato è quindi 72 centimetri cubi, ovvero 72 cm³.
Metodo 3 di 6: Calcolo del volume di un cilindro

1. Scopri come identificare un cilindro. Un cilindro è una forma tridimensionale con due estremità rotonde identiche collegate da un unico lato curvo. In realtà è un`asta dritta e rotonda.
- Una lattina è un buon esempio di cilindro o batteria AA.

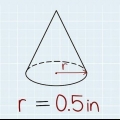
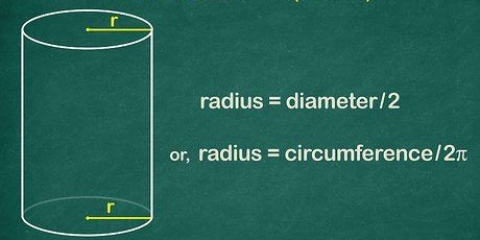
2. Memorizza la formula per il volume di un cilindro. Per calcolare il volume di un cilindro, devi conoscerne l`altezza e il raggio della sua base circolare.Il raggio è la distanza dal centro del cerchio al bordo. La formula è V =π x r² x h, dove V è il volume, r è il raggio, h è l`altezza e π è la costante pi.

3. Trova il raggio della base. Se è già indicato nell`immagine, basta compilarlo. Se hai il diametro invece del raggio, dividilo per 2 per trovare il raggio (d = 2 x r).

4. Misurare la forma se il raggio non è specificato. Nota che può essere difficile misurare il raggio esatto di un cerchio. Un`opzione è misurare il cerchio nel suo punto più largo con il righello dall`alto verso il basso, dividendolo per due.

5. Calcola l`area del cerchio alla base. Metti il raggio nella formula π x r². Moltiplica il raggio per se stesso e moltiplica il risultato per π. Ad esempio:

6. Trova l`altezza del cilindro. Questa è semplicemente la distanza tra le due basi circolari, ovvero la distanza dalla superficie su cui poggia il cilindro alla sommità del cilindro. Verifica se la lunghezza è già indicata nell`immagine o misurala in modo diverso con il tuo righello o metro a nastro.

7. Moltiplica l`area della base per l`altezza del cilindro per trovare il volume. Metti i valori nella formula V =π x r² x h. Nel nostro esempio con un raggio di 4 cm e un`altezza di 10 cm:

8. Ricordati di scrivere la tua risposta in centimetri cubi. In questo esempio il cilindro è stato misurato in centimetri, quindi la risposta deve essere scritta in centimetri cubi: V = 502,4cm³. Se il cilindro fosse misurato in metri, il volume dovrebbe essere scritto in metri quadrati (m³).
Metodo 4 di 6: Calcolo del volume di una piramide regolare

1. Scopri cos`è una piramide regolare. Una piramide è una forma tridimensionale con un poligono alla base e lati che si assottigliano verso l`alto (la punta della piramide).Una piramide regolare è una piramide la cui base è un poligono regolare, il che significa che tutti i lati e gli angoli di questo poligono sono uguali.
- Di solito una piramide è raffigurata con una base quadrata e lati che si assottigliano in un punto, ma la base di una piramide può effettivamente avere 5, 6 o 100 lati!
- Una piramide con un cerchio come base è chiamata cono, di cui parleremo nel prossimo metodo.

2. Impara la formula per calcolare il volume della piramide regolare. La formula per il volume di una piramide regolare è V = 1/3 x b x h, dove b è l`area della base e h è l`altezza della piramide, ovvero la distanza verticale dalla base alla sommità.

3. Calcola l`area della base. La formula per questo dipende dal numero di lati della base. Nel nostro esempio la base è un quadrato con i lati di 6 cm. Ricorda che la formula per calcolare l`area di un quadrato è A = s². Quindi con la nostra piramide che è 6 x 6 = 36 cm².

4. Trova l`altezza della piramide. Nella maggior parte dei casi sarà indicato sull`immagine. Nel nostro esempio, l`altezza della piramide è di 10 cm.

5. Moltiplica l`area della base della piramide per l`altezza e dividi per 3 per trovare il volume. Ricorda che la formula è V = 1/3 x b x h. Nel nostro esempio la piramide ha una base con un`area di 36 e un`altezza di 10, quindi il volume è 36 x 10 x 1/3 = 120.

6. Ricorda di scrivere il risultato in unità cubiche. Le misure della piramide nell`esempio sono state date in centimetri, quindi il risultato deve essere scritto in centimetri cubi, 120 cm³. Se le misure sono state date in metri, scrivi la risposta in metri cubi (m³).
Metodo 5 di 6: Calcolo del volume di un cono

1. Scopri quali sono le proprietà di un cono. Un cono è una forma tridimensionale con una base circolare e un unico punto sulla faccia opposta. Un altro modo per vedere un cono è che è un tipo speciale di piramide a base circolare.
- Se la punta del cono è direttamente sopra il centro della base, si parla di cono diritto. Se non è direttamente sopra il centro, è chiamato cono obliquo. Fortunatamente, la formula per calcolare il volume è la stessa per entrambi i tipi di coni.

2. Conoscere la formula per calcolare il volume del cono. Questa formula è V = 1/3 x π x r² x h, dove r è il raggio del cerchio alla base, h è l`altezza del cono e π è la costante pi, che può essere arrotondata a 3,14.

3. Calcola l`area della base circolare del cono. Per fare ciò devi conoscere il raggio della base, che dovrebbe essere indicato sulla tua foto. Se hai il diametro invece del raggio, dividi quel numero per 2, perché il diametro è 2 volte il raggio (d = 2 x r). Quindi inserisci il raggio nella formula A = π x r² per calcolare l`area.

4. Trova l`altezza del cono. Questa è la distanza verticale dalla base del cono alla sommità. Nel nostro esempio, l`altezza del cono è di 5 cm.

5. Moltiplica l`altezza del cono per l`area della base. Nel nostro esempio, l`area della base è 28,27 cm² e l`altezza è 5 cm, quindi w x h = 28,27 x 5 = 141,35.

6. Ora moltiplica questo risultato per 1/3 (o dividi per 3) per ottenere il volume del cono. Nel passaggio precedente abbiamo effettivamente calcolato il volume di un cilindro, cioè un cono in cui le pareti sarebbero in posizione verticale e finirebbero in un altro cerchio. Dividendolo per 3 ottieni il volume del cono.

7. Ricorda di scrivere il risultato in unità cubiche. Il nostro cono è stato misurato in centimetri, quindi il volume dovrebbe essere espresso in centimetri cubi: 47,12 cm³.
Metodo 6 di 6: Calcolo del volume di una sfera

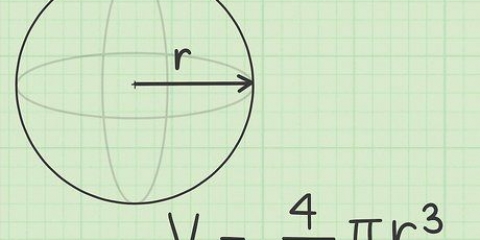
1. Riconosci una sfera. Una sfera è una forma tridimensionale perfettamente rotonda, in cui ogni punto della sua superficie è equidistante dal centro. In altre parole, è una palla.

2. Impara la formula per calcolare il volume di una sfera. La formula è V = 4/3 x π x r³ (cioè: "quattro terzi pi per r cubica"), dove r è il raggio della sfera e π è la costante pi (3.14).

3. Trova il raggio della sfera. Se il raggio è già indicato nell`immagine, è facile. Dato il diametro, dividi questo numero per 2 per ottenere il raggio. Il raggio della sfera in questo esempio è di 3 centimetri.

4. Misurare la sfera se il raggio non è specificato. Se devi misurare una sfera (come una pallina da tennis) per trovare il raggio, trova una corda abbastanza lunga da avvolgerla completamente. Quindi avvolgilo attorno all`oggetto nel punto più largo e segna il punto in cui la stringa si unisce. Quindi misura questa parte della corda con un righello per conoscere la circonferenza della sfera. Dividilo per 2 x π, o 6,28, quindi conosci il raggio.

5. Alza il raggio alla terza potenza per trovare r³. Elevare alla terza potenza significa semplicemente moltiplicare il numero tre volte per se stesso, quindi r³ = r x r x r. Nel nostro esempio r=3 diventa 3 x 3 x 3 = 27.

6. Moltiplica la tua risposta per 4/3. Puoi farlo con una calcolatrice o semplicemente farlo da solo e semplificare la frazione. Nel nostro esempio è 27 x 4/3 = 180/3 o 36.

7. Moltiplica il risultato per π per trovare il volume della sfera. L`ultimo passaggio nel calcolo del volume è moltiplicare il risultato ottenuto finora per π. Arrotonda π a due cifre decimali, è sufficiente per la maggior parte dei problemi di matematica (a meno che il tuo insegnante non dica diversamente), quindi moltiplicalo per 3,14 e avrai la tua risposta.

8. Scrivi la tua risposta in unità cubiche. Nel nostro esempio, abbiamo misurato in centimetri, quindi la risposta è V = 113,09 cm³.
Articoli sull'argomento "Calcola volume"
Condividi sui social network:
Popolare