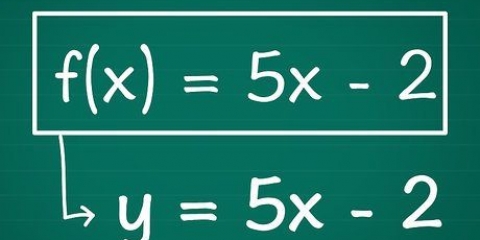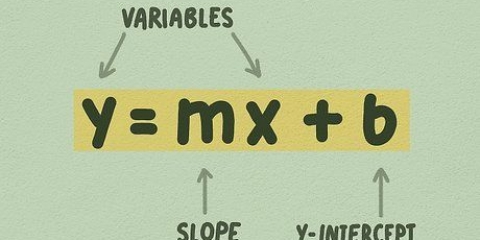Ad esempio: la funzione standard f(x) = 2x +16x + 39. Qui abbiamo a = 2, b = 16 e c = 39. Nella notazione dei vertici: f(x) = 4(x - 5) + 12. Qui abbiamo a = 4, h = 5 e k = 12. 
Esempio 1. (f(x) = 2x +16x + 39), h = -b/2a = -16/2(2). Risolvendo questo vediamo che h = -4. Esempio 2. (f(x) = 4(x - 5) + 12), vediamo subito che h = 5. 
Abbiamo visto ad esempio 1 che h = -4. Ora per trovare k risolviamo questa equazione inserendo questo valore di h nell`equazione, per la variabile x: k = 2(-4) + 16(-4) + 39. k = 2(16) - 64 + 39. k = 32 - 64 + 39 = 7 Dall`esempio 2 sappiamo che il valore di k è uguale a 12, senza bisogno di un calcolo. 
Nell`esempio 1, la parte superiore del grafico è (-4,7). Disegna il punto sul grafico e assicurati di nominare correttamente le coordinate. Nell`esempio 2, la parte superiore è (5,12). Quindi dal punto (0,0) vai 5 posti a destra e poi 12 in alto. 
Nel caso dell`esempio 1, l`asse di simmetria è la retta parallela all`asse y e passante per il punto(-4, 7). Sebbene non faccia parte della parabola stessa, evidenziare leggermente questa linea guida può mostrarti quanto sia simmetrica la curva della parabola. 
Nell`esempio 1 abbiamo a che fare con la funzione (f(x) = 2x +16x + 39), e questa è quindi una parabola di valle, perché a = 2 (positivo). Nell`esempio 2 abbiamo a che fare con la funzione f(x) = 4(x - 5) + 12), e anche questa è una parabola di valle perché a = 4 (positivo). 
Determina che f(x) = 0 e risolvi l`equazione. Questo metodo può funzionare per semplici equazioni quadratiche, specialmente nella forma dei vertici, ma scoprirai che diventa sempre più difficile man mano che le funzioni diventano più complesse. Di seguito sono riportati alcuni esempi. f(x) = 4(x - 12) 0 = 4(x - 12) - 4 4 = 4(x - 12) 1 = (x - 12) SqRt(1) = (x - 12) +/- 1 = x -12. x = 11 e 13 sono le intersezioni con l`asse x della parabola. Fattorizza l`equazione. Alcune equazioni della forma ax + bx + c possono essere facilmente riscritte come (dx + e)(fx +g), dove dx × fx = ax, (dx × g + fx × e) = bx, e e × g = C. In questo caso, le x-intercettazioni sono i valori di x dove ogni termine tra parentesi diventa 0. Ad esempio: x + 2 x + 1 = (x + 1)(x + 1) In questo caso, il punto di intersezione è uguale a -1 perché, compilato con entrambi i fattori, restituisce zero. Usa la formula abc. Se non è facile capire le intersezioni, o scomporre l`equazione, usa il "formula abc" che è appositamente progettato per questo. Assumiamo un`equazione nella forma ax + bx + c. Quindi inserisci i valori di a, b e c nella formula x = (-b +/- SqRt(b - 4ac))/2a. Nota che questo spesso ti dà due risposte per x, il che va bene - questo significa solo che la tua parabola ha due intersezioni con l`asse x. Ecco un esempio: -Inserisci 5x + 1x + 10 nell`equazione come segue: x = (-1 +/- SqRt(1 - 4(-5)(10)))/2(-5) x = (-1 +/- SqRt(1 + 200))/-10 x = (-1 +/- SqRt(201))/-10 x = (-1 +/- 14,18)/-10 x = (13.18/-10) e (-15.18/-10). Le intersezioni della parabola con l`asse x sono approssimativamente x = -1.318 e 1.518 Come nell`esempio 1 con l`equazione 2x + 16x + 39, questo sarà simile a questo: x = (-16 +/- SqRt(16 - 4(2)(39))))/2(2) x = (-16 +/- SqRt(256 - 312))/4 x = (-16 +/- SqRt(-56)/-10 Poiché non è possibile trovare la radice quadrata di un numero negativo, sappiamo che non esistono intersezioni con l`asse x per questa particolare parabola. 
Ad esempio, sappiamo che la nostra equazione quadratica 2x + 16x + 39 ha un punto di intersezione y = 39, ma possiamo anche trovarlo come segue: f(x) = 2x + 16x + 39 f(x) = 2(0) + 16(0) + 39 f(x) = 39. L`intersezione della parabola con l`asse y: y = 39. Come indicato sopra, possiamo leggere facilmente l`intersezione perché y = c. L`equazione 4(x - 5) + 12 ha un`intersezione con l`asse y che può essere trovata come segue: f(x) = 4(x - 5) + 12 f(x) = 4(0 - 5) + 12 f(x) = 4(-5) + 12 f(x) = 4(25) + 12 f(x) = 112. L`intersezione con l`asse y: y = 112. 
Diamo un`altra occhiata all`equazione x + 2x + 1. Sappiamo già che l`unica intersezione con l`asse x è (-1.0). Poiché a questo punto è tangente solo all`asse x, possiamo dedurre che il vertice del grafico è uguale a questo punto. Finora abbiamo solo un punto di questa parabola, non abbastanza per poter disegnare un grafico. Troviamo qualche punto in più per assicurarci di avere più valori. Proviamo a trovare i valori y associati ai seguenti valori x: 0, 1, -2 e -3. x=0: f(x) = (0) + 2(0) + 1 = 1. Allora il punto è (0.1). x=1: f(x) = (1) + 2(1) + 1 = 4. Allora il punto è (1,4). x=-2: f(x) = (-2) + 2(-2) + 1 = 1. Allora il punto è (-2.1). x=-3: f(x) = (-3) + 2(-3) + 1 = 4. Allora il punto è (-3,4). Posiziona questi punti nel grafico e disegna la tua parabola. Nota che la parabola è completamente simmetrica: se conosci i punti su un lato del grafico, di solito puoi risparmiare molto lavoro usando questi punti per trovare i punti sull`altro lato dell`asse di simmetria.
Rappresentazione grafica di una funzione
Come un grafico vede un`equazione quadratica ascia + bx + c, anche qualsiasi scritto comea(x - h) + k, sembra una curva a forma di U liscia. Questo è ciò che chiamiamo a parabola. Rappresentare graficamente un`equazione quadratica implica trovare il vertice, la direzione e spesso le intersezioni con l`asse x e l`asse y. Nel caso dell`equazione quadratica relativamente semplice, può anche essere sufficiente inserire un certo numero di valori per x per indicare questi punti nel sistema di coordinate, dopodiché si può disegnare la parabola. Procedi al passaggio 1 per iniziare.
Passi

1. Determina che tipo di equazione quadratica hai. Questo può essere scritto in due modi: la notazione standard e la notazione dei vertici (un altro modo per scrivere la formula della radice quadrata). Puoi usare entrambi per creare un grafico di un`equazione quadratica, ma questo processo è leggermente diverso in entrambi i casi. Di solito incontrerete la forma standard, ma di certo non fa male imparare ad usare entrambe le forme. Le due forme di un`equazione quadratica sono: La forma del vertice. Qui l`equazione quadratica è scritta come: f(x) = a(x - h) + k dove a, h e k sono numeri reali e a non è uguale a zero. Questa forma è chiamata vertice perché h e k si riferiscono direttamente al vertice della tua parabola nel punto (h,k). Due esempi di equazioni in forma di vertice sono f(x) = 9(x - 4) + 18 e -3(x - 5) + 1 Per poter fare un grafico di queste equazioni, determiniamo prima la parte superiore (h,k) del grafico. Nell`equazione standard puoi trovarlo tramite: h = -b/2a e k = f(h), mentre è già dato in forma di vertice perché h e k si verificano nell`equazione.
- La forma standard. Qui l`equazione quadratica è scritta come: f(x) = ax + bx + c dove a, b e c sono numeri reali e a non è uguale a zero.
- Due esempi di equazioni quadratiche standard: f(x) = x + 2x + 1 e f(x) = 9x + 10x -8.

2. Determina le tue variabili. Per risolvere un`equazione quadratica è solitamente necessario determinare le variabili a, b e c (o a, h e k). Un problema ordinario ti darà un`equazione quadratica nella forma standard, ma potrebbe verificarsi anche la notazione dei vertici.

3. Calcola h. Nella notazione dei vertici il valore di h è già dato, ma nella notazione standard questo valore deve ancora essere calcolato. Ricorda che per l`equazione standard, h = -b/2a.

4. Calcola k. Come per h, k è già noto per le equazioni nella forma dei vertici. Per le equazioni in notazione standard, ricorda che k = f(h). In altre parole, puoi trovare k sostituendo ogni variabile x con il valore di h.

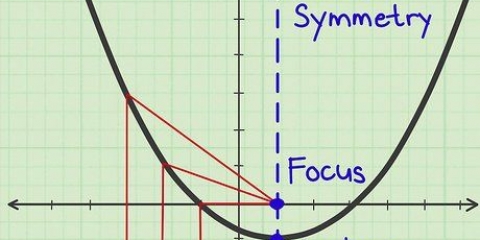
5. Disegna la parte superiore o inferiore del grafico. La cresta o la valle della tua parabola è il punto (h, k) - h rappresenta la coordinata x e k rappresenta la coordinata y. La cresta è il centro della tua parabola: il punto più alto o più basso, la cresta o la depressione, di un grafico a forma di "VOI" o vice versa. Essere in grado di determinare il vertice di una parabola è una parte essenziale per poter disegnare un grafico corretto – spesso determinare il vertice di una parabola fa parte di un problema di matematica a scuola.

6. Disegna l`asse di simmetria della parabola. L`asse di simmetria di una parabola è la retta che interseca la figura al centro e la divide esattamente a metà. Un lato del grafico è specchiato lungo questa linea nell`altro lato del grafico. Per equazioni quadratiche della forma ax + bx + c o a(x - h) + k, questo asse è la retta parallela all`asse y che passa per il vertice della parabola.

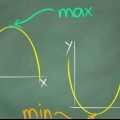
7. Determina la direzione della parabola. Dopo aver scoperto qual è la parte superiore della parabola, è necessario sapere se si tratta di una parabola di montagna o di una parabola di valle, ovvero se l`apertura è in basso o in alto. Fortunatamente questo è molto semplice. Se "un" positivo hai a che fare con una parabola a valle; è "un" negativo allora è una parabola di montagna (con l`apertura in basso)

8. Determinare, se necessario, le intersezioni della parabola. Spesso nei problemi di matematica ti viene chiesto di fornire le intersezioni della parabola con l`asse x (queste sono "zero", un o Due punti in cui la parabola interseca o tocca l`asse x). Anche se non richiesti, questi punti sono molto importanti per poter tracciare un grafico accurato. Ma non tutte le parabole si intersecano con l`asse x. Se hai a che fare con una parabola di valle e il punto di valle è sopra l`asse x o, nel caso di una parabola di montagna, appena sotto l`asse x, allora semplicemente non ci sono intersezioni da trovare. In tal caso, utilizzare uno dei seguenti metodi:

9. Se necessario, determinare l`intersezione della parabola con l`asse y. Spesso non è necessario, ma a volte è necessario trovare questo punto di intersezione, ad esempio per un problema di matematica. Questo è abbastanza semplice: imposta il valore di x su 0 e risolvi l`equazione per f(x) o y, che ti dà il valore y del punto in cui la parabola si interseca con l`asse y. La differenza con le intersezioni attraverso l`asse x è che con l`asse y c`è sempre un solo punto di intersezione. Nota: per le equazioni standard l`intersezione con l`asse y è a y = c.

10. Se lo ritieni necessario, disegna prima punti extra e poi l`intero grafico. Ora dovresti avere un picco o una valle, una direzione, intersezioni con l`asse x e possibilmente con l`asse y della tua equazione. Da questo punto puoi provare a disegnare la parabola usando questi punti oppure puoi provare a trovare più punti per rendere il grafico più accurato. Il modo più semplice per farlo è semplicemente compilare un numero di valori x, che restituisce un numero di valori y. Ti verrà spesso chiesto (dall`insegnante) di calcolare prima un numero di punti prima di poter disegnare la parabola.
Consigli
- Se necessario, arrotonda i numeri o usa le frazioni. Questo può aiutare a visualizzare correttamente un grafico.
- Si noti che se, per la funzione f(x) = ax + bx + c, b o c sono uguali a zero, quei termini scompariranno. Ad esempio, 12x + 0x + 6 equivale a 12x + 6 perché 0x equivale a 0.
Articoli sull'argomento "Rappresentazione grafica di una funzione"
Condividi sui social network:
Popolare