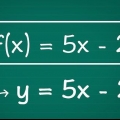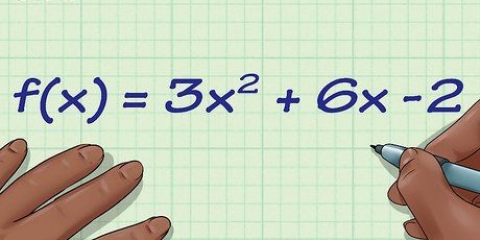sta diventando
sta diventando 
 sta diventando
sta diventando 
 sta diventando
sta diventando  .
.








Se i due risultati sono gli stessi, allora f(x)=f(-x) e la funzione originale è pari. Un esempio è:  e
e  .
.Questi due sono gli stessi e quindi la funzione è pari. Se ogni termine della nuova versione della funzione è il reciproco del termine corrispondente dell`originale, allora f(x)=-f(-x) e la funzione è dispari. Ad esempio:  ma
ma  .
.Nota che se moltiplichi ogni termine della prima funzione per -1, crei la seconda funzione. Quindi la funzione originale g(x) è dispari. Se la nuova funzione non corrisponde a nessuno di questi due esempi, non è né pari né dispari. Ad esempio:  ma
ma  . Il primo termine è lo stesso in ogni funzione, ma il secondo termine è un inverso. Pertanto, questa funzione non è né pari né dispari.
. Il primo termine è lo stesso in ogni funzione, ma il secondo termine è un inverso. Pertanto, questa funzione non è né pari né dispari.

È possibile verificare la simmetria selezionando i singoli punti. Se il valore y di qualsiasi valore x è uguale al valore y di -x, allora la funzione è pari. I punti scelti sopra per il tracciamento  dare i seguenti risultati:
dare i seguenti risultati: (1.3) e (-1.3) (2.9) e (-2.9). I valori y corrispondenti per x=1 e x=-1, e per x=2 e x=-2, indicano che questa è una funzione pari. Per un test migliore, selezionare due punti non è un`evidenza sufficiente, ma è una buona indicazione. 
Se scegli una coppia di valori di test per x e i loro valori corrispondenti inversi per -x, dovresti ottenere risultati inversi. Considera la caratteristica  . Questa funzione restituisce i seguenti punti:
. Questa funzione restituisce i seguenti punti:  . Il punto è (1,2).
. Il punto è (1,2). . Il punto è (-1,-2).
. Il punto è (-1,-2). . Il punto è (2,10).
. Il punto è (2,10). . Il punto è (-2,-10).
. Il punto è (-2,-10).Quindi f(x)=-f(-x), e puoi concludere che la funzione è dispari. 
Scegli una coppia di valori per x e -x, come segue:  . Il punto da tracciare è (1,4).
. Il punto da tracciare è (1,4). . Il punto da tracciare è (-1,-2).
. Il punto da tracciare è (-1,-2). . Il punto da tracciare è (2,10).
. Il punto da tracciare è (2,10). . Il punto da tracciare è (2,-2).
. Il punto da tracciare è (2,-2).Questo ti dà già abbastanza punti per notare che non c`è simmetria. I valori y per coppie opposte di valori x non sono gli stessi, né sono l`uno inverso dell`altro. Questa funzione non è né pari né dispari. Potresti vedere questa funzione,  , può essere riscritto come
, può essere riscritto come  . Scritta in questa forma, sembra una funzione pari perché c`è un solo esponente, ed è un numero pari. Tuttavia, questo esempio illustra che non è possibile determinare se una funzione è pari o dispari quando è racchiusa tra parentesi. Devi valutare la funzione in termini individuali e quindi esaminare gli esponenti.
. Scritta in questa forma, sembra una funzione pari perché c`è un solo esponente, ed è un numero pari. Tuttavia, questo esempio illustra che non è possibile determinare se una funzione è pari o dispari quando è racchiusa tra parentesi. Devi valutare la funzione in termini individuali e quindi esaminare gli esponenti.
Sapere se una funzione è pari o dispari
Contenuto
Un modo per classificare le funzioni è "pari", "dispari" o nessuno dei due. Questi termini si riferiscono alla ripetizione o alla simmetria della funzione. Il modo migliore per scoprirlo è manipolare algebricamente la funzione. Puoi anche studiare il grafico della funzione e cercare la simmetria. Una volta che sai come classificare le caratteristiche, puoi anche prevedere l`aspetto di determinate combinazioni di caratteristiche.
Passi
Metodo 1 di 2: test algebrico della funzione

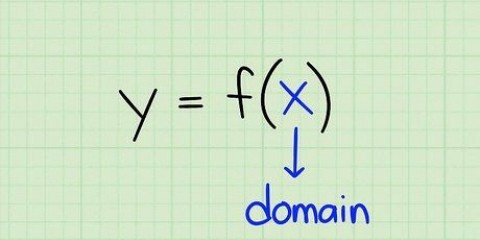
1. Visualizza variabili inverse. In algebra il reciproco di una variabile è negativo. Questo è vero o la variabile della funzione ora  è o qualcos`altro. Se la variabile della funzione originale è già negativa (o una sottrazione), allora il suo reciproco è positivo (o un`addizione). Di seguito sono riportati alcuni esempi di variabili e loro inversi:
è o qualcos`altro. Se la variabile della funzione originale è già negativa (o una sottrazione), allora il suo reciproco è positivo (o un`addizione). Di seguito sono riportati alcuni esempi di variabili e loro inversi:
 è o qualcos`altro. Se la variabile della funzione originale è già negativa (o una sottrazione), allora il suo reciproco è positivo (o un`addizione). Di seguito sono riportati alcuni esempi di variabili e loro inversi:
è o qualcos`altro. Se la variabile della funzione originale è già negativa (o una sottrazione), allora il suo reciproco è positivo (o un`addizione). Di seguito sono riportati alcuni esempi di variabili e loro inversi: - L`inverso di
è
- L`inverso di
è
- L`inverso di
è
.

2. Sostituisci ogni variabile della funzione con la sua inversa. Non modificare la funzione originale tranne il carattere. Ad esempio:
 sta diventando
sta diventando 
 sta diventando
sta diventando 
 sta diventando
sta diventando  .
.
3. Semplifica la nuova funzionalità. A questo punto non devi preoccuparti di risolvere la funzione per un dato valore numerico. Semplifichi semplicemente le variabili per confrontare la nuova funzione, f(-x), con la funzione originale, f(x). Ricorda le regole di base degli esponenti che dicono che una base negativa per una potenza pari sarà positiva, mentre una base negativa per una potenza dispari sarà negativa.








4. Confronta le due funzioni. Per ogni esempio che provi, confronta la versione semplificata di f(-x) con l`originale f(x). Metti i termini fianco a fianco per un facile confronto e confronta i segni di tutti i termini.
 e
e  .
. ma
ma  .
. ma
ma  . Il primo termine è lo stesso in ogni funzione, ma il secondo termine è un inverso. Pertanto, questa funzione non è né pari né dispari.
. Il primo termine è lo stesso in ogni funzione, ma il secondo termine è un inverso. Pertanto, questa funzione non è né pari né dispari.Metodo 2 di 2: testare la funzione graficamente

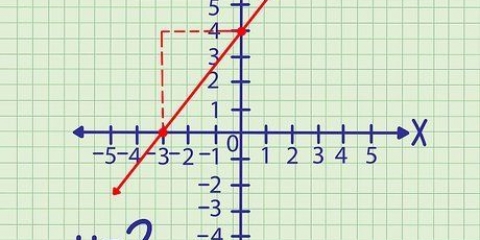
1. Grafico della funzione. Utilizzare carta millimetrata o una calcolatrice grafica per rappresentare graficamente la funzione. Scegli diversi valori numerici per  e inseriscilo nella funzione per ottenere il valore risultante di
e inseriscilo nella funzione per ottenere il valore risultante di  calcolare. Traccia questi punti sul grafico e dopo aver tracciato diversi punti traccia una linea attraverso di essi per rappresentare graficamente la funzione.
calcolare. Traccia questi punti sul grafico e dopo aver tracciato diversi punti traccia una linea attraverso di essi per rappresentare graficamente la funzione.
 e inseriscilo nella funzione per ottenere il valore risultante di
e inseriscilo nella funzione per ottenere il valore risultante di  calcolare. Traccia questi punti sul grafico e dopo aver tracciato diversi punti traccia una linea attraverso di essi per rappresentare graficamente la funzione.
calcolare. Traccia questi punti sul grafico e dopo aver tracciato diversi punti traccia una linea attraverso di essi per rappresentare graficamente la funzione. - Quando si tracciano i punti, prestare attenzione ai valori negativi positivi e corrispondenti per
. Ad esempio, se hai a che fare con la funzione
, quindi traccia i seguenti valori:
. Questo si traduce nel punto
.
. Questo si traduce nel punto
.
. Questo si traduce nel punto
.
. Questo si traduce nel punto
.

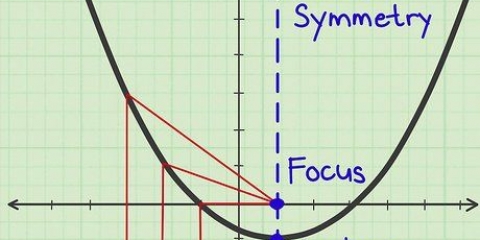
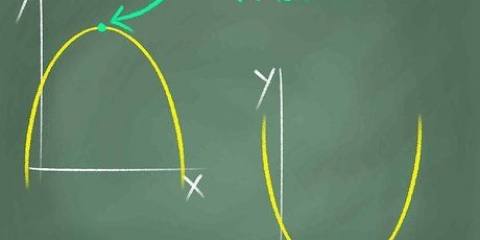
2. Nota la simmetria lungo l`asse y. Quando si osserva una funzione, la simmetria suggerisce un`immagine speculare. Se vedi che la parte del grafico sul lato destro (positivo) dell`asse y corrisponde alla parte del grafico sul lato sinistro (negativo) dell`asse y, allora il grafico è simmetrico rispetto all`asse yash. Se una funzione è simmetrica rispetto all`asse y, allora la funzione è pari.
 dare i seguenti risultati:
dare i seguenti risultati:
3. Verifica della simmetria dall`origine. L`origine è il punto centrale (0,0). La simmetria dell`origine significa che un risultato positivo per un valore x scelto corrisponderà a un risultato negativo per -x e viceversa. Le funzioni dispari mostrano la simmetria dell`origine.
 . Questa funzione restituisce i seguenti punti:
. Questa funzione restituisce i seguenti punti: . Il punto è (1,2).
. Il punto è (1,2). . Il punto è (-1,-2).
. Il punto è (-1,-2). . Il punto è (2,10).
. Il punto è (2,10). . Il punto è (-2,-10).
. Il punto è (-2,-10).
4. Vedi se non c`è simmetria. L`ultimo esempio è una funzione senza simmetria su entrambi i lati. Se guardi il grafico vedrai che non è un`immagine speculare né sull`asse y né attorno all`origine. Visualizza la funzione  .
.
 .
. . Il punto da tracciare è (1,4).
. Il punto da tracciare è (1,4). . Il punto da tracciare è (-1,-2).
. Il punto da tracciare è (-1,-2). . Il punto da tracciare è (2,10).
. Il punto da tracciare è (2,10). . Il punto da tracciare è (2,-2).
. Il punto da tracciare è (2,-2). , può essere riscritto come
, può essere riscritto come  . Scritta in questa forma, sembra una funzione pari perché c`è un solo esponente, ed è un numero pari. Tuttavia, questo esempio illustra che non è possibile determinare se una funzione è pari o dispari quando è racchiusa tra parentesi. Devi valutare la funzione in termini individuali e quindi esaminare gli esponenti.
. Scritta in questa forma, sembra una funzione pari perché c`è un solo esponente, ed è un numero pari. Tuttavia, questo esempio illustra che non è possibile determinare se una funzione è pari o dispari quando è racchiusa tra parentesi. Devi valutare la funzione in termini individuali e quindi esaminare gli esponenti.Consigli
- Se tutte le forme di una variabile nella funzione hanno esponenti pari, la funzione è pari. Se tutti gli esponenti sono dispari, la funzione è complessivamente dispari.
Avvertimento
- Questo articolo si applica solo alle funzioni con due variabili che possono essere rappresentate graficamente in un sistema di coordinate bidimensionale.
Articoli sull'argomento "Sapere se una funzione è pari o dispari"
Condividi sui social network:
Simile
Popolare