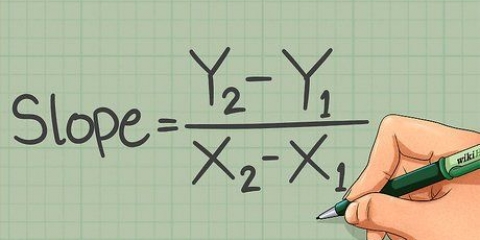Istruzioni passo passo gratis 
Se il coefficiente (pendenza) un nell`equazione è positivo, la parabola si apre verso l`alto (in una parabola orientata verticalmente), se la lettera maiuscola è `U` e il vertice è un minimo. Come la un negativo, la parabola si apre verso il basso e il vertice ha un massimo. Se hai problemi a ricordarlo, pensaci in questo modo: un`equazione con a positivo A sembra un sorriso; un confronto con a negativo a sembra un cipiglio. Diciamo che hai la seguente equazione: y = 2x -1. Questa parabola ha la forma di una "U" perché il un (2) è positivo. Se l`equazione ha un termine y invece di un termine x nella seconda potenza, la parabola sarà orientata orizzontalmente e aperta lateralmente (a destra oa sinistra), come una "C" o una "C" all`indietro. Ad esempio: la parabola y = x + 3 si apre a destra, come una `C`. 
Nell`esempio sopra (y = 2x² -1), .è a = 2 e b = 0`.` Ora puoi calcolare l`asse di simmetria inserendo i numeri:x = -0 / (2)(2) = 0`.` In questo caso, l`asse di simmetria è x = 0 (cioè l`asse y del sistema di coordinate). 
Le coordinate del vertice sono anche chiamate (h, k). In questo caso h uguale a 0 e K uguale a -1. L`equazione della parabola può essere scritta nella forma y = a(x - h)² + k. In questa forma, il vertice è il punto (h, k) e non è necessario fare alcun calcolo per trovare il vertice se non la corretta interpretazione del grafico. 
Il valore medio di x deve essere l`asse di simmetria nel caso di una parabola `verticale`. Devi includere almeno due valori sopra e sotto il valore medio di x nella tabella per la simmetria. In questo esempio si posiziona il valore dell`asse di simmetria (x = 0) al centro della tabella. 
Se x = -2, quindi y: y = (2) (-2) - 1 = 8 - 1 = 7 Se x = -1, quindi y: y = (2) (-1) - 1 = 2 - 1 = 1 Se x = 0, quindi y: y = (2) (0) - 1 = 0 - 1 = -1 Se x = 1, quindi y: y = (2) (1) - 1 = 2 - 1 = 1 Se x = 2, quindi y: y = (2) (2) - 1 = 8 - 1 = 7 
L`asse x è orizzontale, l`asse y è verticale. I numeri positivi sull`asse y sono sopra e i numeri negativi sotto il punto (0, 0). I numeri positivi sull`asse x sono a destra e i numeri negativi a sinistra del punto (0, 0). 
Disegna una parabola
Contenuto
Una parabola è una curva bidimensionale simmetrica speculare che ha la forma di un arco. Ogni punto della parabola è equidistante da un punto fisso (il fuoco) e da una retta fissa (la direttrice). Per mappare una parabola, devi trovare la parte superiore della parabola, così come alcuni punti su entrambi i lati, per segnare il percorso percorso dai punti.
Passi
Parte 1 di 2: Disegnare una parabola
1. Comprendere le parti di una parabola. Potresti ricevere alcune informazioni prima di iniziare e conoscere la terminologia ti aiuterà a evitare passaggi inutili. Ecco le parti della parabola che devi conoscere:
- La messa a fuoco. Un punto fisso all`interno della parabola che viene utilizzato per la definizione formale della curva.
- il regista. Una linea solida e dritta. La parabola è il luogo o insieme di punti in cui un dato punto è equidistante dal messa a fuoco e il direttrice si trova. (Vedi grafico sopra.)
- L`asse di simmetria. Questa è una retta passante per il vertice della parabola ed equidistante dai punti corrispondenti sui due bracci della parabola.
- il vertice. Il punto in cui l`asse di simmetria interseca la parabola è detto vertice della parabola. Se la parabola si apre o a destra, il vertice è a minimo della curva. Se la parabola si apre in basso oa sinistra, il vertice è a massimo.
2. Conosci l`equazione di una parabola. L`equazione generale di una parabola è y = ax+ bx + c. Può anche essere scritto in una forma ancora più generale y = a(x – h)² + k, ma qui ci concentreremo sulla prima forma dell`equazione.
3. Trova l`asse di simmetria. Ricorda che l`asse di simmetria è la retta che passa per il punto di svolta (vertice) della parabola. Nel caso di una parabola verticale (valle o montagna), l`asse è lo stesso della coordinata x del vertice, cioè il valore x del punto in cui l`asse di simmetria interseca la parabola. Usa questa formula per trovare l`asse di simmetria: x = -b/2a.
4. Trova il vertice. Una volta che conosci l`asse di simmetria, puoi inserire quel valore per x per ottenere la coordinata y. Queste due coordinate ti danno il vertice della parabola. In questo caso, sostituisci 0 con 2x -1 per ottenere la coordinata y. y = 2 x 0 -1 = 0 -1 = -1. Il vertice è (0,-1) e la parabola interseca l`asse y a -1.
5. Crea una tabella di valori per x. Crea una tabella con determinati valori per x nella prima colonna. Questa tabella fornisce le coordinate necessarie per rappresentare graficamente l`equazione.
6. Calcola i valori delle coordinate y corrispondenti. Sostituisci qualsiasi valore di x nell`equazione della parabola e calcola i valori corrispondenti di y. Metti questi valori calcolati di y nella tabella. In questo esempio, i valori di y sono calcolati come segue:
7. Inserisci i valori calcolati di y nella tabella. Ora hai trovato almeno cinque coppie di coordinate per la parabola e sei quasi pronto per disegnare la parabola. In base al tuo lavoro, ora hai i seguenti punti: (-2, 7), (-1, 1), (0, -1), (1, 1), (2, 7). Ricordiamo che la parabola (simmetrica) è rappresentata rispetto all`asse di simmetria. Ciò significa che le coordinate y dei punti direttamente opposti rispetto all`asse di simmetria saranno uguali. Le coordinate y associate alle coordinate x -2 e +2 sono entrambe 7; le coordinate y appartenenti alle coordinate x -1 e +1 sono entrambe 1, e così via.
8. Disegna i punti della tabella nel sistema di coordinate. Ogni riga della tabella forma una coppia di coordinate (x, y) sul sistema di coordinate. Disegna tutti i punti usando le coordinate nella tabella.
9. Unisci i punti. Per rappresentare graficamente la parabola, collegare i punti disegnati nel passaggio precedente. Il grafico in questo esempio ha l`aspetto di una U. Collega i punti usando linee leggermente curve (piuttosto che rette). Questo crea l`immagine più accurata della parabola (che è leggermente curva su tutta la sua lunghezza). Alle due estremità della parabola puoi disegnare frecce che puntano lontano dal vertice, se lo desideri. Ciò indica che la parabola continua all`infinito.
Parte 2 di 2: Spostamento del grafico di una parabola
Se si desidera un modo più rapido per spostare una parabola senza dover ritrovare il suo vertice e specificare nuovamente i diversi punti della parabola, è necessario comprendere l`equazione di una parabola e imparare a convertirla verticalmente o orizzontalmente. Inizia con la parabola di base: y = x. Ha un vertice nel punto (0, 0) ed è una parabola di valle. Alcuni punti del grafico sono: (-1, 1), (1, 1), (-2, 4) e (2, 4). Puoi spostare una parabola in base all`equazione.
1. Sposta una parabola verso l`alto. Considera l`equazione y = x +1. Questo sposta la parabola originale verso l`alto di un`unità. Il vertice è ora (0, 1) invece di (0, 0). La sua forma non è cambiata, ma ciascuna coordinata y verrà spostata in alto di un`unità. Quindi, invece di (-1, 1) e (1, 1), disegniamo i punti (-1, 2) e (1, 2).
2. Sposta una parabola verso il basso. Prendi l`equazione y = x -1. Spostiamo la parabola originale verso il basso di un`unità in modo che il vertice sia ora (0, -1) invece di (0, 0,). Avrà ancora la stessa forma della parabola originale, ma ciascuna coordinata y verrà spostata verso il basso di un`unità. Quindi, invece di (-1, 1) e (1, 1), ad esempio, disegniamo (-1, 0) e (1, 0).
3. Sposta una parabola a sinistra. Considera l`equazione y = (x + 1). Questo sposta la parabola originale di un`unità a sinistra. Il vertice è ora (-1, 0) invece di (0, 0). La forma della parabola originale rimane la stessa, ma ciascuna coordinata x viene spostata di una a sinistra. Ad esempio, invece di (-1, 1) e (1, 1), disegniamo (-2, 1) e (0, 1).
4. Sposta una parabola a destra. Considera l`equazione y = (x - 1). Questa è la parabola originale spostata di un`unità a destra. Il vertice è ora (1, 0) invece di (0, 0). La forma della parabola originale rimane la stessa, ma ogni coordinata x viene spostata di un punto a destra. Ad esempio, invece di (-1, 1) e (1, 1), disegniamo (0, 1) e (2, 1).
Articoli sull'argomento "Disegna una parabola"
Condividi sui social network:
Simile
Popolare
