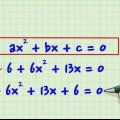Istruzioni passo passo gratis 
Ad esempio, nell`equazione quadratica -8a + 24a + 144, ogni costante è un multiplo di 8, quindi 8 può essere posto fuori parentesi, dando -8(a - 3a - 18). Anche se il coefficiente -3 e la costante -18 sono entrambi divisibili per -3, il coefficiente 1 del primo termine non lo è, quindi non possiamo fattorizzare ulteriormente. Nell`equazione quadratica - x - 2x - 1, ogni termine è divisibile per -1, che dopo la fattorizzazione può essere scritto come (-1)(x + 2x + 1). 
Nell`esempio, x + 6x + 5, 5 * 1 = 5 e 5 + 1 = 6. Quindi, la soluzione è (x + 1)(x + 5). Se non tutti i termini nell`equazione quadratica sono positivi, non dimenticare di considerare i numeri negativi. Ad esempio, x - 3x - 18 fattore in (x - 6)(x + 3) perché -6 + 3 = -3 e -6 * 3 = -18. Inizia facendo un elenco di tutti i possibili fattori di a e c. Quindi controlla quale coppia di fattori funziona, utilizzando i vincoli come indicato sopra. Ad esempio, prendi 3x + 10x + 8. Le possibili coppie di fattori di 3 sono 1 * 3. Possibili coppie di fattori di 8 sono 1 * 8 e 2 * 4. Poiché 3 * 1 = 3 (il termine dell`equazione quadratica), 1 * 4 + 2 * 3= 10 (il termine b) e 2 * 4 = 8 (il termine c), la soluzione è (3x + 4) ( x + 2). 
(x + a) diventa x + 2ax + a. Ad esempio, (x + 3) = x + 6x + 9 e (3x + 2) = 9x + 12x + 4. Allo stesso modo, (x - a) diventa x - 2ax + a. Ad esempio, (x - 3) = x - 6x + 9. 
(x + a)(x - a) diventa x - a. Quindi x - 9 può essere rapidamente calcolato in (x + 3)(x - 3) e 4x - 4 = (2x + 2)(2x - 2). 
Inizia con b - 4ac, che è 5 - 4(1)(6) = 1. La radice quadrata di 1 è 1. Termina risolvendo l`equazione. -b + 1 = -5 + 1 = -4. Dividi questo per 2a (2 * 1 = 2) per ottenere -2 come risposta. Nota che se avessimo scomposto questa equazione, invece di usare la formula abc, avremmo avuto come risposta (x + 2)(x + 3). Se imposti questa equazione uguale a 0, ottieni due soluzioni, x = 2 e x = -3, che abbiamo trovato anche con la formula. 
Puoi fattorizzare polinomi di più variabili usando i metodi sopra se sono equazioni quadratiche che presuppongono una variabile. Ad esempio, prendi 4xy - 5x + 15y. Questo può essere riscritto come (4x)y + 15y - 5x. Nota che questo si adatta alla forma ax + bx + c, dove a = 4x e c = 5x. Questa equazione può quindi essere risolta con la formula abc. Puoi esercitarti sulla fattorizzazione delle equazioni quadratiche facendo problemi in un libro che tratta di algebra.
Fattorizzare
Contenuto
In Algebra, un`equazione quadratica è un polinomio costituito da 3 termini, della forma ax + bx + c. I polinomi hanno molte applicazioni in matematica e scienze e la risoluzione di equazioni quadratiche è un`abilità importante. Mentre la maggior parte delle equazioni quadratiche può essere semplicemente scomposta, ci sono diversi casi in cui un`equazione quadratica deve essere scomposta in un modo speciale.Se nessuno dei metodi nella seguente guida è utile, potrebbe essere necessario utilizzare metodi per la fattorizzazione di polinomi superiori.
Passi
Metodo 1 di 4: Divisione Due
1. Ordina gli argomenti dell`equazione quadratica dal più grande al più piccolo. Un argomento è una variabile nel polinomio; l`ordine normale di collocamento dei termini va dalla potenza più alta alla più bassa. Quindi, 5 + x + 6x devono essere ordinati come x + 6x + 5.
2. Escludi ogni fattore che si verifica in tutti e tre i termini. Se le costanti dell`equazione quadratica sono tutte multiple dello stesso numero, puoi metterle fuori parentesi, o se ogni componente dell`equazione quadratica ha una variabile uguale, allora quella variabile può essere posta fuori parentesi.
3. Cerca schemi che semplifichino la risoluzione di un`equazione quadratica. Per informazioni ed esempi sempre più dettagliati, vedere il metodo per la risoluzione di casi speciali di un`equazione quadratica.
4. Se possibile, prova a dividere l`equazione quadratica in 2 due termini della forma (mx + n)(qx + r). Spesso si tratta solo di provare ciò che funziona, ma ci sono trucchi che lo rendono più facile. Assumiamo innanzitutto che il primo termine nell`equazione quadratica (il termine x) sia uguale a 1 (il termine assomiglia più a x che ad es., 3x). I valori m e q dei due termini sono 1, quindi la tua soluzione sarà simile a (x + b)(x + d). Quindi trova per la tua equazione della forma ax + bx + c, i valori n e r tali che: n * r = c e n + r = b.
5. Se la costante nel primo termine non è uguale a 1 (es. se assomiglia più a 3x che a x), la fattorizzazione diventa un po` più difficile e tramite ax + bx + c ottieni finalmente una soluzione nella forma (mx + n)(qx + r). Per una soluzione corretta, m * q = a, m * r + n * q = b e n * r = c.
Metodo 2 di 4: Factoring di casi speciali
1. Controlla se la costante nel primo o nel terzo termine dell`equazione è primo. Un numero primo è divisibile solo per se stesso e 1. Ciò riduce il numero di possibili fattori binomiali. Nell`esempio precedente: x + 6x + 5 c`è solo 1 possibile insieme di fattori binomiali, (x + 5)(x + 1), perché 5 è primo.
2. Controlla se l`equazione quadratica è un quadrato perfetto. Ciò richiede che i valori dei coefficienti a e c dell`equazione ax + bx + c siano quadrati perfetti (e positivi!), e che il valore di b è doppio del valore del prodotto della radice quadrata di a e c.
3. Per alcune equazioni quadratiche della forma x - n:
Metodo 3 di 4: utilizzo della formula abc
Per le equazioni quadratiche della forma ax + bx + c che sono difficili o impossibili da risolvere, utilizzare la formula abc.
1. Impara a usare la formula abc.
2. Immettere a, b e c e risolvere la prima parte della formula. Supponiamo di avere l`equazione quadratica x + 5x + 6.
3. Risolvi l`altra parte. Sappiamo già che la radice quadrata di b - 4ac = 1. -b - 1 = -6. Dividi questo per 2a (2) per ottenere -3.
4. Controlla le tue soluzioni compilandole per x. A volte una o più delle risposte non sono soluzioni valide (ad esempio se sono numeri immaginari). Ma se un`equazione quadratica ha una soluzione, l`equazione la troverà.
Metodo 4 di 4: Il quadrato nascosto in un polinomio
Alcune equazioni quadratiche sono di ordine superiore, ma essenzialmente solo quadratiche. Una volta riconosciuti come tali, puoi trattarli come tali usando la sostituzione.
1. Osserva le variabili in ogni termine.Ad esempio, x - 7x + 12 sembra essere una potenza di 6, ma dopo la sostituzione di u=x, questa diventa u - 7u + 12. Questo ti lascia con un`equazione che è molto più facile da risolvere.
- Sostituzioni più complesse possono aiutare a risolvere problemi più complicati. Ad esempio, xy - 7xy + 12y è semplificato in xy(u - 7u + 12) e dopo la sostituzione u = x/y. Tale sostituzione è possibile ogniqualvolta la somma dei poteri dei due termini è doppia della potenza del restante termine.
2. Se tale sostituzione può aver luogo, scomporre il polinomio semplice, in questo caso, u - 7u + 12 = (u-3)(u-4)
3. Annulla la sostituzione e applica x alla soluzione. Quindi, sostituisci u con x , x - 7x + 12 = (x - 3)(x - 4). Se possibile o desiderato, ogni fattore può essere ulteriormente semplificato.
Consigli
- Utilizzare il criterio di Eisenstein per determinare rapidamente se un polinomio è non riducibile e non fattorizzabile. Questo criterio si applica a qualsiasi polinomio, ma soprattutto a un`equazione quadratica. Se esiste un numero primo p che rende divisibili gli ultimi due termini e soddisfa le seguenti condizioni, allora il polinomio non può essere ridotto:
- Il termine costante (la c in un`equazione quadratica della forma ax + bx + c) è un plurale di p ma non di p.
- Il primo termine (qui, a) non è un plurale di p.
- Ad esempio, 14x + 45x + 51 è irriducibile perché ha un numero primo (3) che rende divisibili sia 45 che 51, ma non 14 e 51, che non sono divisibili per 3.
Avvertenze
- Sebbene vere per i quadrati, le equazioni quadratiche che possono essere fattorizzate non sono necessariamente il prodotto di due binari. Un controesempio è x + 105x + 46 = (x + 5x + 2)(x - 5x + 23).
Necessità
- Libro di algebra/matematica
- Carta e matita
Articoli sull'argomento "Fattorizzare"
Condividi sui social network:
Popolare
