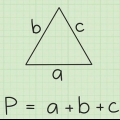a + b > C = 17 > 5 a + c > B = 12 > 10 b + c > un = 15 > 7 
5+8 > 3 = 13 > 3, quindi questo lato è corretto. 5+3 > 8 = 8 > 8. Perché questo non è giusto, puoi fermarti ora. Questo non è un triangolo.
Determina se tre lunghezze insieme formano un triangolo
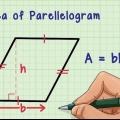
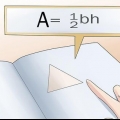
Determinare se le lunghezze di tre lati insieme formano un triangolo è più facile di quanto sembri. Tutto quello che devi fare è usare il teorema della disuguaglianza triangolare, che afferma che la somma delle lunghezze di due lati di un triangolo è sempre maggiore del terzo lato. Se questo vale per tutte e tre le combinazioni delle lunghezze aggiunte, allora hai a che fare con un triangolo.
Passi

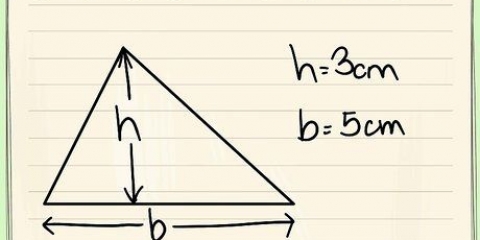
1. Impara il teorema della disuguaglianza triangolare. Questo teorema afferma che la somma dei due lati di un triangolo deve essere maggiore del terzo lato. Se questo si applica a tutte e tre le combinazioni, allora hai un vero triangolo. Dovrai controllare queste combinazioni, una per una, per assicurarti che si possa formare un triangolo. Puoi anche considerare il triangolo come i lati delle lunghezze a, b e c e il teorema come disuguaglianza: a+b > c, a+c > b e b+c > un.
- Un esempio, un = 7, B = 10 e C = 5.

2. Controlla se la somma dei primi due lati è maggiore del terzo. In questo caso puoi usare i lati un e B somma insieme, cioè 7 + 10, per ottenere 17, che è maggiore di 5. Puoi anche pensarlo come 17 > 5.

3. Controlla se la somma della successiva combinazione di due lati è maggiore del lato rimanente. Bene, guarda solo se la somma dei lati un e C è maggiore del lato B. Ciò significa che devi vedere se 7 + 5, o 12, è maggiore di 10. 12 > 10, quindi è giusto.

4. Controlla se la somma dell`ultima combinazione di due lati è maggiore del lato rimanente. Dovrai controllare se la somma dei lati B e seta C è maggiore della seta un. Per fare ciò, dovrai controllare se 10 + 5 è maggiore di 7. 10 + 5 = 15 e 15 > 7, quindi il triangolo è corretto per tutti i lati.

5. Controlla il tuo lavoro. Ora che hai controllato tutti i lati uno per uno, puoi controllare di nuovo che la regola si applica a tutte e tre le combinazioni. Se la somma di uno dei due lati è maggiore del terzo in qualsiasi combinazione, come con questo triangolo, allora hai determinato che il triangolo è valido. Se la regola non vale nemmeno per una combinazione, allora non è un vero triangolo. Poiché le seguenti affermazioni sono vere, hai trovato un triangolo valido:

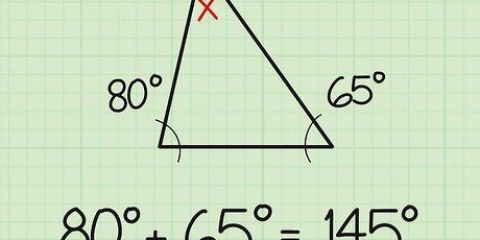
6. Sapere come scoprire un triangolo non valido. Giusto per prendere la mano, ma devi assicurarti di poter individuare un triangolo che non è giusto. Supponiamo di avere a che fare con i seguenti tre lati e le lunghezze: 5, 8 e 3. Vediamo se superano il test:
Consigli
- Questo vale sempre, purché non si commettano errori di calcolo e se si tratta di un`aggiunta regolare, è molto semplice.
Articoli sull'argomento "Determina se tre lunghezze insieme formano un triangolo"
Condividi sui social network:
Simile
Popolare