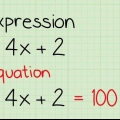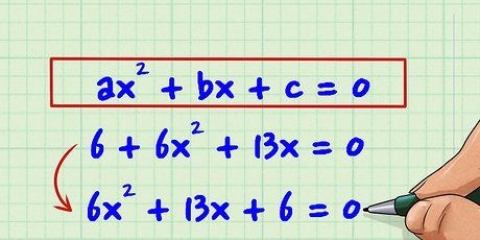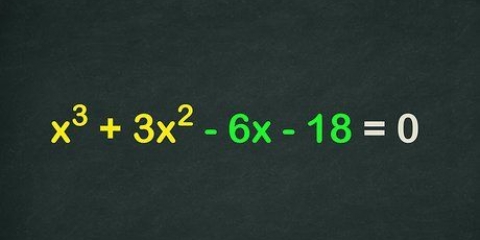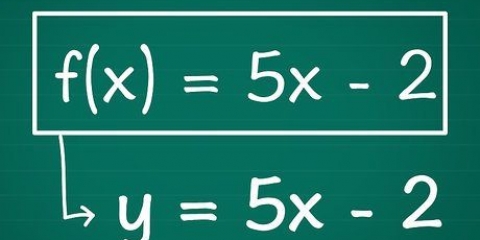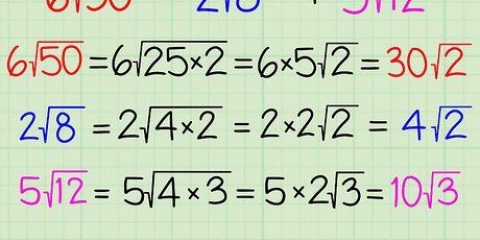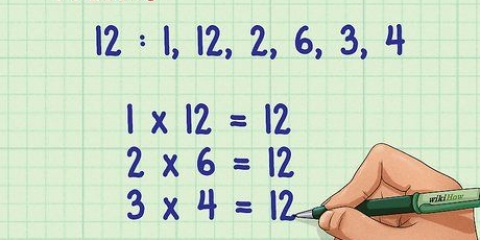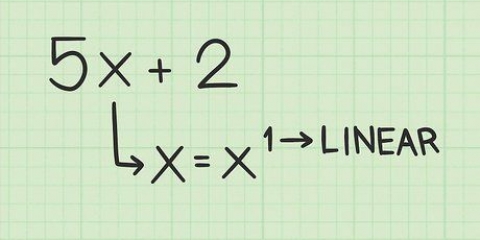→
→ 
 →
→ 
 →
→ 
Nota come i segni meno rimangono davanti al 2. Quando un termine viene sottratto, il segno meno rimane davanti ad esso. 
Compito dell`esercizio: .
. Fattori di 3:1, 3 Fattori di 6: 1, 2, 3, 6. `Il massimo comun divisore è 3`. 
Compito dell`esercizio: .
. Trova i massimi comun divisori: 3 Per rimuovere il fattore da entrambi i termini:

Compito dell`esercizio:
Trova i massimi comun divisori: 3 Per rimuovere il fattore da entrambi i termini:
Moltiplica il fattore per una nuova espressione:
Risposta finale sciolta: 

Per riordinare i termini:
Trovare il massimo comun divisore:
Per rimuovere il fattore da entrambi i termini:
Moltiplica il fattore per una nuova espressione:
Controlla la risposta:


Compito dell`esercizio:
Uguale a zero:


Compito dell`esercizio:
Uguale a zero:
Sciogliere:

Compito dell`esercizio:
Uguale a zero:
Sciogliere:
Rendi entrambi i termini uguali a zero 0: 




y = 0 

y = 4 


 Questa risposta è corretta
Questa risposta è corretta

 Anche questa risposta è corretta.
Anche questa risposta è corretta.

Incarico originale:
Per riordinare i termini:
Per unire termini simili:
Trova i massimi comun divisori:
Sciogliere:

La formula per la differenza dei quadrati perfetti:
Compito dell`esercizio:
Determina le radici quadrate: 

Applicare le radici quadrate alla formula: 

Formula per la differenza delle terze potenze:
Compito dell`esercizio:
Determina le radici del cubo: ![Binomi di factoring {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Binomi di factoring {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Applicare i cubi alla formula: 

Formula per la somma dei cubi perfetti:
Compito dell`esercizio:
Determina le radici del cubo: ![Binomi di factoring {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Binomi di factoring {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Applica i cubi alla formula: 
Binomi di factoring
Contenuto
In algebra, i binomi sono espressioni di due termini collegate da un segno più o meno, ad esempio 
Passi
Parte 1 di 3: Factoring Binomi

1. Ripassa di nuovo le basi del factoring. Il factoring sta dividendo un gran numero nei suoi divisori più semplici. Ognuna di queste parti è chiamata `fattore`. Ad esempio, il numero 6 è divisibile per quattro numeri diversi: 1, 2, 3 e 6. Quindi 1, 2, 3 e 6 sono i fattori di 6.
- I fattori di 32 sono 1, 2, 4, 8, 16 e 32
- Sia `1` che il numero che fattorizzi sono sempre fattori. Quindi i fattori di un numero piccolo come 3 sono solo 1 e 3.
- I fattori sono solo quei numeri che sono completamente divisibili, cioè i numeri "interi". Potresti dividere 32 per 3,564 o 21,4952, ma quelli non sono fattori, solo numeri decimali.

2. Elenca i termini del binomio per facilitarne la lettura. Un binomio non è altro che l`addizione o la sottrazione di due termini, almeno uno dei quali contiene una variabile. A volte queste variabili hanno esponenti, come  o
o  . Se stai cercando di fattorizzare i binomi per la prima volta, è utile ordinare le equazioni in termini di variabili discendenti, il che significa che l`esponente più grande viene per ultimo. Ad esempio:
. Se stai cercando di fattorizzare i binomi per la prima volta, è utile ordinare le equazioni in termini di variabili discendenti, il che significa che l`esponente più grande viene per ultimo. Ad esempio:
 o
o  . Se stai cercando di fattorizzare i binomi per la prima volta, è utile ordinare le equazioni in termini di variabili discendenti, il che significa che l`esponente più grande viene per ultimo. Ad esempio:
. Se stai cercando di fattorizzare i binomi per la prima volta, è utile ordinare le equazioni in termini di variabili discendenti, il che significa che l`esponente più grande viene per ultimo. Ad esempio: →
→ 
 →
→ 
 →
→ 

3. Trova il massimo comun divisore di entrambi i termini. Ciò significa che stai cercando il numero più grande per cui entrambe le parti del binomio sono divisibili. Se questo non funziona, fattorizza entrambi i numeri da soli e guarda qual è il numero corrispondente più alto. Ad esempio:
 .
.
4. Dividi il massimo comun divisore per ogni termine. Se conosci il denominatore comune, devi rimuoverlo da ogni termine. Nota che dividi semplicemente i termini rendendo ciascuno un problema di divisione più piccolo. Se eseguite correttamente, entrambe le equazioni hanno lo stesso fattore:
 .
.

5. Moltiplica il tuo fattore per l`espressione risultante per arrotondare. Nell`ultimo problema hai rimosso un 3 e ottieni  . Ma non vuoi eliminare completamente i 3, considerali solo per semplificare le cose. Non puoi semplicemente cancellare i numeri senza reinserirli! Moltiplica il fattore per l`espressione per completare questa sezione. Ad esempio:
. Ma non vuoi eliminare completamente i 3, considerali solo per semplificare le cose. Non puoi semplicemente cancellare i numeri senza reinserirli! Moltiplica il fattore per l`espressione per completare questa sezione. Ad esempio:
 . Ma non vuoi eliminare completamente i 3, considerali solo per semplificare le cose. Non puoi semplicemente cancellare i numeri senza reinserirli! Moltiplica il fattore per l`espressione per completare questa sezione. Ad esempio:
. Ma non vuoi eliminare completamente i 3, considerali solo per semplificare le cose. Non puoi semplicemente cancellare i numeri senza reinserirli! Moltiplica il fattore per l`espressione per completare questa sezione. Ad esempio:




6. Controlla il tuo lavoro moltiplicando per l`equazione originale. Se hai fatto tutto bene, è facile verificare se l`hai fatto bene. Moltiplica il tuo fattore per entrambi i singoli termini tra parentesi. Se corrisponde al binomio originale dato, allora hai fatto tutto bene. Dall`inizio alla fine risolviamo l`espressione  avanti per esercitarsi:
avanti per esercitarsi:
 avanti per esercitarsi:
avanti per esercitarsi:




Parte 2 di 3: Fattorizzazione di binomi per risolvere equazioni

1. Fattore per semplificare le equazioni in modo che siano più facili da risolvere. Quando si risolve un`equazione con binomi, in particolare binomi complessi, può sembrare che non ci sia modo di far combaciare tutto. Ad esempio, prova a risolvere quanto segue:  . Un modo per farlo, specialmente con gli esponenti, è quello di fattorizzare prima.
. Un modo per farlo, specialmente con gli esponenti, è quello di fattorizzare prima.
 . Un modo per farlo, specialmente con gli esponenti, è quello di fattorizzare prima.
. Un modo per farlo, specialmente con gli esponenti, è quello di fattorizzare prima. - Compito dell`esercizio:
- Ricorda che i binomi possono avere solo due termini. Se ci sono più di due termini, devi impara a risolvere i polinomi.

2. Somma e sottrai in modo che un lato dell`equazione sia uguale a zero. L`intera strategia si basa su uno dei fatti fondamentali della matematica: qualcosa moltiplicato per zero deve essere uguale a zero. Quindi, se la tua equazione è uguale a zero, uno dei termini fattorizzati deve essere uguale a zero! Per iniziare, dovrai sommare e sottrarre in modo che un lato sia uguale a zero.




3. Sciogli il lato diverso da zero come sei abituato. A questo punto stai solo fingendo che l`altro lato non esista. Trova il massimo comun divisore, dividilo, quindi crea la tua espressione fattorizzata.




4. Imposta i termini dentro e fuori le parentesi uguali a zero. Nel problema pratico moltiplichi 2y per (4 – y), e questo deve essere uguale a zero. Poiché qualcosa moltiplicato per zero è uguale a zero, ciò significa che 2y o (4 – y) deve essere uguale a zero. Crea due equazioni separate per scoprire quale valore deve avere y per rendere entrambi i lati uguali a zero.






5. Risolvi entrambe le equazioni per zero per la risposta o le risposte finali. Puoi ottenere una o più risposte. Ricorda, solo un lato deve essere uguale a zero, quindi puoi ottenere alcuni valori diversi per y che risolvono la stessa equazione. Gli ultimi passi dell`esercitazione:





6. Applica le tue risposte all`equazione originale per assicurarti che siano corrette. Una volta che hai trovato i valori giusti per y, dovresti essere in grado di usarli per risolvere l`equazione. Questo è semplice come provare ogni valore di y invece della variabile come mostrato di seguito. Le risposte sono y = 0 e y = 4, quindi:


 Questa risposta è corretta
Questa risposta è corretta

 Anche questa risposta è corretta.
Anche questa risposta è corretta.Parte 3 di 3: Affrontare problemi più difficili

1. Ricorda che le variabili contano come fattori, anche con esponenti. Ricorda che la fattorizzazione riguarda la determinazione di quali numeri rientrano nell`intero. L`espressione  è un altro modo di dire
è un altro modo di dire  . Ciò significa che puoi inserire qualsiasi x fuori parentesi se anche l`altro termine ne ha una. Tratta le variabili come numeri regolari. Ad esempio:
. Ciò significa che puoi inserire qualsiasi x fuori parentesi se anche l`altro termine ne ha una. Tratta le variabili come numeri regolari. Ad esempio:
 è un altro modo di dire
è un altro modo di dire  . Ciò significa che puoi inserire qualsiasi x fuori parentesi se anche l`altro termine ne ha una. Tratta le variabili come numeri regolari. Ad esempio:
. Ciò significa che puoi inserire qualsiasi x fuori parentesi se anche l`altro termine ne ha una. Tratta le variabili come numeri regolari. Ad esempio: può essere scomposto, perché entrambi i termini contengono una t. La risposta finale sarà
- Puoi anche inserire più variabili al di fuori delle parentesi contemporaneamente. Ad esempio, nel
entrambi i termini contengono lo stesso
. Puoi dissolverlo

2. Riconoscere binomi non ancora semplificati combinando termini simili. Prendi, ad esempio, l`espressione  . Qui sembra che tu abbia a che fare con quattro termini, ma se guardi più da vicino ti accorgerai che ce ne sono solo due. Puoi aggiungere termini simili e poiché sia 6 che 14 non hanno variabili e 2x e 3x condividono la stessa variabile, possono essere uniti. La dissoluzione è quindi facile:
. Qui sembra che tu abbia a che fare con quattro termini, ma se guardi più da vicino ti accorgerai che ce ne sono solo due. Puoi aggiungere termini simili e poiché sia 6 che 14 non hanno variabili e 2x e 3x condividono la stessa variabile, possono essere uniti. La dissoluzione è quindi facile:
 . Qui sembra che tu abbia a che fare con quattro termini, ma se guardi più da vicino ti accorgerai che ce ne sono solo due. Puoi aggiungere termini simili e poiché sia 6 che 14 non hanno variabili e 2x e 3x condividono la stessa variabile, possono essere uniti. La dissoluzione è quindi facile:
. Qui sembra che tu abbia a che fare con quattro termini, ma se guardi più da vicino ti accorgerai che ce ne sono solo due. Puoi aggiungere termini simili e poiché sia 6 che 14 non hanno variabili e 2x e 3x condividono la stessa variabile, possono essere uniti. La dissoluzione è quindi facile:





3. Riconosci la speciale "differenza dei quadrati perfetti". Un quadrato perfetto è un numero la cui radice è un intero, ad esempio 
 ,
, 
 , o anche
, o anche 
 Se il tuo binomio è una somma meno con due quadrati perfetti, come
Se il tuo binomio è una somma meno con due quadrati perfetti, come  , quindi puoi semplicemente usarli in questa formula:
, quindi puoi semplicemente usarli in questa formula:

 ,
, 
 , o anche
, o anche 
 Se il tuo binomio è una somma meno con due quadrati perfetti, come
Se il tuo binomio è una somma meno con due quadrati perfetti, come  , quindi puoi semplicemente usarli in questa formula:
, quindi puoi semplicemente usarli in questa formula:





4. Impara a semplificare la "differenza dei cubi perfetti". Come i quadrati perfetti, questa è una formula semplice in cui due cubi vengono sottratti l`uno dall`altro. Ad esempio,  . Come prima, trova la radice cubica di ciascuno e usala nella formula:
. Come prima, trova la radice cubica di ciascuno e usala nella formula:
 . Come prima, trova la radice cubica di ciascuno e usala nella formula:
. Come prima, trova la radice cubica di ciascuno e usala nella formula:

![Binomi di factoring {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Binomi di factoring {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)


5. Sappi che la somma dei cubi perfetti rientra anche in una formula. A differenza della differenza dei quadrati perfetti, puoi usare cubi aggiunti, come  , anche facile da trovare con una formula semplice. Questo è quasi esattamente lo stesso di sopra, ma con alcuni vantaggi e svantaggi invertiti. La formula è facile come le altre due e tutto ciò che devi fare è riconoscere i due cubi nel problema:
, anche facile da trovare con una formula semplice. Questo è quasi esattamente lo stesso di sopra, ma con alcuni vantaggi e svantaggi invertiti. La formula è facile come le altre due e tutto ciò che devi fare è riconoscere i due cubi nel problema:
 , anche facile da trovare con una formula semplice. Questo è quasi esattamente lo stesso di sopra, ma con alcuni vantaggi e svantaggi invertiti. La formula è facile come le altre due e tutto ciò che devi fare è riconoscere i due cubi nel problema:
, anche facile da trovare con una formula semplice. Questo è quasi esattamente lo stesso di sopra, ma con alcuni vantaggi e svantaggi invertiti. La formula è facile come le altre due e tutto ciò che devi fare è riconoscere i due cubi nel problema:

![Binomi di factoring {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Binomi di factoring {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)

Consigli
- Non tutti i binomi hanno divisori comuni! Alcuni sono già stati semplificati il più possibile.
- Se non sei sicuro che esista un divisore comune, dividi prima per numeri più piccoli. Ad esempio, se non vedi immediatamente che 16 è il divisore comune di 32 e 16, inizia a dividere entrambi i numeri per 2. Rimangono 16 e 8, che possono anche essere divisi per 8. Ora hai 2 e 1, i fattori più piccoli. C`è chiaramente un divisore comune maggiore di 8 e 2.
- Si noti che una sesta potenza (x) è sia un quadrato perfetto e è un cubo perfetto. Quindi puoi applicare una delle formule speciali sopra, in qualsiasi ordine, a un binomio che è la differenza di seste potenze perfette, come x - 64. Tuttavia, potresti trovare più facile applicare prima la formula della differenza per i quadrati perfetti in modo da poter fattorizzare ulteriormente il binomio.
Avvertenze
- Un binomio che è la somma dei quadrati perfetti non può essere scomposto.
Articoli sull'argomento "Binomi di factoring"
Condividi sui social network:
Popolare