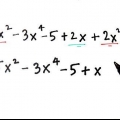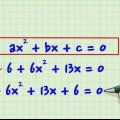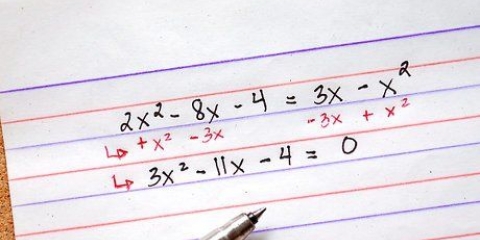In (x + 3x), vediamo che x è uguale. A (-6x - 18), vediamo che -6 è uguale. 
Fattorizzazione x otteniamo x(x + 3). Scomponendo -6 dal secondo pezzo otteniamo -6(x + 3). 
Questo dà (x + 3)(x - 6). 
Le soluzioni sono -3 e √6. 

I fattori sono i numeri che puoi moltiplicare insieme per ottenere un altro numero. In questo caso, questi sono i fattori di 10, o "D": 1, 2, 5 e 10. 
Inizia usando il primo fattore,1. sostituire "1" per ciascuno "X" nel confronto:
(1) - 4(1) - 7(1) + 10 = 0 Questo dà: 1 - 4 - 7 + 10 = 0. Poiché 0 = 0 è un`affermazione vera, sai che x = 1 è la soluzione. 
"x = 1" equivale a "x - 1 = 0" o "(x - 1)". Ne hai solo uno "1" sottratto da ciascun lato dell`equazione. 
Puoi fattorizzare (x - 1) da x? No, non è possibile. Ma se prendi prima in prestito a -x dalla seconda variabile: x(x - 1) = x - x. Puoi calcolare (x - 1) da ciò che rimane della seconda variabile? No, anche questo non è possibile qui. Devi prendere in prestito di nuovo qualcosa dalla terza variabile, che è 3x di -7x. Questo ci dà -3x(x - 1) = -3x + 3x. Dato che hai preso 3x su -7x, la terza variabile è ora -10x e la costante è 10. Puoi sciogliere questo. Sì, naturalmente! -10(x - 1) = -10x + 10. Quello che hai fatto è riorganizzare le variabili in modo da poter ottenere il fattore (x - 1) dall`intera equazione. L`equazione modificata è simile a questa: x - x - 3x + 3x - 10x + 10 = 0, ma è sempre la stessa di x - 4x - 7x + 10 = 0. 
x(x - 1) - 3x(x - 1) - 10(x - 1) = 0. Puoi riorganizzarli per renderli più facili da dissolvere di nuovo: (x - 1)(x - 3x - 10) = 0. Qui stai solo cercando di calcolare (x - 3x - 10). I fattori diventano quindi (x + 2)(x - 5). 
(x - 1)(x + 2)(x - 5) = 0 Questo fornisce le soluzioni per1, -2 e 5. Inserisci -2 nell`equazione: (-2) - 4(-2) - 7(-2) + 10 = -8 - 16 + 14 + 10 = 0. Inserisci 5 nell`equazione: (5) - 4(5) - 7(5) + 10 = 125 - 100 - 35 + 10 = 0.
Fattorizzazione di un polinomio di terzo grado
Contenuto
Questo articolo riguarda la fattorizzazione di un polinomio cubico, chiamato anche polinomio. Esploreremo come possiamo farlo usando il raggruppamento e usando i fattori del termine libero.
Passi
Parte 1 di 2: sciogliere per raggruppamento

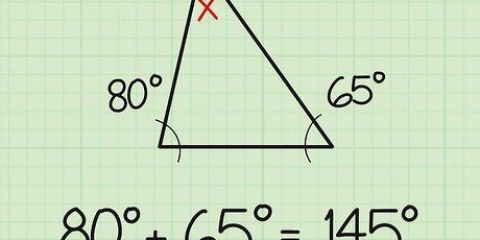
1. Dividi il polinomio in due gruppi. La divisione del polinomio aiuta a risolvere ogni singola parte.
- Supponiamo di lavorare con il seguente polinomio:" x + 3x - 6x - 18 = 0. Dividiamolo in (x + 3x) e (-6x - 18)

2. Prova a scoprire cosa c`è di uguale in ogni gruppo.

3. Rimuovere questi fattori uguali dai due termini.

4. Se ciascuno dei due termini contiene lo stesso fattore, puoi combinare questi fattori.

5. Trova la soluzione osservando le radici. Se hai x in una radice quadrata, ricorda che sia i numeri positivi che quelli negativi sono validi per quell`equazione.
Parte 2 di 2: Factoring con il termine libero

1. Riordina l`espressione nella forma seguente: ax+bx+cx+d.
- Supponiamo di lavorare con l`equazione: x - 4x - 7x + 10 = 0.

2. Trova tutti i fattori di "D". La costante "D" diventa il numero senza variabili accanto ad esso come "X".

3. Trova un fattore che renda il polinomio uguale a zero. Vogliamo determinare quale fattore rende il polinomio uguale a zero se applichiamo questo fattore "X" compilare l`equazione.
(1) - 4(1) - 7(1) + 10 = 0

4. Ora vai a riordinare tutto. Se x=1 allora è possibile scrivere questa equazione in modo leggermente diverso senza cambiarne il significato.

5. Scomponi la radice quadrata dell`equazione. "(x - 1)" è la radice. Prova a tenerne conto dal resto dell`equazione. Fallo con un polinomio alla volta.

6. Procedere alla sostituzione dei fattori del termine libero. Guarda i numeri che hai risolto usando (x - 1) nel passaggio 5:

7. La tua soluzione sono le radici fattorizzate. Verifica questa soluzione inserendo di nuovo ciascuno di essi nell`equazione originale.
Consigli
- L`equazione cubica è il prodotto di 3 equazioni di primo grado o di un`equazione di primo grado e di un`equazione di secondo grado che non possono essere scomposte in fattori. In quest`ultimo caso, dopo aver trovato il polinomio di primo grado, si usa la divisione lunga per trovare il polinomio di secondo grado.
- Non ci sono polinomi cubici che non possono essere fattorizzati quando si tratta di numeri reali, perché questa equazione deve avere una radice quadrata di numeri reali. Equazioni di terzo grado come x + x + 1 che hanno una radice reale irrazionale non possono essere scomposte in polinomi con numeri interi o razionali come coefficiente. Sebbene possa essere preso in considerazione nell`equazione stessa, non può essere ridotto a un polinomio intero.
Il metodo 2 equivale alla divisione lunga di due polinomi, a.v:
(x-1) ∕x³ - 4x²-7x+10 ∕
- x³ - 1x².................................= (x-1) (x²)
- - 3x²-7x
- 3x²+ 3x.........................= (x-1) (-3x)
- - 10x + 10
- 10x + 10................= (x-1) (-10)
- 0............................ x²- 3x-10 (quoziente)
I determina x², -3x e -10 del quoziente si ottengono sottraendo sempre il 1° termine del divisore ( x ) dal primo termine del dividendo, o ciò che ne resta ( x³, -3x², -10x ).
Articoli sull'argomento "Fattorizzazione di un polinomio di terzo grado"
Condividi sui social network:
Popolare