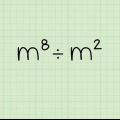Dieci alla potenza di tre











Come mostrato qui, puoi continuare a moltiplicare la base per il prodotto di ciascuna delle prime coppie di numeri fino a ottenere la risposta finale. Continua semplicemente a moltiplicare i primi due numeri, quindi moltiplica questa risposta per il numero successivo nella sequenza. Questo vale per qualsiasi esponente. Quando hai finito con l`esempio, ottieni  .
. 




Usa un motore di ricerca come Startpage, Duckduckgo o Google per trovare la risposta. Puoi utilizzare il pulsante `^` sul tuo computer, tablet o smartphone per inserire l`espressione nella casella di ricerca e vedrai immediatamente la risposta e suggerimenti per espressioni simili da esplorare (Duckduckgo mostra anche una calcolatrice completa). 





Poiché tutto è lo stesso numero, ma moltiplicato, possiamo combinare questi: 




Poiché le basi sono le stesse, puoi semplicemente sommarle insieme: 




Come vedrai tra poco, qualsiasi numero che fa parte di una frazione, ad esempio  , essere riscritto come
, essere riscritto come  . Gli esponenti negativi formano frazioni.
. Gli esponenti negativi formano frazioni. 
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Ricorda che un numero senza potenza ha l`esponente 1
Ricorda che un numero senza potenza ha l`esponente 1 =
= 
 =
= 




![Risolvere gli esponenti x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Risolvere gli esponenti ({sqrt[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)



Risolvere gli esponenti
Contenuto
Gli esponenti vengono utilizzati quando un numero viene moltiplicato per se stesso. Invece di 



Passi
Metodo 1 di 3: risoluzione di esponenti semplici

1. Impara i termini e il vocabolario corretti per problemi esponenziali. Hai un esponente come?  , quindi lavori con due semplici parti. Il numero di telaio qui è un 2, o il base. Questo numero è elevato alla potenza di 3, noto anche come il esponente o potenza. Stiamo parlando
, quindi lavori con due semplici parti. Il numero di telaio qui è un 2, o il base. Questo numero è elevato alla potenza di 3, noto anche come il esponente o potenza. Stiamo parlando  , poi diciamo `due alla terza`, `due alla terza potenza`, o `due eleva alla terza potenza`.`
, poi diciamo `due alla terza`, `due alla terza potenza`, o `due eleva alla terza potenza`.`
 , quindi lavori con due semplici parti. Il numero di telaio qui è un 2, o il base. Questo numero è elevato alla potenza di 3, noto anche come il esponente o potenza. Stiamo parlando
, quindi lavori con due semplici parti. Il numero di telaio qui è un 2, o il base. Questo numero è elevato alla potenza di 3, noto anche come il esponente o potenza. Stiamo parlando  , poi diciamo `due alla terza`, `due alla terza potenza`, o `due eleva alla terza potenza`.`
, poi diciamo `due alla terza`, `due alla terza potenza`, o `due eleva alla terza potenza`.` - Se un numero viene elevato alla seconda potenza, ad esempio
, allora puoi anche dire che il numero lo è quadrato è, come `cinque al quadrato.`
- Se un numero viene elevato alla terza potenza, ad esempio
, allora puoi anche dire quel numero a numero del cubo è.
- Se viene menzionato un numero senza esponente, come ad esempio 4, allora è teoricamente nella prima potenza e può essere riscritto come
.
- Se l`esponente è uguale a 0 e un "numero (diverso da zero)" è elevato a "potenza zero", l`intero è uguale a 1, come
o anche qualcosa di simile
Maggiori informazioni su questo nella sezione "Suggerimenti".

2. Moltiplicare la base per il numero di volte indicato dall`esponente. Se devi risolvere un potere a mano, inizi riscrivendolo come una moltiplicazione. Moltiplichi la base il numero di volte per se stessa, come indicato dall`esponente. Allora, hai tu  poi moltiplichi tre quattro volte per se stesso
poi moltiplichi tre quattro volte per se stesso  . Alcuni altri esempi sono:
. Alcuni altri esempi sono:
 poi moltiplichi tre quattro volte per se stesso
poi moltiplichi tre quattro volte per se stesso  . Alcuni altri esempi sono:
. Alcuni altri esempi sono:



3. Risolvi un`espressione: Moltiplica i primi due numeri per ottenere il prodotto. Ad esempio, con  , inizi con
, inizi con  Sembra un compito noioso, ma fallo passo dopo passo. Inizia moltiplicando i primi due quattro. Quindi sostituisci i due quattro con la risposta come mostrato di seguito:
Sembra un compito noioso, ma fallo passo dopo passo. Inizia moltiplicando i primi due quattro. Quindi sostituisci i due quattro con la risposta come mostrato di seguito:
 , inizi con
, inizi con  Sembra un compito noioso, ma fallo passo dopo passo. Inizia moltiplicando i primi due quattro. Quindi sostituisci i due quattro con la risposta come mostrato di seguito:
Sembra un compito noioso, ma fallo passo dopo passo. Inizia moltiplicando i primi due quattro. Quindi sostituisci i due quattro con la risposta come mostrato di seguito:



4. Moltiplica la risposta della prima coppia (16) per il numero successivo. Continua a moltiplicare i numeri per "crescere" il tuo esponente. Continuando con il nostro esempio, moltiplichiamo 16 per il prossimo 4 in modo che:






 .
.
5. Prova anche i seguenti esempi e controlla le tue risposte con una calcolatrice.




6. Usa `exp,` `X n  ` o `^` della calcolatrice per gli esponenti. È quasi impossibile trovare esponenti più grandi, come
` o `^` della calcolatrice per gli esponenti. È quasi impossibile trovare esponenti più grandi, come  a mano, ma i calcolatori possono gestirlo facilmente. Il pulsante per questo è solitamente indicato in modo abbastanza chiaro. La calcolatrice di Windows può essere espansa in una calcolatrice scientifica facendo clic sulla scheda "Visualizza" della calcolatrice e selezionando "Scientifico". Se desideri ripristinare la calcolatrice predefinita, fai di nuovo clic su "Visualizza" e seleziona "Predefinito".
a mano, ma i calcolatori possono gestirlo facilmente. Il pulsante per questo è solitamente indicato in modo abbastanza chiaro. La calcolatrice di Windows può essere espansa in una calcolatrice scientifica facendo clic sulla scheda "Visualizza" della calcolatrice e selezionando "Scientifico". Se desideri ripristinare la calcolatrice predefinita, fai di nuovo clic su "Visualizza" e seleziona "Predefinito".
 ` o `^` della calcolatrice per gli esponenti. È quasi impossibile trovare esponenti più grandi, come
` o `^` della calcolatrice per gli esponenti. È quasi impossibile trovare esponenti più grandi, come  a mano, ma i calcolatori possono gestirlo facilmente. Il pulsante per questo è solitamente indicato in modo abbastanza chiaro. La calcolatrice di Windows può essere espansa in una calcolatrice scientifica facendo clic sulla scheda "Visualizza" della calcolatrice e selezionando "Scientifico". Se desideri ripristinare la calcolatrice predefinita, fai di nuovo clic su "Visualizza" e seleziona "Predefinito".
a mano, ma i calcolatori possono gestirlo facilmente. Il pulsante per questo è solitamente indicato in modo abbastanza chiaro. La calcolatrice di Windows può essere espansa in una calcolatrice scientifica facendo clic sulla scheda "Visualizza" della calcolatrice e selezionando "Scientifico". Se desideri ripristinare la calcolatrice predefinita, fai di nuovo clic su "Visualizza" e seleziona "Predefinito".Metodo 2 di 3: addizione, sottrazione e moltiplicazione di esponenti

1. Puoi aggiungere o sottrarre numeri di potenza l`uno dall`altro solo se hanno la stessa base e lo stesso esponente. Se hai a che fare con basi ed esponenti identici, come  , quindi puoi semplificare l`addizione dei termini a una moltiplicazione. Non dimenticare quello
, quindi puoi semplificare l`addizione dei termini a una moltiplicazione. Non dimenticare quello  può essere considerato come
può essere considerato come  , così che
, così che  aggiungendo, dove `1 di quello + 1 di quello = 2 di quello`, qualunque `quello` possa essere. Basta sommare il numero di termini simili (quelli con base ed esponente identici) e moltiplicare la somma per quell`espressione esponenziale. Puoi allora
aggiungendo, dove `1 di quello + 1 di quello = 2 di quello`, qualunque `quello` possa essere. Basta sommare il numero di termini simili (quelli con base ed esponente identici) e moltiplicare la somma per quell`espressione esponenziale. Puoi allora  risolvi e moltiplica la risposta per due. Ricorda che questo è possibile perché una moltiplicazione non è altro che riscrivere un`addizione, perché
risolvi e moltiplica la risposta per due. Ricorda che questo è possibile perché una moltiplicazione non è altro che riscrivere un`addizione, perché  . Ecco alcuni esempi:
. Ecco alcuni esempi:
 , quindi puoi semplificare l`addizione dei termini a una moltiplicazione. Non dimenticare quello
, quindi puoi semplificare l`addizione dei termini a una moltiplicazione. Non dimenticare quello  può essere considerato come
può essere considerato come  , così che
, così che  aggiungendo, dove `1 di quello + 1 di quello = 2 di quello`, qualunque `quello` possa essere. Basta sommare il numero di termini simili (quelli con base ed esponente identici) e moltiplicare la somma per quell`espressione esponenziale. Puoi allora
aggiungendo, dove `1 di quello + 1 di quello = 2 di quello`, qualunque `quello` possa essere. Basta sommare il numero di termini simili (quelli con base ed esponente identici) e moltiplicare la somma per quell`espressione esponenziale. Puoi allora  risolvi e moltiplica la risposta per due. Ricorda che questo è possibile perché una moltiplicazione non è altro che riscrivere un`addizione, perché
risolvi e moltiplica la risposta per due. Ricorda che questo è possibile perché una moltiplicazione non è altro che riscrivere un`addizione, perché  . Ecco alcuni esempi:
. Ecco alcuni esempi: 
2. Moltiplica i numeri con la stessa base sommando gli esponenti. Se hai due esponenti con la stessa base, ad esempio  , quindi devi solo sommare i due esponenti con la stessa base. Così,
, quindi devi solo sommare i due esponenti con la stessa base. Così, . Se lo trovi un po` strano, scomponilo in parti più piccole per capire come funziona il sistema:
. Se lo trovi un po` strano, scomponilo in parti più piccole per capire come funziona il sistema:
 , quindi devi solo sommare i due esponenti con la stessa base. Così,
, quindi devi solo sommare i due esponenti con la stessa base. Così, . Se lo trovi un po` strano, scomponilo in parti più piccole per capire come funziona il sistema:
. Se lo trovi un po` strano, scomponilo in parti più piccole per capire come funziona il sistema:






3. Moltiplica un numero esponenziale elevato a un`altra potenza, ad esempio ( X 2 ) 5  . Se aumenti un numero a una certa potenza e il tutto viene elevato a una certa potenza, basta moltiplicare i due esponenti. Così,
. Se aumenti un numero a una certa potenza e il tutto viene elevato a una certa potenza, basta moltiplicare i due esponenti. Così,  . Se ti confondi, ripensa a cosa significano effettivamente questi simboli.
. Se ti confondi, ripensa a cosa significano effettivamente questi simboli.  significa solo te
significa solo te  Moltiplica 5 volte per se stesso, quindi:
Moltiplica 5 volte per se stesso, quindi:
 . Se aumenti un numero a una certa potenza e il tutto viene elevato a una certa potenza, basta moltiplicare i due esponenti. Così,
. Se aumenti un numero a una certa potenza e il tutto viene elevato a una certa potenza, basta moltiplicare i due esponenti. Così,  . Se ti confondi, ripensa a cosa significano effettivamente questi simboli.
. Se ti confondi, ripensa a cosa significano effettivamente questi simboli.  significa solo te
significa solo te  Moltiplica 5 volte per se stesso, quindi:
Moltiplica 5 volte per se stesso, quindi:



4. Pensa agli esponenti negativi come frazioni o al reciproco del numero. Non so cosa sia un reciproco, nessun problema. Se hai a che fare con un esponente negativo, come  , quindi rendi positivo l`esponente e poni questo come denominatore sotto uno, risultando
, quindi rendi positivo l`esponente e poni questo come denominatore sotto uno, risultando  . Ecco alcuni esempi aggiuntivi:
. Ecco alcuni esempi aggiuntivi:
 , quindi rendi positivo l`esponente e poni questo come denominatore sotto uno, risultando
, quindi rendi positivo l`esponente e poni questo come denominatore sotto uno, risultando  . Ecco alcuni esempi aggiuntivi:
. Ecco alcuni esempi aggiuntivi:


5. Dividi due numeri con la stessa base sottraendo gli esponenti. La divisione è l`opposto della moltiplicazione e, sebbene non siano risolti esattamente come opposti, sono qui. Se hai a che fare con l`equazione  , basta sottrarre l`esponente superiore da quello inferiore e lasciare la base così com`è. Così,
, basta sottrarre l`esponente superiore da quello inferiore e lasciare la base così com`è. Così,  , o 16.
, o 16.
 , basta sottrarre l`esponente superiore da quello inferiore e lasciare la base così com`è. Così,
, basta sottrarre l`esponente superiore da quello inferiore e lasciare la base così com`è. Così,  , o 16.
, o 16. , essere riscritto come
, essere riscritto come  . Gli esponenti negativi formano frazioni.
. Gli esponenti negativi formano frazioni.
6. Prova alcuni esercizi pratici per abituarti a lavorare con i numeri di potenza. I seguenti esercizi mettono in pratica tutto quanto discusso finora. Per la risposta, seleziona la riga che contiene il problema.
 = 125
= 125 = 12
= 12 = -x^12
= -x^12 =
=  Ricorda che un numero senza potenza ha l`esponente 1
Ricorda che un numero senza potenza ha l`esponente 1 =
= 
 =
= 
Metodo 3 di 3: Risolvere le frazioni come numeri di potenza

1. Tratta le frazioni sotto forma di numeri di potenza, come X 1 2  come radice quadrata.
come radice quadrata.  in effetti è esattamente lo stesso di
in effetti è esattamente lo stesso di  . Questo è vero indipendentemente dal denominatore della frazione, quindi
. Questo è vero indipendentemente dal denominatore della frazione, quindi  diventa la radice quadratica di x, anche scritta come
diventa la radice quadratica di x, anche scritta come ![Risolvere gli esponenti {sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
.
 come radice quadrata.
come radice quadrata.  in effetti è esattamente lo stesso di
in effetti è esattamente lo stesso di  . Questo è vero indipendentemente dal denominatore della frazione, quindi
. Questo è vero indipendentemente dal denominatore della frazione, quindi  diventa la radice quadratica di x, anche scritta come
diventa la radice quadratica di x, anche scritta come ![Risolvere gli esponenti {sqrt[ {4}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6193130540098748b8aecf0b95bf490c2ae3d867) .
. - Le radici sono l`inverso degli esponenti. Ad esempio, se prendi la risposta di
alla quarta potenza, poi torni a
, e così può
essere anche scritto come
. Un altro esempio è
poi
e quindi
.

2. Rendi il numeratore un esponente normale per una frazione mista. può sembrare impossibile, ma è facile se ricordi come si moltiplicano gli esponenti. Rendi la base una radice quadrata, come una normale frazione, e eleva il tutto alla potenza in cima alla frazione. Se trovi difficile ricordarlo, ripassa la teoria. Alla fine vale
può sembrare impossibile, ma è facile se ricordi come si moltiplicano gli esponenti. Rendi la base una radice quadrata, come una normale frazione, e eleva il tutto alla potenza in cima alla frazione. Se trovi difficile ricordarlo, ripassa la teoria. Alla fine vale  solo uguale
solo uguale  Ad esempio:
Ad esempio:
 può sembrare impossibile, ma è facile se ricordi come si moltiplicano gli esponenti. Rendi la base una radice quadrata, come una normale frazione, e eleva il tutto alla potenza in cima alla frazione. Se trovi difficile ricordarlo, ripassa la teoria. Alla fine vale
può sembrare impossibile, ma è facile se ricordi come si moltiplicano gli esponenti. Rendi la base una radice quadrata, come una normale frazione, e eleva il tutto alla potenza in cima alla frazione. Se trovi difficile ricordarlo, ripassa la teoria. Alla fine vale  solo uguale
solo uguale  Ad esempio:
Ad esempio:

![Risolvere gli esponenti x^{{{frac{1}{3}}}}={sqrt[ {3}]{x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/759eade6ce89e27b301ccdcd83d7e8858827b8e2)
 =
= ![Risolvere gli esponenti ({sqrt[ {3}]{x}})^{5}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea002d6365c3ba2d1d255162136605453a7135f)

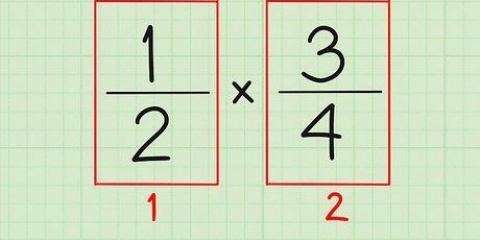
3. Puoi aggiungere, sottrarre e moltiplicare frazioni sotto forma di numeri di potenza, proprio come faresti normalmente. È molto più facile aggiungere o sottrarre gli esponenti prima di risolverli o convertirli in radici quadrate. Se la base è la stessa e l`esponente è lo stesso, puoi semplicemente sommarli e sottrarli. Se solo la base è la stessa, puoi moltiplicare e dividere gli esponenti come al solito, purché tu tenga conto come aggiungere e sottrarre frazioni. Ad esempio:


Consigli
- La maggior parte delle calcolatrici ha un pulsante per gli esponenti - premere dopo aver inserito la base - per risolvere i problemi relativi ai numeri di potenza.Di solito sembra un ^ o x^y.
- `Semplificare` in matematica significa apportare le modifiche necessarie per ottenere la forma più semplice delle espressioni in questione.
- 1 è l`elemento identitario degli esponenti. Ciò significa che qualsiasi numero reale elevato alla potenza di 1 (alla prima potenza) è il numero stesso, ad esempio:
Inoltre, 1 è l`elemento identitario della moltiplicazione (1 come moltiplicatore, ad esempio
), e dalla divisione (1 come dividendo, ad esempio
.
- La base da zero a zero (0) non è definita (inglese: dne, non esiste). I computer o le calcolatrici restituiranno quindi un "errore". Ricorda che qualsiasi numero diverso da zero elevato alla potenza 0 è sempre uguale a 1,
- Ad esempio, la matematica superiore per i numeri immaginari lo è,
, per cui
; e è una costante irrazionale e continua pari a 2,71828..., e a è una costante arbitraria. La dimostrazione può essere trovata nella maggior parte dei libri di matematica superiore.
Avvertenze
- Un aumento esponenziale fa sì che il prodotto salga sempre più velocemente, in modo che la risposta possa apparire sbagliata, quando è corretta. (Verificalo rappresentando graficamente una funzione esponenziale, ad esempio.: 2, se x ha un intervallo di valori diversi).
Articoli sull'argomento "Risolvere gli esponenti"
Condividi sui social network:
Simile
Popolare