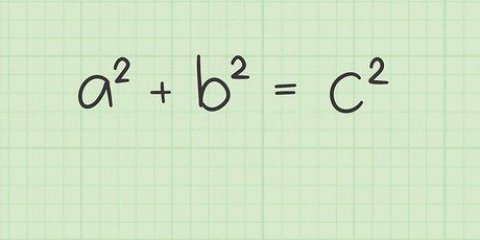Supponiamo di sapere che l`ipotenusa ha una lunghezza di 5 e uno degli altri lati ha una lunghezza di 3. La lunghezza del lato rimanente è sconosciuta. Poiché due dei lati sono noti, possiamo procedere a calcolare la lunghezza del lato sconosciuto! Useremo di nuovo questo esempio più avanti. Se la lunghezza di Due dei lati sono sconosciuti, allora devi determinare la lunghezza di almeno un altro lato per poter usare il teorema di Pitagora. Le funzioni trigonometriche di base possono aiutarti in questo, a condizione che tu conosca uno degli altri angoli non retti del triangolo. 
Nel nostro esempio conosciamo la lunghezza di un lato e quella dell`ipotenusa (3 & 5), quindi scriviamo la nostra equazione in questo modo: 3² + b² = 5² 
Nel nostro esempio, quadramo 3 e 5 per ottenere risp. 9 e 25 ottenere. Possiamo ora riscrivere l`equazione come 9 + b² = 25. 
Nel nostro esempio, l`equazione è ora 9 + b² = 25. essere² sottraiamo 9 da entrambi i membri dell`equazione. Questo ci lascia con b² = 16. 
Nel nostro esempio, b² = 16, l`equazione dopo aver preso le radici quadrate è b = 4. Quindi possiamo dire che la lunghezza del lato sconosciuto del nostro triangolo è uguale a 4. 
Prendiamo un esempio dal mondo reale. Una scala si appoggia a un muro. Il fondo della scala è a 5 metri dal muro. La scala arriva fino a 20 metri misurati dal fondo del muro. Quanto è lunga la scala? "5 metri è la distanza dal muro” e "la scala è alta 20 metri”. Questo dà un`indicazione della lunghezza dei lati del triangolo. Poiché si suppone che il muro e il terreno formino un angolo retto e la scala sia diagonale al muro ad angolo, possiamo considerare questa disposizione come un triangolo rettangolo, i cui lati hanno una lunghezza di a = 5 e b = 20. La lunghezza della scala è l`ipotenusa, la variabile sconosciuta c. Applichiamo qui il teorema di Pitagora: a² + b² = c² (5)² + (20)² = c² 25 + 400 = c² 425 = c² sqrt(425) = c c = 20,6 . La lunghezza della scala è (approssimativa) 20,6 metri. 


Supponiamo di avere i punti (6.1) e (3.5). La lunghezza del lato orizzontale del nostro triangolo è: |x1 - X2| |3 - 6| | -3 | = 3 La lunghezza del lato verticale è: |y1 - y2| |1 - 5| | -4 | = 4 Quindi possiamo dire che la lunghezza dei lati del nostro triangolo rettangolo è uguale a a = 3 e b = 4. 
Nel nostro esempio, conosciamo i punti (3,5) e (6.1), e le lunghezze dei lati sono a= 3 e b=4, quindi determiniamo l`ipotenusa come segue: sqrt(x) significa "la radice quadrata di x". Non dimenticare di controllare sempre le tue risposte. Se sembra che una risposta non sia corretta, controlla i tuoi calcoli o ricomincia da capo. Se conosci solo un lato del triangolo, ma anche uno degli altri angoli (rispetto all`angolo retto), calcola prima un altro lato usando ciò che sai sulla trigonometria (peccato, cos, abbronzatura) o le proporzioni 30-60- 90 / 45-45-90. Un altro controllo: il lato più lungo si oppone all`angolo più grande e il lato più corto si oppone all`angolo più piccolo.
Usando il teorema di pitagora
Contenuto
Il teorema di Pitagora descrive la lunghezza dei lati di un triangolo rettangolo in un modo così elegante e pratico da essere ancora ampiamente utilizzato oggi. Questo afferma che per ogni triangolo rettangolo, la somma dei quadrati dei lati retti è uguale al quadrato dell`ipotenusa. In altre parole, per un triangolo rettangolo (un triangolo con i lati perpendicolari tra loro), con i lati di lunghezza aeb e un`ipotenusa di lunghezza c: a + b = c. Il teorema di Pitagora è uno dei pilastri della geometria e ha numerose applicazioni pratiche – ad esempio, utilizzando questo teorema è molto facile trovare la distanza tra due punti su un piano piatto.
Passi
Metodo 1 di 2: La lunghezza dei lati di un triangolo rettangolo

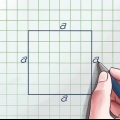
1. Controlla se hai a che fare con un triangolo rettangolo. Il Teorema di Pitagora può essere utilizzato solo per i triangoli rettangoli, quindi prima di procedere, è importante stabilire che il tuo triangolo soddisfi la definizione di triangolo rettangolo. Fortunatamente, qui c`è solo un fattore decisivo: uno degli angoli del triangolo deve essere un angolo di 90 gradi.
- Un indizio è che gli angoli retti sono spesso contrassegnati da una piccola parentesi quadra per indicare che si tratta di un angolo di 90 gradi. Vedi se c`è una parentesi del genere in uno degli angoli del tuo triangolo.

2. Assegna le variabili a, b e c ai lati del triangolo. Nel teorema di Pitagora, le variabili a e b si riferiscono ai lati retti del triangolo e la variabile c all`ipotenusa, il lato lungo opposto all`angolo retto. Quindi per iniziare assegna le variabili aeb (l`ordine non ha importanza) ai lati diritti e assegni c all`ipotenusa.

3. Determina quale lato del triangolo vuoi conoscere. Il teorema di Pitagora permette di trovare la lunghezza di qualsiasi lato di un triangolo, a patto che due dei lati siano noti. Determina quale dei lati ha una lunghezza sconosciuta--un, B, e/oC. Se solo uno è sconosciuto, puoi andare avanti.

4. Calcola usando l`equazione e le note. Inserisci i valori per le lunghezze dei lati del tuo triangolo nell`equazione a + b = c. Ricorda che aeb sono i lati diritti e c è l`ipotenusa.

5. Calcola i quadrati. Per risolvere la tua equazione, inizia quadrando ciascuno dei lati conosciuti. Se lo trovi più facile, puoi lasciare il potere e quadrarlo più tardi.

6. Isolare la variabile sconosciuta su un lato del segno di uguale. Facoltativamente, usa le operazioni algebriche standard per portare l`ignoto su un lato del segno di uguale e i quadrati sull`altro lato. Se stai cercando di trovare l`ipotenusa, allora c è già nella posizione su un lato, quindi puoi saltare quel passaggio.

7. Prendi la radice quadrata di entrambi i membri dell`equazione. Ora dovresti avere un quadrato (variabile) su un lato dell`equazione e un numero sull`altro lato. Ora sottrai la radice quadrata di entrambi i lati per trovare la lunghezza dell`incognita.

8. Usa in pratica il teorema di Pitagora. Il motivo per cui il teorema di Pitagora è usato così tanto è perché è applicabile alla risoluzione di molti problemi pratici. Impara a riconoscere i triangoli rettangoli nel mondo intorno a te: ovunque tu possa identificare un triangolo rettangolo con uno o più oggetti, il teorema di Pitagora può essere utilizzato per trovare la lunghezza di uno dei lati, a condizione che ci siano due lati o che gli angoli siano famosi.
Metodo 2 di 2: Calcola la distanza tra due punti nel piano

1. Definisci due punti nel piano. Il teorema di Pitagora può essere usato molto facilmente per determinare la distanza in linea retta tra due punti del piano. Tutto ciò che serve sono le coordinate xey di due punti qualsiasi. Di solito queste coordinate sono scritte come (x, y).
- Per trovare la distanza tra questi due punti, consideriamo ciascuno dei punti come uno dei vertici di un triangolo rettangolo, che non appartiene all`angolo retto. Questo rende molto facile trovare la lunghezza di aeb, dopodiché si può calcolare c (l`ipotenusa e la distanza tra i due punti).

2. Traccia i due punti su un grafico. In un piano X-Y, per ogni punto (x, y), x è un punto sull`asse x orizzontale e y è un punto sull`asse y verticale. Puoi trovare la distanza tra i due senza rappresentarli graficamente, ma così facendo otterrai un riferimento visivo per verificare se la tua risposta ha senso.

3. Trova la lunghezza dei lati dritti del tuo triangolo. Considerando i tuoi due punti come gli angoli del triangolo adiacenti all`ipotenusa, puoi trovare le lunghezze dei lati a e b. Puoi farlo usando il grafico o usando le formule |x1 - X2| per il lato orizzontale e |y1 - y2| per il lato verticale, dove (x1,y1) è il primo punto e (x2,y2) il secondo punto.

4. Usa il teorema di Pitagora per trovare l`ipotenusa. La distanza tra i due punti è la lunghezza dell`ipotenusa del triangolo. Usa il teorema di Pitagora per trovare l`ipotenusa del triangolo, con lati a, b e c.
- (3)²+(4)²= c²
- c= quadrato(9+16)
- c= sqrt(25)
- c= 5. La distanza tra (3.5) e (6.1) è 5.
Consigli
- Se il triangolo non è un triangolo rettangolo, non puoi semplicemente usare il teorema di Pitagora.
- L`ipotenusa è sempre:
- la linea opposta all`angolo retto
- il lato più lungo del triangolo rettangolo
- la variabile C nel teorema di Pitagora
Articoli sull'argomento "Usando il teorema di pitagora"
Condividi sui social network:
Popolare