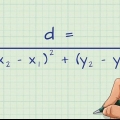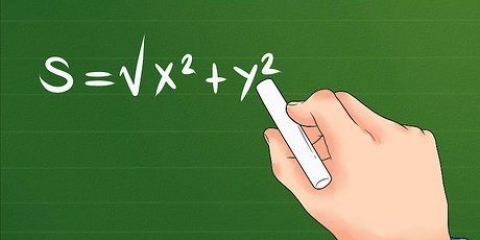Come Calcolare la Distanza Tra Due Punti: 6 Passaggi (con Immagini)

Contenuto

Passi
Consigli

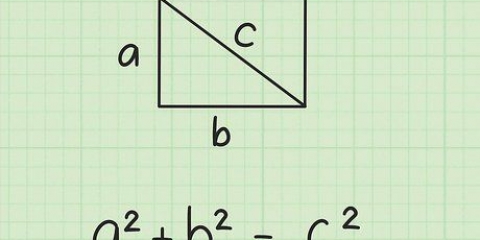
Pensa alla distanza tra due punti qualsiasi come una linea. La lunghezza di questa linea può essere trovata usando la formula della distanza: $\sqrt{(} (X_{2} - X_{1})^{2} + (y_{2} - y_{1})^{2})$ ${sqrt(}(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2})$ .

Passi

Immagine titolata Trova la distanza tra due punti Passaggio 2

1. Prendi le coordinate di due punti tra i quali vuoi trovare la distanza. Chiama un punto 1 (x1,y1) e l`altro punto 2 (x2,y2). Non importa da quale punto inizi, purché applichi le etichette (1 e 2) in modo coerente durante tutto il problema.

x1 è la coordinata orizzontale (lungo l`asse x) del punto 1 e x2 è la coordinata orizzontale del punto 2. y1 è la coordinata verticale (lungo l`asse y) del punto 1 e y2 è la coordinata verticale del punto 2.
No, ad esempio i punti (3.2) e (7.8). Se (3.2) è uguale a (x1,y1), allora (7.8) è uguale a (x2,y2).

Immagine titolata Trova la distanza tra due punti Passaggio 1

2. Usa la formula della distanza. Questa formula determina la lunghezza di una retta tra due punti: il punto 1 e il punto 2. La distanza lineare è la radice quadrata del quadrato della distanza orizzontale, più il quadrato della distanza verticale tra due punti. In poche parole, è la radice quadrata di:

(X 2 - X_{1})^{2} + (y_{2} - y_{1})^{2}

$(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}$

Immagine titolata Trova la distanza tra due punti Passaggio 3

3. Determina la distanza orizzontale e verticale tra i punti. Per prima cosa calcola y2 - y1 per trovare la distanza verticale. Quindi calcola x2 - x1 per trovare la distanza orizzontale. Non preoccuparti se la sottrazione produce numeri negativi. Il passaggio successivo è quadrare questi valori (che si traduce sempre in un numero intero positivo).

Determina la distanza lungo l`asse y. Per l`esempio punti (3.2) e (7.8), dove il punto 1 è (3.2) e il punto 2 (7.8) questo diventa: (y2 - y1) = 8 - 2 = 6. Ciò significa che la distanza sull`asse y tra questi due punti è di sei unità di lunghezza.

Determina la distanza lungo l`asse x. Per gli stessi punti di campionamento (3.2) e (7.8): (x2 - x1) = 7 - 3 = 4. Ciò significa che ci sono quattro unità di lunghezza che separano i due punti sull`asse x.

Immagine titolata Trova la distanza tra due punti Passaggio 4

4. Al quadrato entrambi i valori. Ciò significa che al quadrato la distanza dell`asse x (x2 - x1) e al quadrato la distanza dell`asse y (y2 - y1).

62 = 36

$6^{2}=36$

42 = 16

$4^{2}=16$

Immagine titolata Trova la distanza tra due punti Passaggio 5

5. Unite i quadrati. Questo ti darà il quadrato della distanza lineare diagonale tra i tuoi due punti. Nell`esempio dei punti (3.2) e (7.8) il quadrato di (7 - 3) è 16 e il quadrato di (8 - 2) è 36. 36 + 16 = 52.

Immagine titolata Trova la distanza tra due punti Passaggio 6

6. Prendi la radice quadrata dell`equazione. Questo è l`ultimo passaggio dell`equazione. La distanza lineare tra i due punti è la radice quadrata della somma dei quadrati della distanza sull`asse x e della distanza sull`asse y.

Continuando con l`esempio, la distanza tra (3.2) e (7.8) è la radice quadrata di 52, ovvero circa 7,21.

Consigli

Non importa se ottieni un numero negativo dopo aver sottratto y2 - y1 o x2 - x1. Poiché la differenza è al quadrato, ottieni sempre una distanza positiva nella tua risposta.