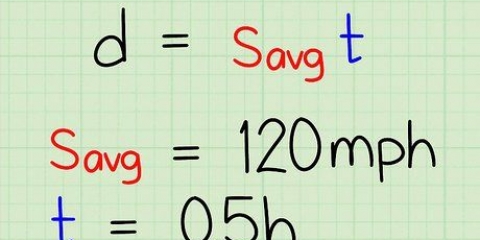Inoltre, non dimenticare di collegare il punto iniziale con il punto finale, utilizzando una linea retta.Questo è lo spostamento che calcoleremo. Ad esempio, se un oggetto percorre prima 300 metri in direzione est e poi 400 metri in direzione nord, si forma un triangolo rettangolo. AB è il primo lato e BC è il secondo lato del triangolo.AC è l`ipotenusa del triangolo e il suo valore è lo spostamento dell`oggetto. In questo esempio, le due direzioni sono "est" e "nord." 
Ad esempio, x = 300 e y = 400.La tua equazione ora appare così: s = √300² + 400². 
Ad esempio: s = √90000 + 160000.s = √250000.s = 500.Ora sai che lo spostamento è pari a 500 metri. 

L`equazione sarà simile a questa: s = 1/2(20 + 23)45. 
Per questa equazione, non importa molto se si scambiano accidentalmente le velocità iniziale e finale. Poiché prima aggiungi questi valori insieme, non importa. Ma in altre equazioni, lo scambio delle velocità iniziale e finale può influenzare la risposta finale o il valore dello spostamento. La tua equazione ora appare così: s = 1/2(43)45.Per prima cosa dividi 43 per 2, che dà 21,5 come risposta. Moltiplica 21,5 per 45, ottenendo 967,5 metri come risposta.967,5 è la cilindrata della vettura, vista dal punto di partenza. 

Sulla base dell`esempio sopra, la tua equazione dovrebbe ora assomigliare a questa: s = 25(4) + 1/2(3)4².Può sicuramente aiutare se metti parentesi attorno ai valori di accelerazione e tempo per mantenere i numeri separati l`uno dall`altro. 
Diamo un`occhiata più da vicino all`equazione: s = 25(4) + 1/2(3)4². L`ordine è: 4² = 16; quindi 16 x 3 = 48; quindi 25 x 4 = 100; e se ultimo 48/2 = 24. L`equazione ora appare così: s = 100 + 24.Dopo l`aggiunta, questo dà s = 124, quindi lo spostamento è di 124 metri. 

Un esempio di incarico: una ragazza è seduta su una giostra. Il suo sedile è a una distanza di 1 metro dal centro del cerchio (il raggio). Se la ragazza si muove lungo un arco circolare di 1,5 metri (spostamento lineare), qual è il suo spostamento angolare? L`equazione si presenta così: θ = 1,5/1. 
Dopo la divisione 1.5/1 ti resta 1.5.Lo spostamento angolare della ragazza è 1,5 radianti. Poiché lo spostamento angolare indica di quanto un oggetto è stato ruotato dalla sua posizione iniziale, è necessario rappresentarlo in radianti, non come distanza. I radianti sono unità utilizzate per misurare gli angoli. 

Lo spostamento è anche chiamato a "quantità vettoriale" indicato come il cambiamento nella posizione di un oggetto rispetto alla direzione in cui l`oggetto si muove. Supponiamo di camminare per 5 metri verso est. Se cammini di nuovo per 5 metri a ovest, ti sposterai nella direzione opposta, tornando al punto di partenza. Anche se hai percorso in totale 10 metri, la tua posizione non è cambiata e il tuo spostamento è quindi di 0 metri. 
Immagina un allenatore di calcio che rimbalza avanti e indietro lungo le linee laterali.Mentre dava indicazioni ai giocatori, ha camminato lungo la linea diverse volte, avanti e indietro. Se tenessi costantemente d`occhio l`allenatore, vedresti la distanza che percorre. Ma supponiamo che l`allenatore si fermi per dire qualcosa a un difensore? Se si trova in un luogo diverso dal suo punto di partenza, allora guardi il movimento dell`allenatore (a un certo momento). 
Un percorso curvo alla fine ti condurrà dal punto iniziale al punto finale, ma questo non è il modo più breve. Per aiutarti a visualizzarlo, immagina di camminare in linea retta e di essere fermato da un pilastro o da un altro ostacolo. Non puoi attraversare il pilastro, quindi giraci intorno. Anche se finisci nello stesso punto come se fossi passato direttamente attraverso il pilastro, devi comunque fare un viaggio più lungo per arrivarci. Sebbene lo spostamento sia preferibilmente in linea retta, è possibile misurare lo spostamento di un oggetto che "bene" si muove lungo un sentiero tortuoso. Questo è chiamato il "spostamento angolare" e può essere calcolato trovando la distanza più breve che esiste tra il punto iniziale e il punto finale. 
Ad esempio, supponiamo di camminare 5 metri a est e poi 3 metri a ovest. Anche se tecnicamente sei a 2 metri dal tuo punto di partenza, lo spostamento è -2 perché in quel punto ti stai muovendo nella direzione opposta.La distanza sarà sempre positiva, perché non conosci una distanza che hai percorso "annullato" può fare. Lo spostamento negativo non significa lo spostamento diminuisce. È semplicemente un modo per indicare che il movimento è nella direzione opposta. 
Quindi questo è possibile solo se ti muovi in linea retta dal punto di partenza e senza cambiare direzione in seguito.Ad esempio, supponiamo che tu viva a San Francisco, in California, e trovi un lavoro a Las Vegas, in Nevada. Dovrai quindi trasferirti a Las Vegas per vivere più vicino al tuo lavoro. Se prendi l`aereo, un volo diretto da San Francisco a Las Vegas, hai percorso 670 km e il tuo spostamento è quindi 670 km. Tuttavia, se viaggi in auto da San Francisco a Las Vegas, la tua distanza potrebbe essere ancora 670 km ma nel frattempo hai percorso 906 km.Poiché la guida di solito comporta un cambio di direzione (spegnere, prendere un percorso diverso), hai percorso una distanza molto maggiore rispetto alla distanza più breve tra le due città.
Calcola spostamento
Contenuto
Il termine spostamento in fisica si riferisce al cambiamento piuttosto che a un oggetto. Quando si calcola lo spostamento, si misura quanto si è spostato un oggetto, in base ai dati dalla posizione iniziale e dalla posizione finale. La formula utilizzata per determinare lo spostamento dipende dalle variabili fornite per un problema. Segui i passaggi seguenti per imparare a calcolare lo spostamento di un oggetto.
Passi
Parte 1 di 5: Calcolo dello spostamento risultante

1. Utilizzare la formula per lo spostamento risultante utilizzando l`unità di lunghezza utilizzata per specificare la posizione iniziale e finale. Sebbene la distanza sia diversa dallo spostamento, una dichiarazione sullo spostamento risultante indicherà di quanto "metro" ha scartato un oggetto. Usa queste unità di misura per calcolare lo spostamento, la distanza di un oggetto dalla sua posizione originale.
- L`equazione per lo spostamento risultante è: s = √x²+y²."S" sta per spostamento.X è la prima direzione in cui si muove l`oggetto e y è la seconda direzione in cui si muove l`oggetto. Se il tuo oggetto si muove solo in 1 direzione, allora y = 0.
- Un oggetto può muoversi solo in un massimo di 2 direzioni, perché muoversi lungo la linea nord-sud o la linea est-ovest è considerato neutro.

2. Collega i punti in base all`ordine di movimento ed etichetta questi punti dalla A alla Z.Usa un righello per disegnare linee rette da un punto all`altro.

3. Immettere i valori per x² e y².Ora che conosci la direzione in cui si sta muovendo il tuo oggetto, puoi iniziare a compilare i valori per le variabili rilevanti.

4. Risolvi l`equazione. Calcolare prima 300² e poi 400², sommarli e sottrarre la radice quadrata della somma.
Parte 2 di 5: Conoscere il vettore di velocità e la durata del tempo

1. Utilizzare questa formula se il problema fornisce il vettore velocità e la durata nel tempo. Può succedere che un problema di fisica non dica una parola sulla distanza percorsa, ma indichi da quanto tempo ha viaggiato un oggetto e a quale velocità. È quindi possibile calcolare lo spostamento utilizzando la durata del tempo e la velocità.
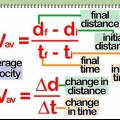
- In questo caso, l`equazione sarà simile a questa: s = 1/2(u + v)t.u = la velocità iniziale dell`oggetto, la velocità alla quale l`oggetto ha iniziato a muoversi in una particolare direzione.v = la velocità finale dell`oggetto, o quanto velocemente è andato alla fine. t = il tempo impiegato dall`oggetto per raggiungere la sua destinazione.
- Ad esempio: un`auto guida per 45 secondi.L`auto ha svoltato ad ovest con una velocità di 20 m/s (velocità iniziale) e alla fine della strada la velocità è di 23 m/s (velocità finale). Calcolato lo spostamento sulla base di questi dati.

2. Immettere i valori per la velocità e il tempo. Ora che sai da quanto tempo sta guidando l`auto e qual è stata la velocità iniziale e finale, puoi trovare la distanza dal punto iniziale al punto finale.

3. Risolvi l`equazione dopo aver inserito i valori. Ricordarsi di calcolare i termini nell`ordine corretto altrimenti lo spostamento andrà storto.
Parte 3 di 5: Quando sono dati velocità, accelerazione e tempo

1. Un`altra equazione è necessaria se per un problema viene data l`accelerazione, insieme alla velocità e al tempo. Con un compito del genere sai qual è stata la velocità iniziale dell`oggetto, qual è l`accelerazione e da quanto tempo l`oggetto è stato sulla strada. Hai bisogno della seguente equazione.
- L`equazione per questo tipo di problema è la seguente: s = ut + 1/2at².Il "voi" rappresenta ancora la velocità iniziale; Il "un" è l`accelerazione dell`oggetto o anche la velocità con cui cambia la velocità dell`oggetto. La variabile"T" può significare il tempo totale o può indicare un periodo specifico in cui l`oggetto ha accelerato. In ogni caso, questo è indicato in unità di tempo come secondi, ore, ecc.
- Supponiamo che un`auto con una velocità iniziale di 25 m/s guadagni un`accelerazione di 3 m/s2 per un periodo di 4 secondi.Qual è la cilindrata dell`auto dopo 4 secondi?

2. Inserisci i valori nella posizione corretta nell`equazione. A differenza dell`equazione precedente, qui viene mostrata solo la velocità iniziale, quindi assicurati di inserire i valori corretti.

3. Calcola lo spostamento risolvendo l`equazione. Un modo rapido per aiutarti a ricordare l`ordine delle operazioni in un`equazione è il mnemonico "Mr. Dale in attesa di risposta".Indica tutte le operazioni aritmetiche nell`ordine corretto (esagerazione, moltiplicazione, divisione, rooting, addizione e sottrazione).
Parte 4 di 5: Calcolo dello spostamento angolare

1. Determinazione dello spostamento angolare quando un oggetto si muove lungo una curva. Sebbene ciò comporti ancora il calcolo dello spostamento utilizzando una linea retta, è necessaria la differenza tra la posizione iniziale e finale lungo un percorso curvo.
- Prendi come esempio una ragazza che è su una giostra. Mentre gira intorno all`esterno della ruota, si muove in cerchio. Lo spostamento angolare cerca di trovare la distanza più breve tra la posizione iniziale e finale se un oggetto non si muove in linea retta.
- La formula per lo spostamento angolare è: θ = S/r, per cui "S" sta per lo spostamento lineare, "R" per il raggio, e "θ" lo spostamento angolare è.Lo spostamento lineare è la distanza percorsa da un oggetto lungo un cerchio.Il raggio è la distanza di un oggetto dal centro del cerchio.Lo spostamento angolare è il valore che vogliamo conoscere.

2. Inserisci i valori dello spostamento lineare e del raggio nell`equazione. Ricorda che il raggio è la distanza dal centro di un cerchio al bordo; può darsi che il diametro sia dato per un problema, nel qual caso dovrai dividerlo per 2 per trovare il raggio (raggio) del cerchio.

3. Dividere lo spostamento lineare per il raggio.Questo ti darà lo spostamento angolare dell`oggetto.
Parte 5 di 5: Capire lo spostamento

1. È importante capirlo "distanza" a volte significa qualcos`altro di "Dislocamento."La distanza dice qualcosa su quanto un oggetto si è spostato in totale.
- La distanza è qualcosa che chiamiamo anche a "scalare" menzionare. È un modo per indicare quanta distanza hai percorso, ma non dice nulla sulla direzione in cui ti sei spostato.
- Ad esempio, se cammini per 2 metri a est, 2 metri a sud, 2 metri a ovest e di nuovo 2 metri a nord, sei di nuovo al punto di partenza. Sebbene tu abbia percorso una distanza totale di 10 metri, il tuo spostamento è pari a 0 metri, perché il tuo punto finale è uguale al tuo punto di partenza.

2. Lo spostamento è la differenza tra due punti. Lo spostamento non è una somma di movimenti come nel caso della distanza; riguarda solo la parte tra il tuo punto di inizio e il tuo punto finale.

3. Ricorda bene le parole "avanti e indietro" quando provi a immaginare uno spostamento. La direzione opposta annulla il movimento nella direzione originale.

4. Lo spostamento è misurato lungo una linea retta, non lungo una traiettoria circolare. Per scoprire il movimento, cerchi il percorso più breve tra due punti diversi.

5. Si prega di comprendere che lo spostamento può anche avere un valore negativo, a differenza della distanza. Se il punto finale viene raggiunto muovendosi in una direzione opposta a quella in cui hai iniziato (rispetto al punto iniziale), il tuo spostamento è negativo.

6. Renditi conto che i valori di distanza e spostamento a volte possono essere gli stessi. Se cammini dritto per 25 metri e poi ti fermi, la distanza che hai percorso è uguale allo spostamento, semplicemente perché non hai cambiato direzione.
Consigli
- Lavora con precisione
- Non memorizzare le formule, ma cerca di capire come funzionano
Necessità
- Calcolatrice
- Misuratore di distanza
Articoli sull'argomento "Calcola spostamento"
Condividi sui social network:
Popolare