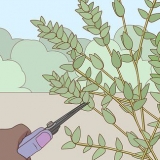
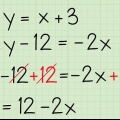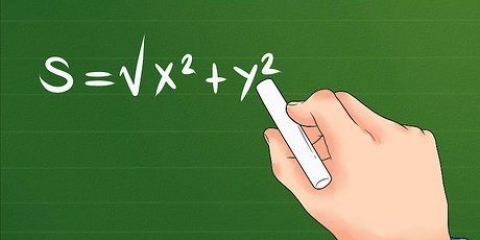Centro dell`altalena=4 metri dal punto zero. Bambino a 1=1 metro di distanza dal punto zero Bambino a 2=5 metri di distanza dal punto zero 



430 m*kg ÷ 130 chilo=3,31 m Il centro di gravità è a 3,31 metri dal punto zero, o misurato dal punto zero è a 3,31 metri dall`estremità del lato sinistro dell`altalena dove è stato posizionato il punto zero. 



Il modo in cui l`abbiamo risolto, lo zero è sul lato sinistro dell`altalena. La nostra risposta è 3,31 m, quindi il nostro centro di massa è 3,31 m dallo zero a sinistra. Se scegli un nuovo punto zero, a 1 m da sinistra, ottieni come risposta 2,31 m dal baricentro. Il baricentro è 2,31 m dal nuovo punto zero, cioè 1 m da sinistra. Il centro di massa è 2,31 + 1=3,31 m da sinistra, e quindi la stessa risposta che abbiamo calcolato prima. (Nota: quando si misura la distanza, ricordare che le distanze sinistra dal punto zero sono negativi e le distanze Giusto di esso positivo.) 
Nei problemi di altalena, tutto ciò che conta è dove il baricentro si trova da sinistra a destra lungo la linea dell`altalena. In seguito potresti imparare metodi più avanzati per calcolare il centro di gravità in due dimensioni.
Calcola il baricentro
Contenuto
Il centro di gravità (il centro di massa) è il centro della distribuzione del peso di un oggetto, il punto in cui la gravità agisce su quell`oggetto. Questo è il punto in cui l`oggetto è in perfetto equilibrio, indipendentemente da come l`oggetto viene ruotato o ruotato attorno a quel punto. Se vuoi sapere come calcolare il baricentro di un oggetto, hai bisogno del peso dell`oggetto e di tutti gli oggetti su di esso. Quindi determini uno zero ed elabori le quantità note nell`equazione, per calcolare il baricentro di un oggetto o di un sistema. Se vuoi sapere come calcolare il baricentro, segui i passaggi seguenti.
Passi
Metodo 1 di 4: Determina il peso

1. Calcola il peso dell`oggetto. Quando calcoli il baricentro, dovrai prima scoprire il peso dell`oggetto. Diciamo che vuoi calcolare il peso di un`altalena con una massa di 30 chili. Poiché è un oggetto simmetrico, il suo centro di gravità sarà esattamente nel mezzo (se nessuno è seduto su di esso). Ma se ci sono persone con masse diverse sull`altalena, allora il problema si complica un po`.

2. Calcola i pesi extra. Per determinare il baricentro dell`altalena con due bambini su di essa, dovrai determinare il peso individuale di ogni bambino. Il primo figlio ha una massa di 40 chili e il secondo figlio di 60 chili.
Metodo 2 di 4: Determina il punto zero

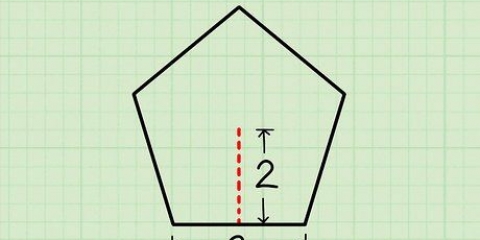
1. Scegli un punto zero. Il punto zero è qualsiasi punto di partenza su un lato dell`altalena. Puoi posizionare lo zero su un lato dell`altalena o sull`altro lato. Diciamo che l`altalena è lunga 6 metri. Mettiamo lo zero sul lato sinistro dell`altalena, vicino al primo figlio.

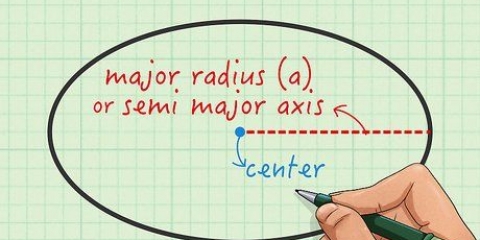
2. Misurare la distanza dal punto zero al centro dell`oggetto principale e ai due pesi aggiuntivi. Diciamo che i bambini sono ciascuno a 1 metro da ciascuna estremità dell`altalena. Il centro dell`altalena è il centro dell`altalena, ovvero 3 metri, perché 6 metri divisi per 2 equivalgono a 3. Ecco le distanze dal centro dell`oggetto più grande e i due pesi aggiuntivi formano il punto zero:
Metodo 3 di 4: Determina il baricentro

1. Moltiplica la distanza di ogni oggetto al punto zero per il suo peso per trovare il momento. Questo ti dà il momento per ogni oggetto. Ecco come moltiplicare la distanza di ogni oggetto dal punto zero per il suo peso:
- L`altalena: 30 kg x 3 m=90 m*kg.
- Bambino 1=40 kg x 1 m=40 m*kg.
- Bambino 2=60 kg x 5 m=300 m*kg.

2. Somma i tre momenti insieme. Basta calcolare quanto segue: 90 m*kg + 40 m*kg + 300 m*kg=430 m*kg. Il momento totale è di 430 m*kg.

3. Somma i pesi di tutti gli oggetti insieme. Trova la somma dei pesi dell`altalena e dei due bambini. Procedi come segue: 30 chili + 40 chili + 60 chili = 130 chili.

4. Dividi il momento totale per il peso totale. Ottiene la distanza dal punto zero al centro di gravità dell`oggetto. Questo dividendo 430 m * kg per 130 chili.
Metodo 4 di 4: controlla la tua risposta

1. Trova il baricentro nel diagramma. Se il centro di gravità che hai trovato è al di fuori del sistema di oggetti, allora hai trovato la risposta sbagliata. Forse hai calcolato la distanza da più di un punto. Riprova con un solo punto zero.
- Ad esempio, per le persone sedute sull`altalena, il baricentro dovrebbe trovarsi da qualche parte sull`altalena, non a sinistra oa destra dell`altalena. Non deve essere su una persona.
- Questo vale anche per problemi a due dimensioni. Disegna un quadrato abbastanza grande da contenere tutti gli oggetti del tuo problema. Il baricentro deve trovarsi all`interno di questo quadrato.

2. Controlla i tuoi calcoli se la tua risposta è troppo piccola. Se hai scelto un`estremità del sistema come zero, una piccola risposta posiziona il baricentro proprio accanto a un`estremità. Questa potrebbe essere la risposta corretta, ma spesso è un`indicazione che qualcosa è andato storto. Hai il peso e la distanza tra loro nel calcolo moltiplicato? Questo è il modo giusto per trovare questo momento. Se accidentalmente sommati, quindi probabilmente otterrai una risposta molto più piccola.

3. Controlla il tuo calcolo se hai trovato più di un baricentro. Ogni sistema ha un solo baricentro. Se ce ne sono di più, potresti aver saltato il passaggio in cui dovevi sommare tutti i momenti. Il centro di gravità è quello totale momento diviso per il totale peso. Tu non devi ogni momento di condivisione ogni peso, che ti dà solo la posizione di ogni oggetto.

4. Controlla lo zero se la tua risposta è un intero fuori. La risposta nel nostro esempio è 3,31 m Supponiamo che ti siano stati dati 2,31 m, 4,31 m o qualche altro numero che termina con `.31.Ciò è probabilmente dovuto al fatto che abbiamo scelto l`estremità sinistra dell`altalena come zero, mentre tu hai scelto l`estremità destra o un altro punto a una distanza intera dal nostro zero. La tua risposta è corretta, indipendentemente dallo zero che scegli! Devi solo ricordarlo lo zero sta sempre per x=0. Ecco un esempio:

5. Assicurati che tutte le tue misure siano linee rette. Supponiamo di vedere un altro esempio con "bambini su un`altalena", ma un bambino è molto più grande dell`altro, o un ragazzo è appeso sotto l`altalena, invece di sederci sopra. Ignora la differenza e prendi tutte le misure lungo la linea retta dell`altalena. Misurare le distanze ad angolo produrrà risposte vicine, ma leggermente diverse.
Consigli
- Per determinare la distanza che una persona deve percorrere per bilanciare l`altalena sul supporto, utilizzare questa formula: (sposta il peso) / (peso totale)=(distanza oltre la quale si è spostato il baricentro) / (distanza oltre la quale il peso è stato spostato). Questa formula può essere riscritta per mostrare che la distanza che il peso (la persona) deve spostare è uguale alla distanza tra il baricentro e il fulcro, moltiplicata per il peso della persona diviso per il peso totale. Così deve il primo figlio -1,31 m *40 chilo / 130 chilo=-0.sposta 40 m (fino alla fine dell`altalena). O dovrebbe il secondo figlio -1.08 m *130 chilo / 60 chilo=-2.sposta 84 m. (al centro dell`altalena).
- Per trovare il baricentro di un oggetto bidimensionale, usa la formula Xcg=∑xW/∑W per trovare il baricentro lungo l`asse x e Ycg=∑yW/∑W per trovare il baricentro lungo l`asse y per trovare. Il punto in cui si intersecano è il baricentro.
- La definizione del baricentro di una distribuzione di massa generale è (∫ r dW/∫ dW) dove dW è uguale alla derivata del peso, r è il vettore di posizione, e dove gli integrali sono da interpretare come integrali di Stieltjes sull`intero corpo. Tuttavia, possono essere espressi come integrali di volume di Riemann o Lebesgue più convenzionali per distribuzioni con una funzione di densità di probabilità. A partire da questa definizione, tutte le proprietà del baricentro, comprese quelle utilizzate in questo articolo, possono essere derivate dalle proprietà degli integrali di Stieltjes.
Avvertenze
- Non tentare ciecamente di applicare questi meccanismi senza comprendere la teoria, che può portare a errori. Per prima cosa cerca di capire le leggi/teorie sottostanti.
Articoli sull'argomento "Calcola il baricentro"
Condividi sui social network:
Popolare