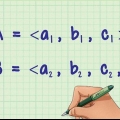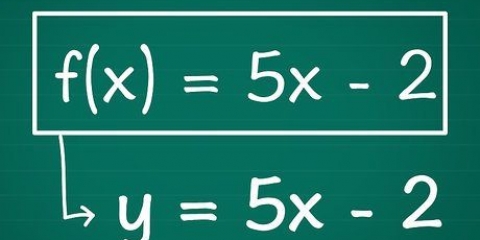Trova l'Angolo Tra Due Vettori

Contenuto

Passi
Consigli

Matematici e fisici spesso devono trovare l`angolo tra due dati vettori. Sebbene sia facile trovare l`angolo tra due vettori sullo stesso piano graficamente, può essere un po` più complicato nello spazio o in tre dimensioni. Questo articolo spiega il metodo da utilizzare per trovare l`angolo tra due vettori nel piano o nello spazio.

Passi

Metodo 1 di 4: Determina i vettori

1. Determina i vettori necessari per trovare l`angolo. Prendi i due vettori A e OQ che si intersecano nel punto O e calcolare l`angolo MOQ. Devi usare i vettori A e OQ usare, non farlo MO o QO. Nel caso in cui MO è noto, moltiplicalo per -1 per ottenere A ottenere.

Metodo 2 di 4: trova il prodotto scalare

Trova il prodotto scalare (o prodotto scalare) dei due vettori. Se non sai come calcolare il prodotto scalare di due vettori, continua a leggere:

1. Determina le componenti del vettore in ciascuna direzione. Quando i vettori sono elencati in una tabella, la prima riga rappresenta solitamente l`asse x, la seconda riga rappresenta l`asse y e la terza rappresenta l`asse z. Se il vettore è scritto nella forma xio + yJ + zK, quindi impostare i coefficienti di io, io, e K la grandezza delle componenti lungo gli assi x, yez (io, io, e K sono i vettori lungo gli assi x, yez).

2. Moltiplica le componenti di entrambi i vettori lungo l`asse x. Quindi moltiplica le componenti di entrambi i vettori lungo l`asse y e fai lo stesso per le componenti lungo l`asse z.

3. Aggiungi i tre prodotti insieme. Questo è il prodotto scalare di entrambi i vettori. Il prodotto scalare, o "prodotto interno", di due vettori è un numero molto utile in geometria e fisica. Per il momento utilizziamo questo prodotto solo come strumento per calcolare l`angolo tra due vettori. In un vettore bidimensionale, la componente lungo l`asse z è zero, quindi il prodotto scalare può essere trovato considerando solo le componenti lungo l`asse x e y.

Metodo 3 di 4: Calcola la dimensione

1. Calcola la grandezza dei due vettori. Calcolare la grandezza dei due vettori, usando la formula a=b+c+d, per cui un è la grandezza del vettore, e avanti Cristo, e D la dimensione dei componenti nelle tre diverse direzioni. In piano D essere uguale a zero.

Metodo 4 di 4: = Trova l`angolo

1. Usa i valori calcolati sopra in questa formula: cosθ = a.b / |a||b|

2. Ricava da questo il coseno inverso.

3. Finito.

Consigli

È possibile utilizzare questo metodo per calcolare l`angolo nei grafici 3D o x-y-z trattando i lati come vettori e trattando il vettore come vettori liberi.