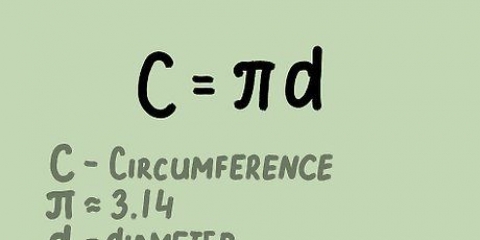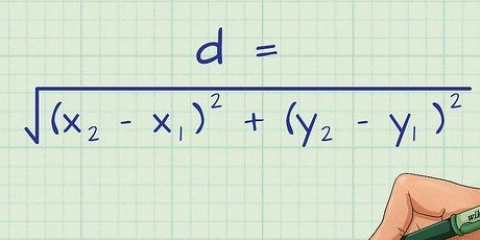Calcolare con i Vettori

Contenuto

Passi
Consigli

I vettori sono quantità costituite da una grandezza e una direzione (ad esempio: vettore di velocità o velocità vettoriale, accelerazione e spostamento), al contrario degli scalari, che hanno solo una grandezza (come velocità, distanza ed energia). Mentre gli scalari possono essere sommati in base alle loro dimensioni (ad es. 5 kJ + 6kJ = 11kJ), i vettori sono un po` più complicati da calcolare con. Vedere il passaggio 1 di seguito per ulteriori informazioni sui modi per farlo.

Passi

Metodo 1 di 3: addizione e sottrazione di vettori

Immagine intitolata Aggiungi o sottrai vettori Step 1

1. Esprimi le dimensioni di un vettore usando la notazione vettoriale. Poiché i vettori hanno una grandezza e una direzione, di solito è facile scomporli nelle loro dimensioni x, y e/o z. Queste dimensioni sono solitamente espresse in una notazione equivalente a descrivere un punto in un sistema di coordinate (es.

Nota che i vettori possono essere 1, 2 o 3 dimensioni. Quindi, i vettori possono avere una componente x, una componente xey o una componente x, y ecc. Il nostro esempio di seguito riguarda i vettori tridimensionali, ma il processo è simile a quello del piano o di una linea.

Supponiamo di avere due vettori tridimensionali, il vettore A e il vettore B. Possiamo scrivere questi vettori in notazione vettoriale come A =

Immagine intitolata Aggiungi o sottrai vettori Step 2

2. Per sommare due vettori, somma i componenti. Se si conoscono le componenti di due vettori, è possibile determinare i vettori sommando le componenti corrispondenti. In altre parole, aggiungi la componente x del primo vettore alla componente x del secondo e fai lo stesso per y e z. Le risposte che ottieni aggiungendo le componenti x, yez dei vettori originali sono le componenti x, yez del nuovo vettore.

In parole generali, A+B =

Sommiamo i due vettori A e B. A = <5, 9, -10> e B = <17, -3, -2>. A + B = <5+17, 9+-3, -10+-2>, o <22, 6, -12>.

Immagine intitolata Aggiungi o sottrai vettori Step 3

3. Per sottrarre due vettori, sottrai i loro componenti. Quindi lo stesso dell`addizione, ma al contrario.Se si conoscono le componenti di due vettori, sottrarre un vettore dall`altro non è altro che sottrarre le componenti.

In parole generali, AB =

Sottraiamo i due vettori A e B. A = <18, 5, 3> e B = <-10, 9, -10>. A - B = <18--10, 5-9, 3--10>, o <28, -4, 13>.

Metodo 2 di 3: addizione e sottrazione usando il metodo del back-end

Immagine intitolata Aggiungi o sottrai vettori Step 4

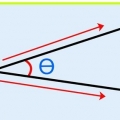
1. Indica i vettori con una freccia. Poiché i vettori hanno una grandezza e una direzione, puoi indicarli con una freccia. In altre parole, hanno a "punto di partenza" e un "punto finale", che punta nella direzione del vettore, con la grandezza del vettore indicata dalla freccia.

Quando si disegna un vettore in scala, è necessario misurare attentamente gli angoli. Gli angoli sbagliati danno come risultato una risposta sbagliata con questo metodo.

Immagine intitolata Aggiungi o sottrai vettori Step 5

2. Disegna le frecce in ordine di coda. La punta della freccia è posizionata contro la coda della freccia successiva. Dal momento che stai aggiungendo solo due vettori, questo è tutto ciò che devi fare per trovare il vettore risultante.

Si noti che l`ordine in cui si disegnano i vettori non è importante, purché si assuma che si utilizzi sempre lo stesso punto di partenza. Vettore A + Vettore B = Vettore B + Vettore A

Immagine intitolata Aggiungi o sottrai vettori Step 6

3. Per sottrarre fai il vettore "negativo". Sottrarre vettori con questo metodo visivo è relativamente facile. Inverti la direzione del vettore, ma mantieni la stessa dimensione e aggiungila usando il metodo dalla testa alla coda come al solito. In altre parole, per sottrarre un vettore, ruoti il vettore di 180 e aggiungi.

Immagine intitolata Aggiungi o sottrai vettori Step 7

4. Se vuoi aggiungere o sottrarre più di due vettori, collega tutti quei vettori uno dopo l`altro usando il metodo della parte posteriore. L`ordine non ha importanza. Puoi usarlo per qualsiasi numero di vettori.

5. Disegna un nuovo vettore dalla coda del primo vettore alla testa dell`ultimo. Che tu stia lavorando con 2 o 100 vettori, il vettore che si estende dal punto iniziale (la coda del tuo primo vettore) al punto finale dei vettori aggiunti (la testa del tuo ultimo vettore) è il risultato vettore o la somma di tutti i vettori. Si noti che questo vettore è uguale al vettore ottenuto sommando le componenti x, y e/o z di tutti i vettori.

Immagine intitolata Aggiungi o sottrai vettori Step 8

Poiché hai disegnato tutti i vettori in scala e hai misurato esattamente gli angoli, puoi trovare la grandezza del vettore risultante misurando la lunghezza. Puoi anche misurare l`angolo che questa risultante forma con un vettore specifico o con l`orizzontale/verticale ecc. per trovare la direzione.

Dal momento che non hai disegnato tutti i vettori in scala, probabilmente dovrai calcolare la grandezza del risultante usando la trigonometria. Usa la regola seno o coseno per questo. Dato che stai aggiungendo più di due vettori, è utile aggiungerne prima due, quindi aggiungere la loro risultante al terzo vettore e così via. Vedere la sezione successiva per ulteriori informazioni.

Immagine intitolata Aggiungi o sottrai vettori Step 9

6. Visualizza il vettore risultante per dimensione e direzione. I vettori sono determinati dalla loro lunghezza e direzione. Come affermato sopra, supponendo che tu abbia disegnato i vettori con precisione, la grandezza del vettore è uguale alla sua lunghezza e direzione e il suo angolo è relativo alla verticale, orizzontale, ecc. Usa le unità dei vettori che hai sommato per scegliere le unità per la grandezza del vettore risultante.

Ad esempio, se i vettori che abbiamo aggiunto rappresentano un vettore di velocità in ms, allora potremmo rappresentare il vettore risultante come "un vettore di velocità di X ms a y rispetto all`orizzontale".

Metodo 3 di 3: Somma e sottrazione di vettori determinando le componenti

Immagine intitolata Aggiungi o sottrai vettori Step 10

1. Usa la trigonometria per trovare i componenti del vettore. Hai bisogno della grandezza e della direzione relative all`orizzontale o alla verticale e devi avere una certa conoscenza pratica della trigonometria. Supponiamo di avere un vettore 2D. Per prima cosa fai dei vettori l`ipotenusa di un triangolo rettangolo, con gli altri due lati paralleli agli assi xey. Puoi pensare a questi due lati come vettori testa a coda che, se sommati insieme, producono il vettore originale.

Le lunghezze dei due lati sono uguali alle grandezze delle componenti x e y del tuo vettore e possono essere calcolate usando la trigonometria. Se x è la grandezza del vettore, allora il lato adiacente all`angolo del vettore (rispetto all`orizzontale, verticale, ecc.) uguale a xcos(θ), mentre il contrario è uguale a xsin(θ).
È anche importante considerare l`orientamento dei componenti. Se il componente punta nella direzione negativa di uno degli assi, ottiene un segno meno. Ad esempio, se un componente punta a sinistra o in basso nel piano, ottiene un segno meno.
Ad esempio, supponiamo di avere un vettore di magnitudine 3 e una direzione 135 rispetto all`orizzontale. Con queste informazioni possiamo determinare che la componente x è uguale a 3cos(135) = -2.12 e la componente y è 3sin(135) = 2.12

Immagine intitolata Aggiungi o sottrai vettori Step 11

2. Somma le componenti corrispondenti di due o più vettori. Quando hai trovato le componenti di tutti i vettori, somma semplicemente le grandezze per trovare le componenti del tuo vettore risultante. Per prima cosa somma le dimensioni delle componenti orizzontali (parallele all`asse x). Quindi aggiungi le dimensioni delle componenti verticali (parallele all`asse y). Se un componente ha un segno meno (-) davanti ad esso, la sua dimensione viene sottratta. Le risposte che ottieni sono i componenti del tuo vettore risultante.

Ad esempio, prendiamo il vettore dal passaggio precedente, <-2.12 e 2.12>, e aggiungilo al vettore <5.78 e -9>. In questo caso, il nostro vettore risultante è <-2.12+5.78 e 2.12-9>, o <3.66 e-6.88>.

Immagine intitolata Aggiungi o sottrai vettori Step 12

3. Calcola la grandezza del vettore risultante usando il teorema di Pitagora. Con questa affermazione, c=a+b, riesci a trovare la lunghezza dei lati dei triangoli rettangoli?. Poiché il triangolo formato dal vettore risultante e dai suoi componenti è un triangolo rettangolo, possiamo usare questo teorema per trovare la lunghezza del vettore e quindi la sua grandezza. Di C come la grandezza del vettore risultante che stai cercando di trovare, diciamo un in come la dimensione del componente x e B come grandezza della componente y. Risolvi con l`algebra.

Per trovare la grandezza del vettore di cui abbiamo determinato i componenti nel passaggio precedente, <3.66 e -6.88>, usiamo il teorema di Pitagora. Risolvi come segue:

c=(3.66)+(-6.88)

c=13.40+47.33

c=√60.73 = 7.79

Immagine intitolata Aggiungi o sottrai vettori Step 13

4. Calcola la direzione della risultante con la tangente. Infine, determiniamo la direzione del vettore risultante. Usa la formula θ=abbronzatura(b/a), dove θ è l`angolo che la risultante forma con l`asse x rispetto all`orizzontale, dove b è la grandezza della componente y e a è la grandezza della componente x.

Per determinare la direzione del nostro vettore di esempio, utilizziamo θ=tan(b/a).

θ=abbronzatura(-6.88/3.66)

θ=abbronzatura(-1.88)

θ=-61.99

Immagine intitolata Aggiungi o sottrai vettori Step 14

5. Visualizza il vettore risultante per dimensione e direzione. Come indicato sopra, i vettori sono definiti dalla loro magnitudine e direzione. Assicurati di utilizzare le unità corrette per la dimensione del vettore.

Ad esempio, se il vettore di esempio rappresenta una forza (in Newton), possiamo scriverla come "un potere di 7.79 N su -61.99 dall`orizzontale".

Consigli

I vettori non devono essere confusi con le dimensioni.
Puoi trovare la dimensione di un vettore nello spazio dalla formula a=b+c+d da usare, dove un è la grandezza del vettore e avanti Cristo e D i componenti in ogni direzione.
Vettori rappresentati come xio + yJ + zK possono essere sommati o sottratti semplicemente sommando o sottraendo i coefficienti dei tre vettori. La risposta è quindi anche nella forma i, j, k.
I vettori di colonna possono essere aggiunti e sottratti, aggiungendo o sottraendo i valori in ogni riga.