Calcolo delle Forze in Fisica: 8 Passaggi (con Immagini)

Contenuto

Passi
- Metodo 1 di 2: Determinazione della tensione su un singolo cavo
- Metodo 2 di 2: Calcolo della tensione su più accordi

In fisica, la tensione è la forza esercitata da una corda, una corda, un cavo o un oggetto simile su uno o più altri oggetti. Tutto ciò che viene tirato è sospeso, sostenuto o attaccato a una fune.D. oscilla, è soggetto alla forza della tensione. Come altre forze, la tensione può accelerare o deformare gli oggetti. Saper calcolare la tensione è un`abilità importante per gli studenti di fisica, ma anche per ingegneri e architetti. Dopotutto, per progettare edifici sicuri, devono sapere esattamente se la tensione su un cavo può sopportare il carico di un oggetto. Continua a leggere al passaggio 1 per imparare a calcolare lo stress in vari sistemi fisici.

Passi

Metodo 1 di 2: Determinazione della tensione su un singolo cavo

Immagine titolata Calculate Tension in Physics Step 1

1. Determina le forze su ciascun lato del filo. La tensione in un dato filo di una fune è la somma di tutte le forze che tirano la fune da entrambe le estremità. Non dimenticare: forza = massa × accelerazione. Supponiamo che la fune sia tesa strettamente, quindi qualsiasi cambiamento nell`accelerazione o nella massa degli oggetti che la fune supporta causerà un cambiamento nella tensione nella fune. Dimentica la costante accelerazione dovuta alla forza di gravità nessuno dei due – anche quando un sistema è fermo, ogni componente è esposto alla gravità. La tensione in una particolare fune può essere espressa come T = (m × g) + (m × a), dove "G" l`accelerazione è dovuta alla gravità di qualsiasi oggetto sostenuto dalla fune, e "un" è qualsiasi altra accelerazione su qualsiasi oggetto supportato dalla fune.

Per semplicità, possiamo supporre di avere a che fare con afilo ideale – in altre parole, che la fune, il cavo, ecc. è sottile e senza massa e non può allungarsi o rompersi.
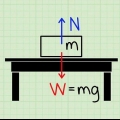
Un esempio: supponiamo di avere un sistema in cui una massa pende da una trave di legno, fissata con un`unica fune (vedi foto). Eppure le masse muovono ancora la corda: l`intero sistema è fermo. Ora sappiamo che la massa è in equilibrio, dove la forza di tensione è uguale alla forza gravitazionale sulla massa. In altre parole, Tensione (F_T) = Forza o Gravità (F_G) = m × g.

Supponiamo di avere una massa di 10 kg, allora vale: tensione = 10 kg × 9,8 m/s = 98 Newton.

Immagine titolata Calculate Tension in Physics Step 2

2. Fai attenzione all`accelerazione. La gravità non è l`unica forza che influenza la tensione di una fune: qualsiasi forza può essere associata all`accelerazione di un oggetto a cui è collegata la fune. Se un oggetto sospeso viene accelerato da una forza sulla fune o sul cavo, la forza causata dall`accelerazione (massa × accelerazione) viene aggiunta alla tensione causata dalla massa dell`oggetto.

Supponiamo nel nostro esempio che la massa di 10 kg sia appesa ad una fune, che non è attaccata ad una trave, ma serve per sollevare la massa con un`accelerazione di 1 m/s. In casi come questo dobbiamo tenere conto non solo dell`accelerazione sulla massa, ma anche della forza gravitazionale, risolvendo questo come segue:

F_T = F_G + m × a

F_T = 98 + 10 kg × 1 m/s

F_T = 108 Newton.

Immagine titolata Calculate Tension in Physics Step 3

3. Prendi in considerazione anche un ingranaggio circolare. Un oggetto che viene ruotato attorno a un punto centrale di una fune (come un pendolo) esercita una tensione sulla fune causata dalla forza centripeta. La forza centripeta è la forza che la corda esercita su un oggetto tirandolo verso l`interno "Tiro", in modo che l`oggetto continui a muoversi in un arco, invece di andare dritto. Più velocemente si muove l`oggetto, maggiore è la forza centripeta. forza centripeta (F_C) è uguale a m × v/r dove "m" è uguale alla massa, "v" è la velocità e "R" è il raggio del cerchio, cioè il percorso in cui l`oggetto si muove.

Poiché la direzione e l`entità della forza centripeta cambiano quando l`oggetto sulla fune si muove e la velocità cambia, così cambia la tensione totale nella fune, che tira sempre parallela alla fune verso il punto centrale. Ricorda che la costante gravitazionale attira l`oggetto. Quindi, se un oggetto viene lanciato in posizione verticale, la tensione totale è la maggiore nella parte inferiore della traiettoria dell`oggetto (nel caso di un orologio a pendolo, questo è anche chiamato equilibrio), dove l`oggetto si muove più velocemente. La tensione è minima nella parte superiore del movimento circolare, dove la velocità è più bassa.

Supponiamo nell`esempio che l`oggetto oscilli come un pendolo. La fune è lunga 1,5 metri e la massa si muove ad una velocità di 2 m/s nel punto più basso. Se vogliamo calcolare la tensione in quel punto, il punto in cui la velocità è massima, dobbiamo prima vedere che la tensione dovuta alla gravità in questo punto è la stessa di quando il pendolo è fermo - 98 Newton. Per trovare la forza centripeta, calcoliamo come segue:

F_C = m × f/r

F_C = 10 × 2/1.5

F_C =10 × 2,67 = 26,7 Newton.

Quindi, la tensione totale è 98 + 26,7 = 124,7 Newton.

Immagine titolata Calculate Tension in Physics Step 4

4. Comprendi che la tensione dovuta alla gravità cambia durante il periodo del pendolo. Come accennato in precedenza, sia la direzione che l`entità della forza centripeta cambiano quando un oggetto oscilla. Ma sebbene la gravità rimanga costante, il tensione per gravità anche cambiare. Come un oggetto oscillante non parte inferiore dell`oscillazione del pendolo (il punto di equilibrio), quindi la gravità tira verso il basso, ma la tensione tira sull`oggetto ad angolo. Per questo motivo, la tensione cancellerà parte della forza gravitazionale, ma non completamente.

Spezzare la gravità in due vettori può aiutarti a visualizzare meglio questo concetto. In qualsiasi punto dell`arco del movimento di un oggetto oscillante, la fune forma un angolo di "θ" con la retta passante per l`equilibrio e il punto centrale della rotazione. Mentre la fune oscilla, puoi dividere la forza di gravità (m × g) in 2 vettori: mgsin(θ) è la tangente all`arco nella direzione dell`equilibrio e mgcos(θ), il parallelo alla forza di tensione nel direzione opposta. La tensione deve solo opporsi a mgcos(θ) - la forza che si oppone - non alla piena forza di gravità (tranne nel punto di equilibrio, quando è uguale alla tensione).

Supponiamo che il pendolo formi un angolo di 15 gradi con la verticale e quindi abbia una velocità di 1,5 m/s. Troviamo la tensione come segue:

Stress dovuto alla gravità (T_G) = 98cos(15) = 98(0,96) = 94,08 Newton

forza centripeta (F_C) = 10 × 1,5/1,5 = 10 × 1,5 = 15 Newton

Tensione totale = T_G + F_C = 94.08 + 15 = 109.08 Newton.

Immagine titolata Calculate Tension in Physics Step 5

5. Pensa anche all`attrito. Qualsiasi oggetto tirato attraverso una fune e che subisce l`attrito da un altro oggetto (o liquido) trasferisce questa forza di attrito alla tensione nella fune. La forza di attrito tra due oggetti viene calcolata allo stesso modo di qualsiasi altra situazione, con la seguente equazione: Forza di attrito F_R = (mu)N, dove mu è il coefficiente di attrito tra i due oggetti e dove N è la forza normale tra i due oggetti (la forza con cui si premono l`uno contro l`altro). Si noti che l`attrito statico - l`attrito che si verifica quando si tenta di spostare un oggetto fermo - è diverso dall`attrito cinetico, l`attrito che si verifica quando si tenta di mantenere in movimento un oggetto in movimento.

Supponiamo che la massa di 10 kg non oscilli più, ma venga trascinata orizzontalmente a terra e su una fune. Ora diciamo che il terreno ha un coefficiente di attrito dinamico di 0,5 e che la massa si muove a velocità costante, ma vogliamo accelerarla a 1 m/s. Questo nuovo incarico rivela due importanti cambiamenti: il primo è che non abbiamo più bisogno di calcolare la tensione dovuta alla gravità, perché la fune non sostiene più la massa e contrasta la forza. Ora dobbiamo prendere in considerazione la forza di attrito e la sollecitazione risultante, nonché la sollecitazione causata dall`accelerazione dell`oggetto. Risolviamo questo come segue:

Forza normale (N) = 10 kg × 9.8 (accelerazione di gravità) = 98 N

Forza di attrito dinamico (F_R) = 0.5 × 98 N = 49 Newton

Forza di accelerazione (F_un) = 10 kg × 1 m/s = 10 Newton

Tensione totale = F_R + F_un = 49 + 10 = 59 Newton.

Metodo 2 di 2: Calcolo della tensione su più accordi

Immagine titolata Calculate Tension in Physics Step 6

1. Sollevamento di carichi verticali paralleli con una puleggia. Una puleggia è una macchina semplice costituita da una ruota sospesa che consente alla forza di tensione in una fune di cambiare direzione. In una configurazione semplice, la fune o il cavo scorre da una massa sospesa verso l`alto attraverso la puleggia, quindi verso il basso verso un`altra massa, dandoti due lunghezze di fune. Ma la tensione in entrambe le parti della fune è la stessa, anche se masse di dimensioni diverse pendono da entrambe le estremità della fune. In un sistema di due masse sospese ad una puleggia, la tensione è pari a 2g(m₁)(m₂)/(m₂+m₁), per cui "G" l`accelerazione è dovuta alla gravità, "m₁" la massa dell`oggetto 1 e "m₂" la massa dell`oggetto 2.

Si noti che assumiamo a "puleggia ideale – nessuna massa, nessun attrito e pulegge che non possono rompersi, deformarsi o staccarsi dal soffitto.
Supponiamo di avere due masse appese ad una puleggia, su funi parallele. Il peso 1 ha una massa di 10 kg e il peso 2 ha una massa di 5 kg. In questo caso troviamo la tensione come segue:

T = 2 g(m₁)(m₂)/(m₂+m₁)
T = 2(9,8)(10)(5)/(5 + 10)
T = 19,6(50)/(15)
T = 980/15
T = 65.33 Newton.

Si noti che poiché una massa è più pesante dell`altra, il sistema accelererà, con i 10 kg che si spostano verso il basso e i 5 kg che si spostano verso l`alto.

2. Sollevamento pesi con carrucola su funi verticali ma non parallele. Le pulegge sono spesso utilizzate per ottenere la tensione in una direzione diversa da quella su o giù. Ad esempio, se una massa pende verticalmente da un`estremità della fune, mentre una seconda massa è legata su un pendio all`altra estremità, questo sistema di pulegge non parallele assumerà la forma di un triangolo i cui vertici sono la prima massa, la seconda massa e la puleggia stessa. In questo caso la tensione nella fune è determinata sia dalla gravità sulla massa sia dalla componente della forza di trazione agente parallelamente alla porzione diagonale della fune.

Supponiamo di avere un sistema con una massa di 10 kg (m₁), collegati verticalmente, tramite una carrucola, con una massa di 5 kg (m₂) su una pendenza di 60 gradi (supponiamo che la pendenza sia priva di attrito). Per trovare la tensione nella fune è più facile essere i primi a formulare equazioni per le forze che accelerano le masse. Procedi come segue:

La massa sospesa è più pesante e non dobbiamo tenere conto dell`attrito, quindi sappiamo che c`è un`accelerazione verso il basso. Ma la tensione nella fune tira su la massa, quindi calcoliamo la forza netta sulla fune come segue: F = m₁(g) - T, o 10(9.8) - T = 98 - T.

Sappiamo che la massa accelererà lungo il pendio. Poiché il pendio è privo di attrito, sappiamo che la tensione trascina la massa su per il pendio, trattenuta solo dalla massa del peso stesso. La componente della forza che spinge il peso verso il basso è calcolata da mgsin(θ), quindi nel nostro caso possiamo dire che il peso in salita accelera la pendenza della forza netta F = T - m₂(g)peccato(60) = T - 5(9.8)(.87) = T - 42.63.

L`accelerazione delle due masse è la stessa, quindi abbiamo (98 - T)/m₁ = T - 42.63/mq₂. Dopo una semplice algebra otteniamo T = 61.09 Newton.

Immagine titolata Calculate Tension in Physics Step 8

3. Utilizzo di più cavi per appendere un oggetto. Infine, consideriamo il caso in cui un oggetto si blocca su a "A forma di Y" sistema di funi: due funi sono fissate al soffitto e si incontrano in un punto centrale, dove un peso pende da una terza fune. La tensione nella terza fune è ovvia: questa è semplicemente la tensione risultante a causa della gravità. Le tensioni nelle altre due funi sono diverse e, sommate, dovrebbero essere uguali alla gravità in direzione verticale e verso l`alto, e pari a zero in direzione orizzontale (supponendo che il sistema sia fermo). La tensione nelle funi è influenzata dalla massa dell`oggetto sospeso e dall`angolo di ciascuna fune rispetto al soffitto.

Supponiamo in questo sistema a Y, che l`oggetto abbia un peso di 10 kg e che le due corde superiori formino un angolo con il soffitto di 30 gradi e 60 gradi. Se vogliamo trovare la tensione in ciascuna delle corde superiori, dobbiamo considerare le componenti verticali e orizzontali della tensione per ciascuna corda. Le due funi in questo esempio pendono perpendicolarmente l`una all`altra, facilitando il calcolo di queste sollecitazioni, secondo le definizioni delle funzioni trigonometriche. Quindi come segue:

Il rapporto tra t₁ o t₂ e T = m(g) è uguale al seno dell`angolo tra ciascuna fune di supporto e il soffitto. per t₁ è sin(30) = 0,5, mentre per T₂ sostiene che sin(60) = 0,87.

Moltiplicare la tensione nella fune inferiore (T = mg) per il seno di ciascun angolo, per ottenere T₁ e T₂ trovare.

T₁ =0,5 × m(g) =0,5 × 10(9,8) = 49 Newton.

T₂ =0,87 × m(g) =0,87 × 10(9,8) = 85,26 Newton.