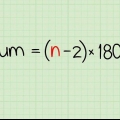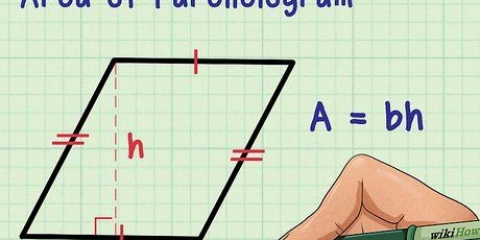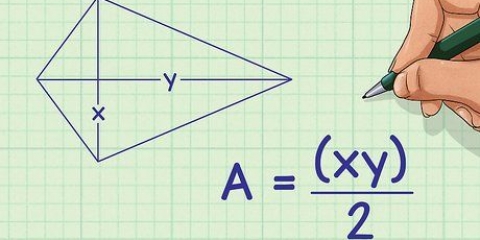Gli angoli in un triangolo (un poligono a 3 lati) totalizzano 180 gradi. Gli angoli in un quadrilatero (un poligono a 4 lati) totalizzano 360 gradi. Gli angoli in un pentagono (un poligono a 5 lati) totalizzano 540 gradi. Gli angoli in un esagono (un poligono a 6 lati) totalizzano 720 gradi. Gli angoli in un ottagono (un poligono a 8 lati) totalizzano 1080 gradi. 
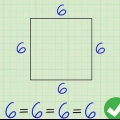
Se il poligono è un poligono regolare, basta dividere il totale di tutti gli angoli per il numero di angoli. Quindi qualsiasi angolo in un triangolo equilatero è 180/3=60 gradi e qualsiasi angolo di un quadrato è 360/4=90 gradi. (Sebbene per definizione un rettangolo non sia un poligono regolare, tutti gli angoli sono anche retti, e quindi 90 gradi). Se un poligono non è un poligono regolare, dovrai conoscere la grandezza degli altri angoli per calcolare la grandezza dell`angolo sconosciuto. vai al passaggio successivo. 
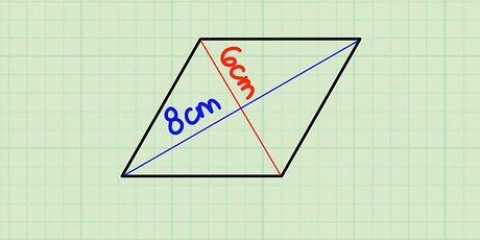
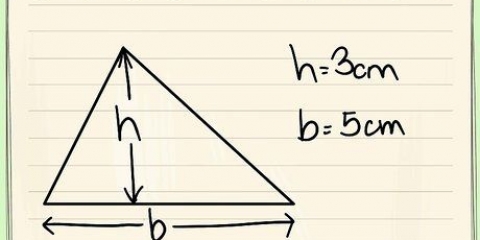
Se due degli angoli di un triangolo sono 60 e 80 gradi, somma questi angoli insieme (60 + 80=140). Quindi sottrai questa somma dal totale degli angoli di un triangolo, 180 gradi: 180-140=40 gradi. (Un tale triangolo, in cui tutti gli angoli sono diversi, è chiamato triangolo scaleno). Puoi scrivere il metodo sopra come una formula: un=180 – (B + C), per cui un è l`angolo che vuoi determinare, e B e C gli angoli conosciuti. Per i poligoni con più di 3 lati, sostituisci "180" con il totale degli angoli come specifico per quel poligono e aggiungi un termine diverso per ogni angolo noto aggiuntivo. Per alcuni poligoni è possibile una "soluzione più rapida" per determinare l`angolo sconosciuto. Un triangolo isoscele è un triangolo con due lati di uguale lunghezza e due angoli di uguale grandezza. Un parallelogramma è un quadrilatero con lati opposti di uguale lunghezza e angoli diagonalmente opposti di uguale grandezza. 

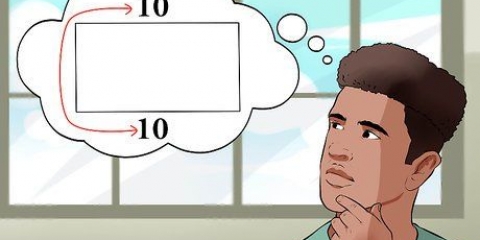
Se conosci la lunghezza del lato opposto (rispetto all`angolo) e la lunghezza dell`ipotenusa (il lato opposto all`angolo retto), usa la funzione seno (la lunghezza del lato opposto divisa per la lunghezza dell`ipotenusa). seta). Se conosci la lunghezza del lato rettangolare adiacente e la lunghezza dell`ipotenusa, puoi utilizzare la funzione coseno (la lunghezza del lato adiacente divisa per la lunghezza dell`ipotenusa). Se conosci le lunghezze dei lati opposti e adiacenti, puoi usare la funzione tangente (la lunghezza del lato opposto divisa per la lunghezza del lato adiacente). 
Dividendo il valore opposto 5 per l`ipotenusa (l`ipotenusa) 10 si ottiene la frazione 5 / 10=0,5. 
Nei giorni precedenti alle calcolatrici, dovresti consultare una tabella stampata di valori per seno, coseno e tangente di angoli da 0 a 90 gradi. Segui la colonna del seno finché non trovi il valore `0,5` e poi trova l`angolo che corrisponde a quel valore del seno. Se hai una calcolatrice con funzioni trigonometriche, puoi inserire il seno come valore (se non hai già usato la calcolatrice per dividere il contrario per l`ipotenusa per trovare questo valore) e quindi premere il tasto o i tasti appropriati. A seconda della marca della calcolatrice, premere un solo tasto etichettato `sin` o un tasto etichettato `Inv`, `2ndF` o `Shift` prima di premere il tasto `sin`. Qualunque sia il metodo utilizzato per risolvere questo esempio, in tutti i casi dovresti trovare un angolo di 30 gradi.
Calcola angoli
Contenuto
In geometria, un angolo è lo spazio tra due raggi o segmenti di linea che hanno lo stesso punto finale o vertice. Il modo più comune per misurare gli angoli è in gradi, dove un cerchio completo è di 360 gradi. Puoi calcolare l`angolo in un poligono se conosci la forma del poligono e la dimensione degli altri angoli oppure, nel caso di un triangolo rettangolo, se conosci la dimensione dei due lati.
Passi
Metodo 1 di 2: calcolo dell`angolo in un poligono

1. Conta il numero di lati del poligono.

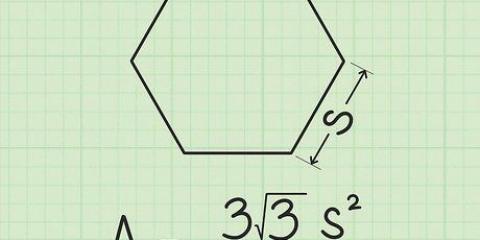
2. Trova la somma di tutti gli angoli del poligono. La formula per trovare la misura totale di tutti gli angoli interni in un poligono è (n – 2) x 180, dove n è il numero di lati, nonché il numero di angoli del poligono. Alcuni totali comuni degli angoli in un poligono sono:

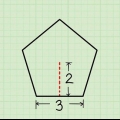
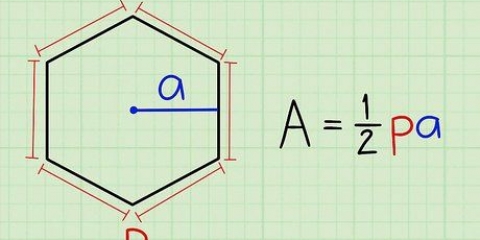
3. Determina se il poligono è un poligono regolare. Un poligono regolare è un poligono con tutti i lati della stessa lunghezza e tutti gli angoli della stessa dimensione. Triangoli e quadrati equilateri sono esempi di poligoni regolari, mentre il Pentagono a Washington DC è un esempio di pentagono regolare e un segnale di stop è un esempio di ottagono regolare.

4. Somma gli angoli noti del poligono e sottrai il totale dal totale di tutte le misure angolari del poligono. La maggior parte dei problemi di geometria simili funzionano con triangoli o quadrilateri perché ci sono meno numeri da elaborare, e così lo faremo.
Metodo 2 di 2: Calcola l`angolo in un triangolo rettangolo

1. Scopri cosa sai già. Un triangolo rettangolo è così chiamato perché uno dei suoi angoli è un angolo retto. È possibile determinare gli altri angoli se si conosce uno dei seguenti elementi:
- La dimensione del terzo angolo. In questo caso, puoi sommare la dimensione dell`angolo a 90, il numero di gradi dell`angolo retto, quindi sottrarre il totale da 180.
- La dimensione di due lati del triangolo. In questo caso è possibile determinare l`ampiezza dell`angolo utilizzando la trigonometria.

2. Determina quale funzione trigonometrica utilizzare. Le funzioni trigonometriche sono rapporti tra due dei tre lati di un triangolo. Sebbene ci siano sei funzioni trigonometriche, le tre seguenti sono più comunemente utilizzate:

3. Trova il rapporto tra i due lati noti. Ai fini di questo esempio, supponiamo che il lato opposto all`angolo abbia una lunghezza di 5 e che l`ipotenusa abbia una lunghezza di 10. Poiché sono così dati l`opposto e l`ipotenusa, il rapporto di cui ci occupiamo qui è quello del seno.

4. Trova l`angolo corrispondente al rapporto della funzione trigonometrica. Poiché stiamo usando il seno per trovare l`angolo, l`angolo che stiamo cercando è chiamato arcoseno o seno inverso. Ci sono due modi per trovarlo:
Consigli
- Gli angoli sono indicati dal numero di gradi che misurano. Come accennato in precedenza, un angolo retto ha 90 gradi. Un angolo maggiore di 0 ma minore di 90 gradi è un angolo acuto. Un angolo maggiore di 90 ma minore di 180 gradi è un angolo ottuso. Un angolo di 180 gradi è un angolo retto, mentre un angolo maggiore di 180 gradi è un angolo rientrante.
- Due angoli con un totale di 90 gradi sono chiamati angoli complementari (i due angoli diversi dall`angolo retto in un triangolo rettangolo sono angoli complementari). Due angoli i cui angoli sommati fino a 180 gradi sono chiamati angoli supplementari.
Necessità
- Tavole trigonometriche o calcolatrice con funzioni trigonometriche
Articoli sull'argomento "Calcola angoli"
Condividi sui social network:
Popolare