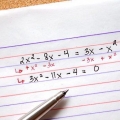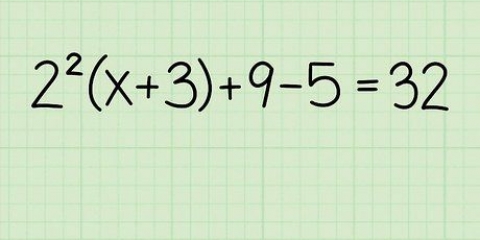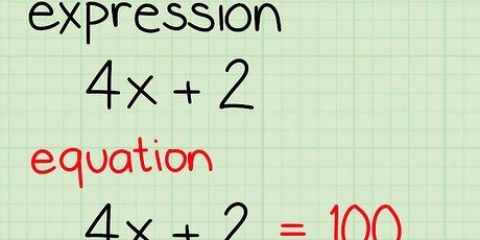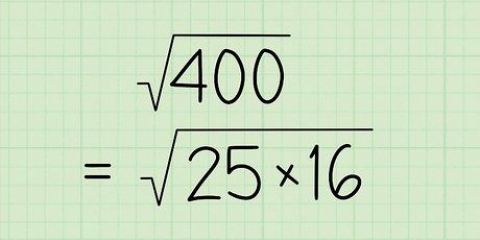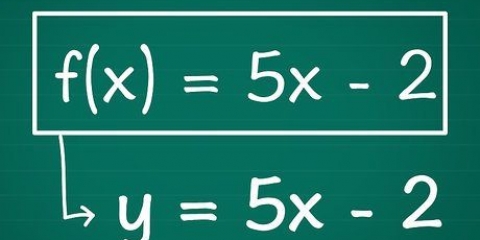3(x - 2/3) =
3(x - 2/3)(x -2/3) = 3[(x -2/3x -2/3x + 4/9)] 3(x - 4/3x + 4/9) 
-4/3 + 15/3 = 11/3.










Piazza spaccata
Contenuto
La quadratura è una tecnica utile per riscrivere un`equazione quadratica rendendo più facile la supervisione e la risoluzione. Puoi riscrivere un quadrato riorganizzandolo in pezzi più gestibili.
Passi
Metodo 1 di 2: Parte prima: riscrivere un`equazione standard

1. Scrivi l`equazione. Supponiamo di voler risolvere la seguente equazione: 3x - 4x + 5.

2. Rimuovere il coefficiente dall`equazione. Metti le 3 parentesi esterne e dividi ogni termine tranne la costante per 3. 3x diviso per 3 è x e 4x diviso per 3 è 4/3x. Quindi la nuova equazione si presenta così: 3(x - 4/3x) + 5. Il 5 è fuori dalle parentesi perché non l`hai diviso per 3.

3. Dividi il secondo termine per 2 e quadra. Il secondo termine, chiamato anche il B-termine nell`equazione, è 4/3. Dimezza il secondo mandato. 4/3 ÷ 2, o 4/3 x 1/2, equivale a 2/3. Al quadrato questo termine moltiplicando sia il numeratore che il denominatore per se stessi. (2/3) = 4/9. Scrivi questo termine.

4. Addizione e sottrazione. L`hai capito"aggiuntivo" termine necessario per convertire i primi tre termini dell`equazione in un quadrato. Ma ricorda che hai aggiunto questo termine sottraendolo anche dall`equazione. Ovviamente non fa poca differenza combinare semplicemente di nuovo i termini, quindi tornerai da dove hai iniziato. La nuova equazione dovrebbe ora apparire così: 3( x - 4/3 x + 4/9 - 4/9) + 5.

5. Ottieni il termine che hai sottratto fuori dalle parentesi. Poiché stai già lavorando con il 3 fuori parentesi, non è possibile mettere solo -4/9 fuori parentesi. Per prima cosa devi moltiplicarlo per 3. -4/9 x 3 = -12/9 o -4/3. Se hai a che fare con un`equazione che contiene solo un coefficiente 1 dix, puoi saltare questo passaggio.

6. Converti i termini tra parentesi in un quadrato. La tua equazione ora è simile a questa: 3(x -4/3x +4/9). Hai lavorato davanti a dietro per ottenere 4/9, che in realtà è un altro modo per trovare il fattore che completa il quadrato. Quindi puoi riscrivere questi termini come: 3(x - 2/3). Puoi verificarlo moltiplicando dove vedrai che ottieni di nuovo la stessa equazione originale della risposta.


7. Unisci le costanti. Ora hai due costanti, 3(x - 2/3) - 4/3 + 5. Tutto quello che devi fare ora è aggiungere -4/3 a 5 e questo dà 11/3 come risposta. Lo fai dando loro lo stesso denominatore: -4/3 e 15/3, quindi sommando entrambi i numeratori per ottenere 11, mantenendo il denominatore uguale a 3.


8. Scrivi l`equazione in un`altra forma. Ora hai finito. L`equazione finale è 3(x - 2/3) + 11/3. Puoi eliminare il 3 dividendo l`equazione per 3, lasciandoti con la seguente equazione:(x - 2/3) + 11/9.Ora hai scritto con successo l`equazione in un`altra forma: a( x - h ) + k, per cui K la costante è.
Metodo 2 di 2: Parte seconda: Risolvere un`equazione quadratica

1. Nota il compito. Supponiamo di voler risolvere la seguente equazione: 3x + 4x + 5 = 6

2. Somma le costanti e mettile a sinistra del segno di uguale. I termini costanti sono quei termini senza una variabile. In questo caso hai 5 a sinistra e 6 a destra. Vuoi spostare 6 a sinistra, quindi sottrai 6 da entrambi i lati dell`equazione. Questo lascia 0 a destra (6-6) e -1 a sinistra (5-6). L`equazione ora appare così: 3x + 4x - 1 = 0.

3. Prendi il coefficiente del quadrato fuori dalle parentesi. In questo caso, 3 è il coefficiente di x. Per escludere 3 dalle parentesi, rimuovi il 3, metti il termine rimanente tra parentesi e dividi ogni termine per 3. Quindi, 3x ÷ 3 = x, 4x ÷ 3 = 4/3x e 1 ÷ 3 = 1/3. L`equazione ora appare così: 3(x + 4/3x - 1/3) = 0.

4. Dividi per la costante che hai appena inserito tra parentesi. Con questo finalmente ti sbarazzi di quei fastidiosi 3 fuori parentesi. Dividendo ogni termine per 3, può essere eliminato senza modificare l`equazione. Ora hai: x + 4/3x - 1/3 = 0

5. Dividi il secondo termine per 2 e quadra. Ora prendi il secondo termine, 4/3, de B termine e dividere per 2. 4/3 2 o 4/3 x 1/2, è 4/6 o 2/3. E 2/3 al quadrato è 4/9. Quando hai finito con questo dovresti scriverlo a sinistra ea destra dell`equazione perché in pratica hai appena aggiunto un nuovo termine. Devi farlo su entrambi i lati dell`equazione. L`equazione ora appare così: x + 4/3 x + 2/3 - 1/3 = 2/3

6. Sposta la costante originale sul lato destro dell`equazione e aggiungila al termine già presente. Sposta la costante, -1/3, a destra per renderla 1/3. Aggiungi questo all`altro termine, 4/9 o 2/3. Trova il minimo comune multiplo in modo da poter sommare 1/3 e 4/9. Questo va così: 1/3 x 3/3 = 3/9. Ora aggiungi 3/9 a 4/9 in modo da avere 7/9 sul lato destro dell`equazione. Questo dà: x + 4/3 x + 2/3 = 4/9 + 1/3 e poi x + 4/3 x + 2/3 = 7/9.

7. Scrivi il lato sinistro dell`equazione come un quadrato. Dato che hai già usato una formula per trovare il termine mancante, la parte più difficile è già stata fatta. Tutto quello che devi fare è mettere la x e la metà del secondo coefficiente tra parentesi e quadrarlo, in questo modo :(x + 2/3). Si noti che la fattorizzazione del quadrato produce 3 termini: x + 4/3 x + 4/9. L`equazione ora appare così: (x + 2/3) = 7/9.

8. Prendi la radice quadrata di entrambi i membri dell`equazione. Sul lato sinistro dell`equazione, la radice quadrata di (x + 2/3) è uguale a x + 2/3. Il lato destro dà +/- (√7)/3. La radice quadrata del denominatore 9 è 3 e la radice quadrata di 7 è √7. Non dimenticare di scrivere +/- perché la radice quadrata di un numero può essere positiva o negativa.

9. Metti da parte la variabile. Per isolare la variabile x dal resto, sposta la costante 2/3 sul lato destro dell`equazione. Ora hai due possibili risposte per x:+/- (√7)/3 - 2/3. Queste sono le tue due risposte. Puoi lasciare così o elaborare la radice quadrata, se ti viene chiesta una risposta senza radicali.
Consigli
- Assicurati di mettere +/- nei posti giusti altrimenti otterrai solo una risposta.
- Anche se conosci la formula della radice quadrata, non può far male esercitarsi a dividere i quadrati o elaborare equazioni quadratiche di tanto in tanto. In questo modo sai per certo di sapere come farlo quando è necessario.
Articoli sull'argomento "Piazza spaccata"
Condividi sui social network:
Simile
Popolare