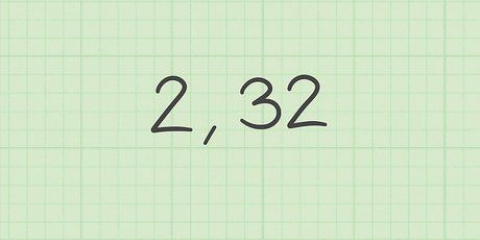Calcolo della Proporzione: 7 Passaggi (con Immagini)

Contenuto

Passi
- Parte 1 di 2: Scrivere un rapporto
- Parte 2 di 2: Uso dei rapporti nei problemi di matematica
Esempi di esercizi
Consigli
Necessità

Proporzioni o rapporti sono espressioni matematiche che confrontano due o più numeri. Le proporzioni possono confrontare quantità e numeri fissi o può essere utilizzato per confrontare parti del tutto. Le proporzioni possono essere calcolate e annotate in diversi modi, ma i principi sono gli stessi per tutti i rapporti. Vedere il passaggio 1 di seguito per iniziare con le proporzioni.

Passi

Parte 1 di 2: Scrivere un rapporto

Immagine titolata Calculate Ratios Step 1

1. Comprendi come vengono utilizzate le proporzioni. Le relazioni si trovano ovunque, nel mondo scientifico oa casa. I rapporti più semplici confrontano solo due valori, ma ovviamente è possibile anche di più.

Un esempio: in una classe con 20 studenti di cui 5 ragazze e 15 ragazzi, possiamo esprimere il numero di ragazze e ragazzi come rapporto.

Immagine titolata Calculate Ratios Step 2

2. Scrivi un rapporto con i due punti. Un modo comune per indicare un rapporto è con i due punti tra i numeri. Se confronti due numeri, scrivilo, ad esempio, come 7 : 13 e se ci sono 3 o più numeri, allora ad esempio come segue 10 : 2 : 23.

Quindi, nella nostra classe, possiamo scrivere il rapporto tra ragazze e ragazzi come segue:5 ragazze: 15 ragazzi. Puoi opzionalmente omettere la designazione, purché ricordi cosa significa il rapporto.

Immagine titolata Calculate Ratios Step 3

3. Un rapporto è uguale a una frazione e può quindi essere semplificato. Lo fai dividendo tutti i termini del rapporto per i comuni divisori, finché non rimangono più comuni divisori. Ma quando lo fai, è importante non dimenticare quali erano i numeri originali del rapporto. Vedi sotto.

Nell`esempio della classe c`erano 5 ragazze e 15 ragazzi. Entrambi i membri del rapporto sono divisibili per 5. Ciò consente di semplificare il rapporto a1 ragazza: 3 ragazzi.

Ma non dobbiamo perdere di vista i numeri originali. Non ci sono 4 ma 20 studenti in totale nella classe. Il rapporto semplificato confronta solo il rapporto tra il numero di maschi e femmine. Ci sono 3 ragazzi per 1 ragazza nel rapporto o frazione, non 3 ragazzi e 1 ragazza nella classe.

Alcune proporzioni non possono essere semplificate. Ad esempio, 3 : 56 non può essere semplificato perché i 2 numeri non hanno fattori uguali: 3 è primo e 56 non è divisibile per 3.

4. Esistono anche metodi alternativi per scrivere le proporzioni. Sebbene i due punti siano forse il modo più semplice per scrivere i rapporti, ci sono altri modi che non influiscono sul rapporto. Vedi sotto:

Le proporzioni possono anche essere visualizzate come "3 sta a 6" o "11 su 4 su 20".

Puoi anche scrivere le proporzioni come una frazione. Spesso l`uso di entrambi i termini crea una certa confusione, ma le frazioni sono proporzioni e viceversa. Quindi puoi anche scrivere un rapporto con una linea di divisione. Ad esempio, il rapporto 3/5 e la frazione 3/5 non differiscono tra loro. Come per l`esempio di classe: c`erano 3 ragazzi per ogni ragazza, un rapporto di 1 : 3, ma come frazione esprime la stessa cosa, ovvero 1/3 del numero totale degli studenti è una ragazza.

Parte 2 di 2: Uso dei rapporti nei problemi di matematica

1. Usa la moltiplicazione o la divisione per cambiare i rapporti senza cambiare il rapporto. Moltiplicare o dividere entrambi i termini di un rapporto per un dato numero produce lo stesso rapporto, ma con numeri maggiori o minori.

Ad esempio, supponiamo che tu sia un insegnante e ti venga chiesto di aumentare la dimensione della classe 5 volte, ma con lo stesso rapporto tra maschi e femmine. Se ci sono 8 ragazze e 11 ragazzi nella classe ora, quanti sono nella nuova classe?Continua a leggere per la soluzione:

8 ragazze e 11 ragazzi, quindi un rapporto di 8 : 11. Questo rapporto indica quindi che, indipendentemente dalla dimensione della classe, ci sono 8 ragazze per 11 ragazzi.
(8 : 11) × 5
(8×5: 11×5)
(40:55). La nuova classe è composta da 40 ragazze e 55 ragazzi - 95 studenti in totale!

Immagine titolata Calculate Ratios Step 4

2. Usa la moltiplicazione incrociata per trovare la variabile sconosciuta, quando lavori con due rapporti equivalenti. Un altro problema noto è quello in cui ti viene chiesto di calcolare l`incognita di un rapporto. La moltiplicazione incrociata rende molto facile risolverlo. Scrivi ogni rapporto come una frazione, rendili uguali e moltiplicali in modo incrociato per risolvere.

Ad esempio, supponiamo di avere un gruppo di studenti di 2 ragazzi e 5 ragazze. Se vogliamo mantenere intatto il rapporto, quanti ragazzi ci sono in un gruppo di 20 ragazze?Per risolvere questo facciamo due rapporti, uno con la variabile sconosciuta: 2 ragazzi : 5 ragazze = x ragazzi : 20 ragazze. In forma di frazione appare così: 2/5 = x/20. Usa la moltiplicazione incrociata per risolvere questo problema. Vedi sotto:

2/5 = x/20

5 × x = 2 × 20

5x = 40

x = 40/5 = 8. Quindi ci sono 20 ragazze e 8 ragazzi.

3. Usa i rapporti per trovare quantità incognite, dove è data un`altra. Se hai a che fare con una variabile che determina la relazione tra più grandezze, di cui 1 o più sono sconosciute, puoi trovare il valore di ciascuna incognita utilizzando una sola grandezza nota. Spesso questi tipi di affermazioni comportano il calcolo delle quantità di ingredienti in una ricetta. Per trovare le incognite, dividi il termine noto del rapporto per la quantità data; condividere dopo ogni termine nel rapporto dalla risposta che ottieni. Un esempio renderà tutto un po` più chiaro:

Supponiamo che la nostra classe stia preparando i biscotti come compito. Se la ricetta dell`impasto è composta da farina, acqua e burro nel rapporto 20 : 8 : 4, e ogni studente riceve 5 tazze di farina; di quanta acqua e burro ha bisogno ogni studente? Per risolvere questo problema, dividere prima il termine del rapporto corrispondente al rapporto noto (20) per la quantità nota (5 tazze). Quindi dividi ogni termine nel rapporto per la risposta che ottieni per trovare l`importo esatto per ciascuno. Vedi sotto:

20 / 5 = 4

20/4 : 8/4 : 4/4

5 : 2 : 1. Così, 5 tazze di farina, 2 tazze d`acqua e 1 tazza di burro.

Esempi di esercizi

I biscotti sono fatti di burro e zucchero in un rapporto di 5:3. Se si utilizzano 7 parti di burro, quanto zucchero è necessario?

Per fare ciò, usa il rapporto sotto forma di frazione. In questo caso lo rendiamo decimale – circa 1,67.
La formula è ora pronta per l`uso. Vogliamo trovare la quantità di zucchero, quindi lasciamo perdere quello che è e calcoliamo la frazione burro/1,67, quindi 7/1,67 = 4,192

La parte che si occupa delle proporzioni è la divisione proporzionale. Quando una quantità totale viene divisa in parti, viene creato un rapporto. Ad esempio: Annemiek, Anna e Anton lavorano tutti nel negozio della madre. Annemiek ha lavorato un`ora, Anna 3 e Anton 6 ore (quindi un rapporto 1:3:6). La madre dà loro un importo totale e chiede loro di dividerlo loro stessi nella giusta proporzione. L`importo totale era di 100 euro. Lo fai sommando le parti del rapporto, in modo da sapere quanto vale ciascuna parte. 1:3:6 diventa quindi 1+3+6=10 quindi $100/10=$10 quindi ora sappiamo che ogni parte del rapporto vale $10... ed è per questo che ognuno riceve uno stipendio di 10 euro l`ora. Ora possiamo usarlo per calcolare ciò che ognuno ha guadagnato. Annemiek riceve 10 euro, Anna 30 euro e Anton 60 euro. Verifica questo sommando tutti gli stipendi, che dovrebbero arrivare a € 100. 10+30+60= 100. Corretta!

Consigli

Semplifica i rapporti usando il pulsante ab/c sulla calcolatrice (questo serve per scrivere frazioni miste e semplificare). Ad esempio, se hai 8:12, esegui il test "8 ab/c 12" = in e ottieni 2/3, e quindi il rapporto 2:3.