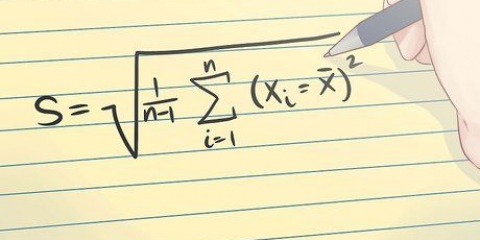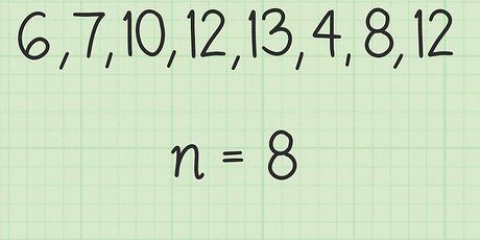Come regola generale, il livello di significatività (o alfa) è spesso impostato su 0,05, il che significa che la probabilità di osservare accidentalmente le differenze presenti nei dati è solo del 5%. Un livello di confidenza più alto (e quindi un valore p più basso) significa che i risultati sono più significativi. Se si desidera che i dati siano più affidabili, impostare il valore p inferiore a 0,01. I valori p inferiori sono comunemente usati nell`industria durante il debug dei prodotti. È molto importante essere in grado di avere grande fiducia che ogni parte funzioni esattamente come dovrebbe. Per la maggior parte degli esperimenti verso un`ipotesi, è accettabile un livello di significatività di 0,05. 
Se non sei sicuro che i tuoi dati siano al di sopra o al di sotto del gruppo di controllo, utilizza un test su due fronti. Consente di verificare la significatività in entrambe le direzioni. Se sai in quale direzione tendono a muoversi i tuoi dati, usa un test a una coda. Nell`esempio fornito, ti aspetti che i voti degli studenti migliorino; ecco perché usi un test a una coda. 
I ricercatori di solito fanno un piccolo studio pilota per informare la loro analisi della forza e per determinare la dimensione del campione necessaria per uno studio più ampio e completo. Se non hai le risorse per fare uno studio pilota complesso, fai delle stime sulle possibili medie sulla base della lettura della letteratura e degli studi che altre persone potrebbero aver fatto. Questo ti darà un buon punto di partenza per iniziare con la dimensione del campione. 

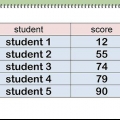
Ad esempio, per trovare il voto medio del gruppo che ha letto il materiale prima della lezione, diamo un`occhiata ad alcuni dati. Per semplicità utilizziamo un set di dati di 5 punti: 90, 91, 85, 83 e 94. Somma tutti i dati insieme: 90 + 91 + 85 + 83 + 94 = 443. Dividi la somma per il numero di dati, N = 5:443 / 5 = 88,6. Il voto medio di questo gruppo è 88,6. 
(90–88,6), (91–88,6), (85–88,6), (83–88,6) e (94–88,6). I numeri calcolati sono ora 1,4, 2,4, -3,6, -5,6 e 5,4. 
Nel nostro esempio stiamo ora lavorando con 1.96 5.76, 12.96, 31.36 e 29.16. Sommando questi quadrati si ottiene: 1,96 + 5,76 + 12,96 + 31,36 + 29,16 = 81,2. 
Sottrai: N – 1 = 5 – 1 = 4 Parte: 81.2/4 = 20.3 
Nel nostro esempio, la deviazione standard dei voti finali degli studenti che hanno letto il materiale prima della lezione è: s = √20,3 = 4,51. 

µ1 è la media del primo gruppo. µ2 è la media del secondo gruppo. SD è la varianza tra i campioni. Usa la media più grande come µ1, quindi non hai un valore negativo per t. Nel nostro esempio, supponiamo che la media campionaria per il Gruppo 2 (quelli che non hanno letto) fosse 80. Il punteggio t è quindi: t = (µ1 – µ2)/SD = (88,6 – 80)/3,29 = 2,61. 

con 8 d.F. e un t-score di 2,61, il p-value per un test a una coda è compreso tra 0,01 e 0,025. Poiché il nostro livello di significatività impostato è inferiore o uguale a 0,05, i nostri dati sono statisticamente significativi. Con questi dati, rifiutiamo l`ipotesi nulla e accettiamo l`ipotesi alternativa: gli studenti che leggono il materiale prima della lezione ottengono voti finali migliori. 
Valutare il significato statistico
Contenuto
La verifica delle ipotesi è supportata dall`analisi statistica. La significatività statistica è calcolata da un p-value, che indica la probabilità del risultato osservato, dato che una certa affermazione (l`ipotesi nulla) è soddisfatta. Se questo valore p è inferiore al livello di significatività dichiarato (solitamente 0,05), lo sperimentatore può presumere che l`ipotesi nulla sia falsa e accettare l`ipotesi alternativa. Utilizzando un semplice t-test, puoi calcolare un valore p e confrontare la significatività tra due diversi gruppi di un set di dati.
Passi
Parte 1 di 3: Impostazione dell`esperimento

1. Definisci la tua ipotesi. Il primo passo per valutare la significatività statistica è definire la domanda a cui rispondere e formulare la propria ipotesi. L`ipotesi è un`affermazione sui tuoi dati sperimentali e sulle differenze che possono esistere nella popolazione. In ogni esperimento c`è sia un`ipotesi nulla che un`ipotesi alternativa. In generale, confronterai due gruppi per vedere se sono uguali o diversi.
- L`ipotesi nulla (H0) in genere afferma che non vi è alcuna differenza tra i due insiemi di dati. Ad esempio: gli studenti che hanno letto il materiale prima della lezione non ottengono voti finali migliori.
- L`ipotesi alternativa (Hun) è l`opposto dell`ipotesi nulla ed è l`affermazione che stai cercando di supportare con i tuoi dati sperimentali. Ad esempio: gli studenti che hanno letto il materiale prima della lezione ottengono voti finali migliori.

2. Imposta il livello di significatività per determinare quanto insoliti devono essere i tuoi dati prima che possano essere considerati significativi. Il livello di significatività (chiamato anche alfa) è la soglia impostata per determinare la significatività. Se il p-value è inferiore o uguale al livello di significatività impostato, i dati possono essere considerati statisticamente significativi.

3. Decidi di utilizzare un test a una o due code. Una delle ipotesi fatte da un t-test è che i dati siano normalmente distribuiti. Una normale distribuzione dei dati forma una curva a campana con la maggior parte dei dati del test che cadono nel mezzo. Il t-test è un test matematico per vedere se i dati cadono al di fuori della distribuzione normale (sopra o sotto), nelle "code" della curva.

4. Determinare la dimensione del campione con un`analisi della forza. La potenza di un test è la probabilità che il risultato atteso venga osservato, data una specifica dimensione del campione. La soglia comune per la forza (o β) è 80%. Un`analisi della potenza può diventare un po` complicata senza alcuni dati preliminari perché sono necessarie alcune informazioni sui valori medi previsti tra ciascun gruppo e le loro deviazioni standard. Utilizza un calcolatore di analisi della forza online per determinare la dimensione ottimale del campione per i tuoi dati.
Parte 2 di 3: Calcolo della deviazione standard

1. Trova la formula per la deviazione standard. La deviazione standard è una misura della diffusione dei tuoi dati. Fornisce informazioni sulla somiglianza di ciascun punto dati all`interno del campione. A prima vista, l`equazione può sembrare un po` complicata, ma i seguenti passaggi ti guideranno attraverso il calcolo. La formula è: s = √∑((xio – µ)/(N – 1)).
- s è la deviazione standard.
- ∑ indica che è necessario sommare tutti i valori del campione raccolti.
- Xio rappresenta ogni singolo valore dei tuoi dati.
- µ è la media (o il centro) dei tuoi dati per ciascun gruppo.
- N è il totale del campione.

2. Calcola la media dei dati del test in ciascun gruppo. Per calcolare la deviazione standard, devi prima calcolare la media dei dati del test nei singoli gruppi. La media è indicata dalla lettera greca mu o µ. Per fare ciò, somma ogni dato e poi dividilo per il numero totale di dati.

3. Sottrarre ogni metrica dalla media. La parte successiva del calcolo include la parte (xio – µ) dell`equazione. Sottrarre ogni dato dalla media appena calcolata. Nel nostro esempio, ti ritroverai con cinque sottrazioni.

4. Quadra ciascuno di questi numeri e sommali. Ciascuno dei nuovi numeri appena calcolati sarà ora al quadrato. Questo passaggio crea anche segni negativi. Se hai un segno meno dopo questo passaggio o alla fine del calcolo, potresti aver dimenticato questo passaggio.

5. Dividilo per la dimensione del campione totale, meno 1. La formula divide per N-1, perché corregge il fatto che non hai ancora contato un`intera popolazione; prendi un campione dalla popolazione di tutti gli studenti per fare una stima.

6. Prendi la radice quadrata. Dopo aver diviso per il numero di dati meno uno, calcola la radice quadrata di quest`ultimo numero. Questo è l`ultimo passaggio per il calcolo della deviazione standard. Ci sono programmi statistici che possono fare questo calcolo per te, dopo aver inserito i dati grezzi.
Parte 3 di 3: Determinare il significato

1. Calcola la differenza tra i due gruppi del campione. Fino a questo punto l`esempio ha coperto solo uno dei gruppi campione. Se vuoi confrontare due gruppi, avrai ovviamente i dati di entrambi i gruppi. Calcolare la deviazione standard del secondo gruppo di dati di prova e utilizzarla per calcolare la differenza tra i due gruppi sperimentali. La formula della varianza è sD = √((s1/N1) + (s2/N2)).
- SD è la varianza tra i tuoi gruppi.
- S1 è la deviazione standard del gruppo 1 e N1 è la dimensione del campione del gruppo 1.
- S2 è la deviazione standard del gruppo 2 e N2 è la dimensione del campione del gruppo 2.
- Per il bene del nostro esempio, diciamo che i dati del Gruppo 2 (studenti che non avevano letto prima della lezione) avevano una dimensione del campione di 5 e una deviazione standard di 5,81. La varianza è:
- SD = √((s1)/N1) + ((s2)/N2))
- SD = √(((4.51)/5) + ((5.81)/5)) = √((20.34/5) + (33.76/5)) = √(4.07 + 6.75) = √10.82 = 3.29.

2. Calcola il punteggio t dei tuoi dati. Con un punteggio t puoi convertire i dati in un modulo che puoi confrontare con altri dati. Con t-score è possibile eseguire un t-test, per calcolare la probabilità che due gruppi differiscano significativamente l`uno dall`altro. La formula per un punteggio t è: t = (µ1 – µ2)/SD.

3. Determina il grado di libertà del tuo campione. Quando si utilizza il punteggio t, i gradi di libertà vengono determinati utilizzando la dimensione del campione. Somma il numero di dati del test di ciascun gruppo, quindi dividi per due. Nel nostro esempio, i gradi di libertà; d.F.) 8, perché c`erano cinque dati nel primo gruppo e cinque nel secondo gruppo ((5 + 5) – 2 = 8).

4. Utilizzare una tabella t per valutare la significatività. Una tabella con i punteggi t e il numero di gradi di libertà può essere trovata in un libro di statistiche standard o online. Guarda la riga dei gradi di libertà per i tuoi dati e trova il valore p che corrisponde al tuo punteggio t.

5. Considera uno studio di follow-up. Molti ricercatori fanno un piccolo studio pilota con poche misurazioni per capire come impostare uno studio più ampio. Un altro studio, con più misurazioni, ti aiuterà ad aumentare la tua fiducia nella tua conclusione.
Consigli
- La statistica è un campo vasto e complicato. Partecipa a una classe di scuola superiore o di istruzione superiore sull`inferenza statistica per comprendere meglio la significatività statistica.
Avvertenze
- Questa analisi è specifica per un t-test per testare le differenze tra due popolazioni normalmente distribuite. Potrebbe essere necessario un test statistico diverso a seconda della complessità della raccolta dei dati.
Articoli sull'argomento "Valutare il significato statistico"
Condividi sui social network:
Simile
Popolare