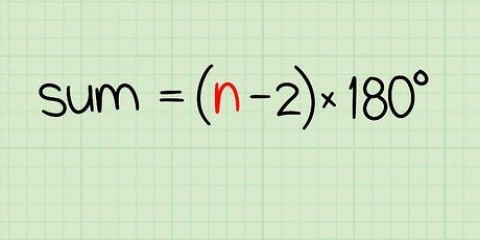Ad esempio, se vuoi calcolare la somma delle serie 10, 15, 20, 25, 30, allora  , perché ci sono cinque numeri nella sequenza.
, perché ci sono cinque numeri nella sequenza. 
Ad esempio, nella sequenza 10, 15, 20, 25, 30  , e
, e  .
. 

Ad esempio, se nella sequenza sono presenti cinque numeri, dove 10 è il primo numero e 30 è l`ultimo numero, la formula sarà simile alla seguente:  .
. 
Ad esempio:



Ad esempio:


Quindi la somma delle serie (10, 15, 20, 25, 30) è uguale a 100. 

Determina il numero di numeri ( ) nella serie. Poiché inizi con tre, finisci con 24 e aggiungi sette ogni volta, la sequenza di numeri è 3, 10, 17, 24. (Il fattore di differenza è la differenza tra ogni numero della serie.) Ciò significa che
) nella serie. Poiché inizi con tre, finisci con 24 e aggiungi sette ogni volta, la sequenza di numeri è 3, 10, 17, 24. (Il fattore di differenza è la differenza tra ogni numero della serie.) Ciò significa che 
Determina il primo ( ) e ultimo (
) e ultimo ( ) numero nella sequenza. Poiché la sequenza è da 3 a 24,
) numero nella sequenza. Poiché la sequenza è da 3 a 24,  e
e  .
. Trova la media di  e
e  :
:  .
. Moltiplica la media per  :
:  .
. 
Determina il numero di termini ( ) nella serie. Perché Mara risparmia per 52 settimane, (1 anno),
) nella serie. Perché Mara risparmia per 52 settimane, (1 anno),  .
. Determina il primo ( ) e ultimo (
) e ultimo ( ) numero nella sequenza. Il primo importo che risparmia è di cinque euro, quindi
) numero nella sequenza. Il primo importo che risparmia è di cinque euro, quindi  . Per calcolare l`importo totale risparmiato nell`ultima settimana dell`anno, calcoliamo
. Per calcolare l`importo totale risparmiato nell`ultima settimana dell`anno, calcoliamo  . così
. così  .
. Determina la media di  e
e  :
:  .
. Moltiplica la media per  :
:  . Così ha risparmiato 6890 euro a fine anno.
. Così ha risparmiato 6890 euro a fine anno.
Trovare la somma di una sequenza aritmetica
Contenuto
Una sequenza aritmetica è una sequenza di numeri in cui ogni numero aumenta di un valore costante. Per la somma di una sequenza aritmetica, puoi sommare tutti i numeri insieme. Tuttavia, questo non è realmente pratico quando la sequenza contiene un gran numero di termini. Invece, puoi trovare rapidamente la somma di ogni sequenza aritmetica moltiplicando la media del primo e dell`ultimo numero per il numero di termini nella sequenza.
Passi
Parte 1 di 3: Analizzare la sequenza

1. Assicurati di avere una sequenza aritmetica. Una sequenza aritmetica è un elenco ordinato di numeri, in cui il cambiamento dei numeri è costante. Questo metodo funziona solo se il tuo insieme di numeri è una sequenza aritmetica.
- Per determinare se hai a che fare con una sequenza aritmetica, trova la differenza tra la prima o l`ultima coppia di numeri. Assicurati che la differenza sia sempre la stessa.
- Ad esempio, la sequenza dei numeri 10, 15, 20, 25, 30 è una sequenza aritmetica, perché la differenza tra ogni numero è costantemente cinque.

2. Determina il numero di termini nella tua sequenza. Ogni numero è un termine. Se viene menzionato un solo numero, puoi contarli. Se conosci il primo numero, l`ultimo numero e il fattore di differenza (la differenza tra ogni numero), puoi utilizzare una formula per determinare il numero di numeri. Questo numero è rappresentato dalla variabile  .
.
 .
. , perché ci sono cinque numeri nella sequenza.
, perché ci sono cinque numeri nella sequenza.
3. Trova il primo e l`ultimo numero della sequenza. Devi conoscere entrambi i numeri per calcolare la somma della sequenza aritmetica. Spesso il primo numero sarà uno, ma non sempre. Imposta la variabile  uguale al primo numero della sequenza, e
uguale al primo numero della sequenza, e  uguale all`ultimo numero della sequenza.
uguale all`ultimo numero della sequenza.
 uguale al primo numero della sequenza, e
uguale al primo numero della sequenza, e  uguale all`ultimo numero della sequenza.
uguale all`ultimo numero della sequenza. , e
, e  .
.Parte 2 di 3: Calcola la somma

1. Scrivi la formula per trovare la somma di una sequenza aritmetica. La formula è  , per cui
, per cui  è uguale alla somma della serie.
è uguale alla somma della serie.
 , per cui
, per cui  è uguale alla somma della serie.
è uguale alla somma della serie. - Si noti che questa formula indica che la somma della sequenza aritmetica è uguale alla media del primo e dell`ultimo numero moltiplicata per il numero dei numeri.

2. Inserisci i valori n  ,
, un 1  e
e un n  nella formula in. Assicurati di sostituire correttamente.
nella formula in. Assicurati di sostituire correttamente.
 ,
,  e
e  nella formula in. Assicurati di sostituire correttamente.
nella formula in. Assicurati di sostituire correttamente. .
.
3. Calcola la media del primo e del secondo numero. Lo fai sommando i due numeri e dividendo per due.



4. Moltiplica la media per il numero di numeri della serie. Questo ti dà la somma della sequenza aritmetica.


Quindi la somma delle serie (10, 15, 20, 25, 30) è uguale a 100.
Parte 3 di 3: Completamento dei problemi di esempio

1. Trova la somma dei numeri da 1 a 500. Includere tutti gli interi consecutivi nel calcolo.
- Determina il numero di termini (
) nella serie. Poiché stai contando tutti i numeri interi consecutivi fino a 500 inclusi,
.
- Determina il primo (
) e ultimo (
) numero nella sequenza. Poiché assumiamo la serie da 1 a 500, vale
e
.
- Trova la media di
e
:
.
- Moltiplica la media per
:
.

2. Trova la somma della sequenza aritmetica indicata. Il primo numero della sequenza è tre. L`ultimo numero della sequenza è 24. Il fattore di differenza è sette.
 ) nella serie. Poiché inizi con tre, finisci con 24 e aggiungi sette ogni volta, la sequenza di numeri è 3, 10, 17, 24. (Il fattore di differenza è la differenza tra ogni numero della serie.) Ciò significa che
) nella serie. Poiché inizi con tre, finisci con 24 e aggiungi sette ogni volta, la sequenza di numeri è 3, 10, 17, 24. (Il fattore di differenza è la differenza tra ogni numero della serie.) Ciò significa che 
 ) e ultimo (
) e ultimo ( ) numero nella sequenza. Poiché la sequenza è da 3 a 24,
) numero nella sequenza. Poiché la sequenza è da 3 a 24,  e
e  .
. e
e  :
:  .
. :
:  .
.
3. Risolvi il seguente problema. Mara risparmia 5 euro la prima settimana dell`anno. Per il resto dell`anno aumenta i suoi risparmi di 5 euro ogni settimana. Quanti soldi ha risparmiato Mara alla fine dell`anno?
 ) nella serie. Perché Mara risparmia per 52 settimane, (1 anno),
) nella serie. Perché Mara risparmia per 52 settimane, (1 anno),  .
. ) e ultimo (
) e ultimo ( ) numero nella sequenza. Il primo importo che risparmia è di cinque euro, quindi
) numero nella sequenza. Il primo importo che risparmia è di cinque euro, quindi  . Per calcolare l`importo totale risparmiato nell`ultima settimana dell`anno, calcoliamo
. Per calcolare l`importo totale risparmiato nell`ultima settimana dell`anno, calcoliamo  . così
. così  .
. e
e  :
:  .
. :
:  . Così ha risparmiato 6890 euro a fine anno.
. Così ha risparmiato 6890 euro a fine anno.Articoli sull'argomento "Trovare la somma di una sequenza aritmetica"
Condividi sui social network:
Popolare