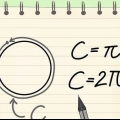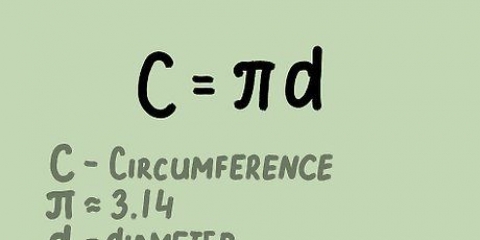Memorizzare il Cerchio Unitario: 14 Passaggi (con Immagini)

Contenuto

Passi
- Parte 1 di 2: Ricorda i radianti
- Parte 2 di 2: ricorda le coordinate xey (coseno, seno)
Consigli

Imparare il cerchio unitario ti aiuterà non solo con la trigonometria e la geometria, ma anche con il calcolo differenziale e integrale. Può sembrare un sacco di memorizzazione, ma una volta capito come funziona, puoi iniziare con alcuni numeri dal cerchio delle unità e capire rapidamente il resto.

Passi

Parte 1 di 2: Ricorda i radianti

Immagine titolata Memorize the Unit Circle Step 1

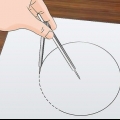
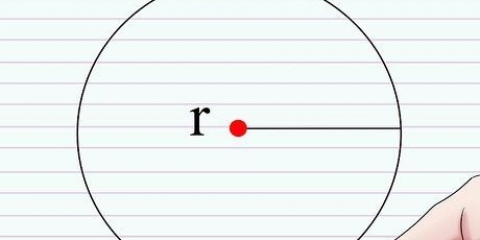
1. Disegna due linee perpendicolari. Posiziona un compasso su un grande foglio di carta. Disegna una linea verticale e una orizzontale. Questi dovrebbero intersecare vicino al centro della pagina. Questi sono l`asse x e l`asse y del grafico.

Immagine titolata Memorize the Unit Circle Step 2

2. Disegna un cerchio. Usando un compasso, disegna un grande cerchio centrato all`intersezione delle due linee.

Immagine titolata Memorize the Unit Circle Step 3

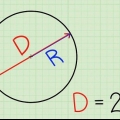
3. Comprendi i radianti. Un radiante è una misura dell`angolo. È principalmente definito in modo tale che una persona che cammina intorno a un cerchio con a Ray di 1 unità si muove di un angolo di un radiante dopo aver percorso 1 unità lungo il perimetro. Nel passaggio successivo, indicheremo i quattro punti di coordinate con il valore in radianti. Se ricordi la formula per la relazione tra la circonferenza di un cerchio e il suo raggio, puoi elaborarla rapidamente, ma anche se non la ricordi.

Le misure in radianti della circonferenza unitaria presuppongono sempre che si parte dal punto (0, 1). Per chiarire a quale punto ci riferiamo, descriviamo il cerchio come una rosa dei venti:

Immagine titolata Memorize the Unit Circle Step 4

4. Ricorda che la circonferenza del cerchio è 2π. La circonferenza di un cerchio è uguale a 2πR, per cui R sta per il raggio (il raggio). Poiché la circonferenza unitaria ha raggio 1, possiamo semplificare la circonferenza a 2π. Il valore in radianti di qualsiasi punto della circonferenza può essere trovato semplicemente dividendo 2π per quella parte del cerchio che avevi. Questo è molto più facile che memorizzare ogni singolo valore sul cerchio.

Immagine titolata Memorize the Unit Circle Step 5

5. Indica i quattro punti sugli assi xey. Tutto quello che devi fare è dividere 2π in quarti:

"Est" è il punto di partenza, quindi è così 0 aveva radianti.

`Nord` = un quarto della circonferenza del cerchio = /₄ = /₂ radianti.

`Ovest` = metà del cerchio = /₂ = π radianti.

`Sud` = tre quarti del cerchio = 2π * ¾ = /₂ radianti.

Se percorri l`intero perimetro, torni al punto di partenza. Puoi indicarlo come 2π o 0.

Immagine titolata Memorize the Unit Circle Step 6

6. Dividi il cerchio in otto pezzi. Ora traccia una linea diagonale attraverso ogni quadrante, perfettamente attraverso il centro. Ancora una volta, usa la divisione per trovare il valore in radianti:

/₄

(π/2, π, 3π/2 e 2π sono già stati indicati.)

Immagine titolata Memorize the Unit Circle Step 7

7. Dividi il cerchio in sei segmenti. Ora disegna linee aggiuntive che dividono il cerchio in sei segmenti. (Puoi usare un goniometro per questo, partendo dall`asse x positivo, dove ogni segmento misura 60 gradi). Puoi usare lo stesso approccio di cui sopra per assicurarti che un sesto di un cerchio sia uguale a /₆ = /₃ radianti. Utilizzare questa etichetta per i seguenti punti sul perimetro (uno in ogni quadrante):

/₃

(π e 2π sono già indicati)

Immagine titolata Memorize the Unit Circle Step 8

8. Disegna i dodicesimi in esso. Gli ultimi punti segnati sulla maggior parte dei cerchi unitari indicano incrementi di un dodicesimo della circonferenza. Solo quattro di questi non sono stati ancora dichiarati:

/₆

Parte 2 di 2: ricorda le coordinate xey (coseno, seno)

Immagine titolata Memorize the Unit Circle Step 9

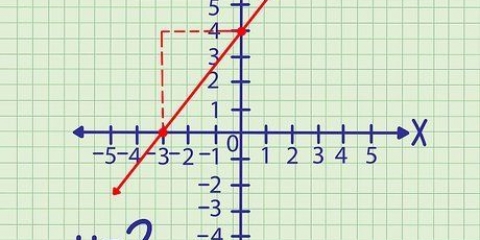
1. Comprendere coseno e seno. Il cerchio unitario è particolarmente utile per i calcoli trigonometrici con angoli retti. Qualsiasi coordinata x di un punto sulla circonferenza è uguale a cos(θ) e qualsiasi coordinata y è uguale a sin(θ), dove θ è il valore dell`angolo.

Se trovi difficile ricordare, pensa a (cos, sin) `perché il seno viene per ultimo`.
Puoi dedurlo usando i triangoli rettangoli e la definizione di queste funzioni - ricorda `soscastoa`?

Immagine titolata Memorize the Unit Circle Step 10

2. Annota le coordinate in quattro punti del cerchio. Un "cerchio unitario" è semplicemente un cerchio con un raggio esattamente di un`unità. Usali per trovare le coordinate xey dei quattro punti sul cerchio in cui si interseca con un asse. (Chiamiamo questi `Est`, `Nord`, ecc. per facilità di lettura, ma questi non sono nomi ufficiali).

Le coordinate di `Est` sono (1, 0).

Le coordinate di `Nord` sono (0, 1).

Le coordinate di `Ovest` sono (-1, 0).

Le coordinate di `Sud` sono (0, -1).

Funziona proprio come un normale grafico. Dovresti essere in grado di trovare queste coordinate da solo, senza doverle memorizzare.

Immagine titolata Memorize the Unit Circle Step 11

3. Memorizza le coordinate del primo quadrante. Il primo quadrante è il quarto in alto a destra del cerchio, dove entrambi i valori x come la y-i valori sono positivi. Queste sono le uniche coordinate che devi ricordare:

Sopra /₆, sono le coordinate ( $\frac{\sqrt{3}}{2}, \frac{1}{2}$ ${frac{{sqrt{3}}}{2}},{frac{1}{2}}$ ).

Sopra /₄, sono le coordinate ( $\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}$ ${frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ).

Sopra /₃, sono le coordinate ( $\frac{1}{2}, \frac{\sqrt{3}}{2}$ ${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ).

Nota che ci sono solo tre contatori. Ti stai muovendo in una direzione positiva (da sinistra a destra per il valori x, dal basso verso l`alto per il valori y), allora la sequenza è la seguente: 1 → √2 → √3.

Immagine titolata Memorize the Unit Circle Step 12

4. Disegna linee rette per riempire le altre coordinate. Se riesci a tracciare una linea perfettamente verticale o perfettamente orizzontale tra due punti, allora hanno lo stesso valore assoluto delle coordinate x e y. In altre parole, puoi tracciare una linea da un punto nei primi quadranti, scrivere le stesse coordinate nel punto in cui atterri e lasciare spazio a destra per il segno (+ o -).

Ad esempio, puoi tracciare una linea orizzontale tra /₃ e /₃. Poiché le coordinate del primo punto (

\frac{1}{2}, \frac{\sqrt{3}}{2}

${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ), le coordinate del secondo punto (?

\frac{1}{2}, ? \frac{\sqrt{3}}{2}

${frac{1}{2}},?{frac{{sqrt{3}}}{2}}$ ), per cui `?` rappresenta un segno più o meno (+ o -).

Ecco un modo più veloce: controlla il denominatore dei radianti. Tutti i punti che terminano con /3 hanno le stesse coordinate assolute, proprio come tutti i punti che terminano con /4 e tutti i punti che terminano con /6.

Immagine titolata Memorize the Unit Circle Step 13

5. Usa la simmetria per scoprire se il segno è positivo o negativo. Esistono diversi modi per ricordare dove posizionare i segni meno sul cerchio dell`unità:

Pensa alle regole fondamentali per i grafici. Sopra il X-asse i punti sono positivi, sotto di esso negativi. A sinistra del y è negativo, giusto è positivo.

Inizia dal quadrante 1 e traccia linee verso altri punti. Se la linea de y-l`asse incrocia il valore y cambierà segno. Se la linea de X-l`asse si incrocia, quindi il valore x cambia segno.

Impara "All Students Test Calculus" (ASTC), in senso antiorario. Il quadrante 1 ha unsolo valori positivi, il quadrante 2 ha solo valori positivi Sinus, il quadrante 3 ha solo valori positivi Tangens e il quadrante 4 ha solo valori positivi Cvalori di osino.

Indipendentemente dal metodo scelto, i segni sono (+, +) per il quadrante 1, (-, +) per il quadrante 2, (-, -) per il quadrante 3 e (+,-) per il quadrante 4.

Immagine titolata Memorize the Unit Circle Step 14

6. Controlla il tuo lavoro. Ecco l`elenco completo dei valori delle coordinate per ogni punto etichettato sul cerchio (senza contare i quattro punti sugli assi), in senso orario. Ricorda, dovresti riuscire a trovare tutti questi valori semplicemente memorizzando i punti del quadrante 1:

Quadrante 1: (

\frac{\sqrt{3}}{2}, \frac{1}{2}

${frac{{sqrt{3}}}{2}},{frac{1}{2}}$ ); (

\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}

${frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ); (

\frac{1}{2}, \frac{\sqrt{3}}{2}

${frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ).

Quadrante 2: (

- \frac{1}{2}, \frac{\sqrt{3}}{2}

$-{frac{1}{2}},{frac{{sqrt{3}}}{2}}$ ); (

- \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}

$-{frac{{sqrt{2}}}{2}},{frac{{sqrt{2}}}{2}}$ ); (

- \frac{\sqrt{3}}{2}, \frac{1}{2}

$-{frac{{sqrt{3}}}{2}},{frac{1}{2}}$ )

Quadrante 3: (

- \frac{\sqrt{3}}{2}, - \frac{1}{2}

$-{frac{{sqrt{3}}}{2}},-{frac{1}{2}}$ ); (

- \frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2}

$-{frac{{sqrt{2}}}{2}},-{frac{{sqrt{2}}}{2}}$ ); (

- \frac{1}{2}, - \frac{\sqrt{3}}{2}

$-{frac{1}{2}},-{frac{{sqrt{3}}}{2}}$ )

Quadrante 4: (

\frac{1}{2}, - \frac{\sqrt{3}}{2}

${frac{1}{2}},-{frac{{sqrt{3}}}{2}}$ ); (

\frac{\sqrt{2}}{2}, - \frac{\sqrt{2}}{2}

${frac{{sqrt{2}}}{2}},-{frac{{sqrt{2}}}{2}}$ ); (

\frac{\sqrt{3}}{2}, - \frac{1}{2}

${frac{{sqrt{3}}}{2}},-{frac{1}{2}}$ )

Consigli

Se hai una prova o una prova sul cerchio dell`unità, prima disegna il cerchio su carta straccia in modo da poterlo utilizzare come riferimento per ogni problema.
Il processo sarà notevolmente più veloce se ti eserciti molto. In futuro, potresti aver bisogno di vedere solo gli assi xey per ricordare tutto, oppure potresti non aver più bisogno di un grafico.