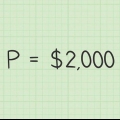Come Calcolare l'Interesse Composto: 15 Passaggi (con Immagini)

Contenuto

Passi
Consigli

L`interesse composto differisce dall`interesse semplice in quanto il rendimento dell`interesse è calcolato sia sull`investimento originale (capitale) che sull`interesse maturato fino ad oggi, piuttosto che solo sul capitale. Ecco perché i conti con interessi composti crescono più velocemente dei conti con interessi semplici. Inoltre, il valore crescerà ancora più velocemente se l`interesse viene composto più volte all`anno. Gli interessi composti (chiamati anche interessi) possono essere trovati con vari prodotti di investimento e anche come interessi su determinati tipi di prestiti, come i debiti delle carte di credito. Con le giuste equazioni, calcolare quanto crescerà un importo attraverso l`interesse composto è molto semplice.

Passi

Parte 1 di 3: Calcolo dell`interesse composto annuo

Immagine titolata Calculate Compound Interest Step 1

1. Definire l`interesse composto annuo. Il tasso di interesse indicato sul prospetto di investimento o sul contratto di prestito è su base annuale. Se prendi un prestito auto, ad esempio, al 6% di interesse, paghi il 6% di interesse all`anno. Un interesse composto di fine anno è il calcolo dell`interesse composto più semplice.

L`interesse composto su un debito può essere calcolato annualmente, mensilmente o anche giornalmente.
Più spesso il tuo debito viene aggravato, più velocemente accumuleranno i tuoi interessi.
Puoi guardare all`interesse composto dal punto di vista di un investitore o di un debitore. L`interesse composto calcolato di frequente significa che il reddito da interessi degli investitori crescerà a un ritmo più rapido. Significa anche che il debitore dovrà più interessi su un debito in sospeso.
Ad esempio, gli interessi possono essere calcolati annualmente su un conto di risparmio, mentre gli interessi su un prestito lampo possono essere calcolati mensilmente o anche settimanalmente.

Immagine titolata Calculate Compound Interest Step 2

2. Calcola l`interesse annuo composto per l`anno 1. Supponi di possedere un titolo di Stato da € 1.000, ad un tasso di interesse del 6%. I titoli di stato pagano dividendi ogni anno in base agli interessi e al valore attuale.

L`interesse per l`anno 1 sarà quindi di € 60 (€ 1.000 x 6%).

Per calcolare l`interesse per l`anno 2, è necessario aggiungere il capitale originale all`interesse totale fino ad oggi. In questo caso il capitale dell`anno 2 è pari a 1 euro.060 (€1.000 + 60€). Il valore dell`obbligazione è quindi di 1€.060 e in base a questo valore si calcolano gli interessi da pagare.

Immagine titolata Calculate Compound Interest Step 3

3. Calcola l`interesse composto per gli anni successivi. Per vedere il maggiore impatto dell`interesse composto, calcola l`interesse per gli anni successivi. Il principale continua a crescere di anno in anno.

Moltiplica il capitale dell`anno 2 per il tasso di interesse dell`obbligazione ($1.060 X 6% = 63,60 €). L`interesse ottenuto è superiore di € 3,60 (€ 63,60 - € 60,00). Questo perché il capitale è aumentato da $ 1.000 a 1 €.060.

Per l`anno 3, il capitale è di € 1.123,60 (€1.060 + 63,60 €). L`interesse per l`anno 3 è di € 67,42. Tale importo viene aggiunto al capitale per il calcolo dell`anno 4.

Più a lungo è in essere un debito, maggiore è l`impatto dell`interesse composto. In sospeso significa che il debito deve ancora essere pagato dal debitore.

Senza l`interesse composto, l`interesse guadagnato nell`anno 2 sarebbe di $ 60 (€ 1.000 X 6%). In effetti, ogni anno l`interesse sarebbe di $ 60 se avessi un interesse composto. Questo è noto come interesse semplice.

Immagine titolata Calculate Compound Interest Step 4

4. Crea un documento Excel per il calcolo dell`interesse composto. Può essere utile visualizzare l`interesse composto creando un semplice modello Excel della crescita del tuo investimento. Inizia aprendo un documento ed etichetta la cella in alto nelle colonne A, B e C rispettivamente come "Anno", "Valore" e "Interessi guadagnati".

Digitare gli anni (0-5) nelle celle da A2 a A7.

Digitare il principale nella cella B2. Supponiamo che tu abbia iniziato con 1€.000. Digitare 1000.

Nella cella B3, digita `= B2 *1,06` e premi Invio. Ciò significa che il tuo interesse viene composto annualmente con un interesse del 6% (0,06). Fare clic sull`angolo inferiore destro della cella B3 e trascinare la formula nella cella B7. I numeri sono ora compilati correttamente.

Metti uno 0 nella cella C2. Nella cella C3 digita `=B3-B2` e premi Invio. Questo dà la differenza tra i valori nelle celle B3 e B2, che rappresenta l`interesse. Fare clic sull`angolo inferiore destro della cella C3 e trascinare la formula nella cella C7. I valori dovrebbero essere compilati automaticamente.

Ripetere questa procedura per tutti gli anni che si desidera tenere traccia. Puoi anche modificare facilmente i valori di capitale e tasso di interesse modificando le formule utilizzate e il contenuto della cella.

Parte 2 di 3: Calcolo dell`interesse composto sugli investimenti

Immagine titolata Calculate Compound Interest Step 5

1. Impara la formula dell`interesse composto. La formula dell`interesse composto calcola il valore futuro dell`investimento dopo un certo numero di anni. La formula stessa è la seguente:

F V = P (1 + \frac{io}{C})^{n * C}

$FV=P(1+{frac{i}{c}})^{{n*c}}$ Le variabili all`interno dell`equazione sono definite come segue:

`FV` è il valore futuro. Questo è il risultato del calcolo.
`P` è il tuo principale.
`i` è il tasso di interesse annuo.
`c` è il tasso di interesse composto (la frequenza con cui l`interesse composto viene calcolato annualmente).
`n` è il numero di anni da calcolare.

Immagine titolata Calculate Compound Interest Step 6

2. Raccogli le variabili per la formula dell`interesse composto. Se gli interessi vengono calcolati più spesso di un anno, è difficile calcolare manualmente la formula. È possibile utilizzare una formula di interesse composto per qualsiasi calcolo. Per utilizzare la formula, sono necessarie le seguenti informazioni:

Determinare l`importo principale dell`investimento. Questo è l`importo originale del tuo investimento. Questo può essere quanto hai depositato sul tuo conto o il prezzo originale dell`obbligazione. Ad esempio, supponiamo che il tuo capitale in un conto di investimento sia di € 5.000 è.

Trova il tasso di interesse dell`investimento. Il tasso di interesse deve essere un importo annuo, espresso come percentuale dell`importo capitale. Ad esempio, un tasso di interesse del 3,45% sul capitale di 5 euro.000.

Durante il calcolo, il tasso di interesse deve essere inserito come decimale. Convertilo dividendo il tasso di interesse per 100. In questo esempio diventa 3,45/100 = 0,0345.

Devi anche sapere con quale frequenza viene composto l`interesse. Gli interessi sono solitamente composti annualmente, mensilmente o giornalmente. Supponiamo, ad esempio, che si tratti di interessi mensili. Ciò significa che il tuo tasso di interesse ("c") deve essere inserito come 12.

Determina in quale periodo vuoi calcolare. Questo potrebbe essere un obiettivo di crescita annuale, ad esempio 5 o 10 anni, o la scadenza dell`obbligazione. La data di scadenza di un`obbligazione è la data in cui il capitale dell`investimento deve essere rimborsato. Ad esempio, stiamo usando due anni qui, quindi inserisci un 2.

Immagine titolata Calculate Compound Interest Step 7

3. Usa la formula. Sostituisci le tue variabili nei posti giusti. Si prega di ricontrollare per assicurarsi di averli inseriti correttamente. In particolare, assicurati di aver inserito l`interesse in forma decimale e di aver utilizzato il valore corretto per `c` (tasso di interesse).

L`esempio di investimento viene quindi inserito come segue:

F V = 5000 (1 + 0, 0345 12)^{2 * 12}

$FV=5000(1+{frac{0.0345}{12}})^{{2*12}}$

Calcola separatamente l`esponente e la parte della formula tra parentesi. Questo è un concetto dalla matematica chiamato "ordine delle operazioni". Puoi leggere articoli sull`ordine delle operazioni su wikiHow.

Immagine titolata Calculate Compound Interest Step 8

4. Completa i calcoli matematici nella formula. Semplifica il problema risolvendo prima i termini tra parentesi, iniziando con la frazione.

Per prima cosa calcola la frazione tra parentesi. Il risultato:

F V = 5000 (1 + 0, 00288) 2 * 12

$FV=5000(1+0,00288)^{{2*12}}$

Somma i numeri tra parentesi. Il risultato:

F V = 5000 (1, 00288) 2 * 12

$FV=5000(1.00288)^{{2*12}}$

Risolvi la moltiplicazione all`interno dell`esponente (l`ultima parte sopra la parentesi chiusa). Il risultato dovrebbe assomigliare a questo:

F V = 5000 (1, 00288) 24

$FV=5000(1.00288)^{{24}}$

Alza il numero tra parentesi alla potenza dell`esponente. Questo può essere fatto su una calcolatrice inserendo prima il valore tra parentesi (1.00288 nell`esempio), premendo il pulsante

X y

$x^{y}$ , e quindi inserendo l`esponente (24 in questo caso), dopodiché si preme Invio. Il risultato di questo esempio è

F V = 5000 (1, 0715)

$FV=5000(1.0715)$ .

Infine, moltiplica il principale per il numero tra parentesi. Il risultato nell`esempio è di € 5.000 x 1.0715 = 5 €.357,50. Questo è il saldo del conto alla fine del secondo anno.

Immagine titolata Calculate Compound Interest Step 9

5. Sottrarre il principale dalla tua risposta. Questo restituisce l`importo degli interessi.

Sottrarre il capitale di € 5.000 dal valore futuro di 5€.357,50 e ricevi 5€.375,50 - 5€.000 = 357,50 €

Hai guadagnato € 357,50 di interessi dopo due anni.

Parte 3 di 3: Calcolo dell`interesse composto con pagamenti regolari

Immagine titolata Calculate Compound Interest Step 10

1. Impara la formula. I calcoli dell`interesse composto possono crescere ancora più velocemente se si effettuano depositi regolari, come il trasferimento di un importo mensile su un conto di risparmio. La formula è più lunga di quella utilizzata per calcolare l`interesse composto senza pagamenti regolari, ma segue gli stessi principi. La formula è la seguente:

F V = P (1 + \frac{io}{C})^{n * C} + R ((1 + \frac{io}{C})^{n * C} - 1) \frac{io}{C}

$FV=P(1+{frac{i}{c}})^{{n*c}}+{frac{R((1+{frac{i}{c}})^{{n *c}}-1)}{{frac{i}{c}}}}$ Anche le variabili nell`equazione sono le stesse dell`equazione precedente, con un`aggiunta:

`P` è il principale.
`i` è il tasso di interesse annuo.
`c` è la frequenza del tasso di interesse e rappresenta il numero di volte in cui l`interesse viene composto annualmente.
`n` è il numero di anni.
`R` è l`importo del contributo mensile.

Immagine titolata Calculate Compound Interest Step 11

2. Compila le variabili. Per calcolare il valore futuro di questo tipo di conto, è necessario il capitale (o valore attuale) del conto, il tasso di interesse annuo, la frequenza degli interessi, il numero di anni calcolati e l`importo del contributo mensile. Queste informazioni dovrebbero essere nel tuo contratto di investimento.

Assicurati di convertire il tasso di interesse annuale in un numero decimale. Puoi farlo dividendo la percentuale per 100. Ad esempio, supponendo il tasso di interesse sopra del 3,45%, dividiamo 3,45 per 100 e ottieni 0,0345.

Per la frequenza degli interessi, si utilizza il numero di volte all`anno in cui viene calcolato l`interesse. Ciò significa numero annuale 1, mensile 12 e giornaliero 365 (non preoccuparti degli anni bisestili).

Immagine titolata Calculate Compound Interest Step 12

3. Compila le variabili. Continuiamo con l`esempio sopra: supponiamo che tu decida di trasferire € 100 al mese sul tuo conto. A proposito di questo conto, con un capitale di € 5.000, l`interesse composto è calcolato mensilmente con un tasso di interesse annuo del 3,45%. Calcoleremo la crescita del conto in due anni.

La formula finale che utilizza queste informazioni è la seguente:

F V = 5000 (1 + 0, 0345 12)^{2 * 12} + 100 ((1 + 0, 0345 12)^{2 * 12} - 1) \frac{0, 0345}{12}

$FV=5000(1+{frac{0.0345}{12}})^{{2*12}}+{frac{100((1+{frac{0.0345}{12}}) ^{{2 *12}}-1)}{{frac{0.0345}{12}}}}$

Immagine titolata Calculate Compound Interest Step 13

4. Risolvi l`equazione. Ancora una volta, non dimenticare l`ordine corretto delle operazioni. Ciò significa che inizi calcolando i valori tra parentesi.

Per prima cosa risolvi le frazioni tra parentesi. Ciò significa dividere `i` per `c` in tre punti, tutti per lo stesso risultato di 0,00288. Ora l`equazione si presenta così:

F V = 5000 (1 + 0, 00288) 2 * 12 + 100 ((1 + 0, 00288) 2 * 12 - 1) 0, 00288

$FV=5000(1+0.00288)^{{2*12}}+{frac{100((1+0.00288)^{{2*12}}-1)}{0.00288}}$

Risolvi l`addizione tra parentesi. Ciò significa che aggiungi 1 al risultato della parte precedente. Così:

F V = 5000 (1, 00288) 2 * 12 + 100 ((1, 00288) 2 * 12 - 1) 0, 00288

$FV=5000(1.00288)^{{2*12}}+{frac{100((1.00288)^{{2*12}}-1)}{0.00288}}$

Risolvi la moltiplicazione all`interno degli esponenti. Ciò significa moltiplicare i due numeri che sono più piccoli e al di sopra delle parentesi di chiusura. Nell`esempio: 2 x 12 = 24. Così:

F V = 5000 (1, 00288) 24 + 100 ((1, 00288) 24 - 1) 0, 00288

$FV=5000(1.00288)^{{24}}+{frac{100((1.00288)^{{24}}-1)}{0.00288}}$

Risolvi gli esponenti. Ciò significa aumentare l`importo tra parentesi con il risultato dell`ultimo passaggio. Su una calcolatrice questo viene fatto inserendo il valore tra parentesi (1,00288 nell`esempio), premere

X y

$x^{y}$ e inserisci il valore dell`esponente (24). Così:

F V = 5000 (1, 0715) + 100 (1, 0715 - 1) 0, 00288

$FV=5000(1.0715)+{frac{100(1,0715-1)}{0.00288}}$

sottrarre. Sottrarre 1 dal risultato dell`ultimo passaggio nella parte destra dell`equazione (1,0715 - 1). Così:

F V = 5000 (1, 0715) + 100 (0, 0715) 0, 00288

$FV=5000(1.0715)+{frac{100(0.0715)}{0.00288}}$

Moltiplicare. Ciò significa moltiplicare il capitale per il valore all`interno della prima serie di parentesi e il contributo mensile per lo stesso valore tra parentesi. Così:

F V = 5357, 50 + 7, 15 0, 00288

$FV=5357,50+{frac{7,15}{0,00288}}$

Dividi la frazione. Così:

F V = 5357, 50 + 2482, 64

$FV=5357.50+2482.64$

Addizionare. Infine, somma i due numeri per ottenere il valore futuro del conto. Quindi: 5€.357,50 + 2€.482,64 = 7€.840.14. Questo è il valore del conto dopo i due anni.

Immagine titolata Calculate Compound Interest Step 14

5. Sottrarre il capitale e pagamenti. Per calcolare gli interessi maturati, devi sottrarre l`importo che hai depositato. Ciò significa sommare il capitale, 5€.000, al valore totale delle somme depositate, quindi: 24 contributi (2 anni x 12 mesi/anno) volte i 100€ che hai versato ogni mese, per un totale di 2400€. Il totale è di 5€.000 + 2€.400 = 7400€. Estrarre 7€.400 di sconto sul valore futuro di 7€.840,14, e hai l`importo degli interessi, € 440,14.

Immagine titolata Calculate Compound Interest Step 15

6. Espandi il tuo calcolo. Per vedere davvero il vantaggio dell`interesse composto, immagina di continuare a depositare denaro sullo stesso conto ogni mese per 20 anni (anziché due). In questo caso, il valore futuro diventa circa 45.000 dollari, anche se spendi solo 29 €.000, il che significa che il tuo interesse maturato è di € 16.000 ammonta a.

Consigli

Puoi anche calcolare facilmente l`interesse composto utilizzando un calcolatore di interessi online. Puoi trovare un esempio sul sito web del governo degli Stati Uniti: https://www.investitore.gov/tools/calculators/compound-interest-calculator.
Un modo rapido per determinare l`interesse composto è la "regola del 72". Inizia dividendo 72 per l`importo degli interessi che ottieni, diciamo 4%. Quindi in questo caso 72/4 = 18. Questo risultato, 18, è approssimativamente il numero di anni necessari per raddoppiare il tuo investimento al tasso di interesse attuale. Tieni presente che la regola 72 è solo una rapida approssimazione, non un risultato esatto.
Puoi anche utilizzare questi calcoli per eseguire calcoli "what if" che possono dirti quanto guadagnerai a seconda del tasso di interesse, del capitale, del tasso di interesse o del numero di anni.