Calcolo degli Interessi

Contenuto

Passi

La maggior parte delle persone conosce il concetto di interesse, ma non tutti sanno come calcolarlo. L`interesse è il valore aggiunto a un prestito o un anticipo per pagare l`uso del denaro di altre persone in un periodo di tempo. Gli interessi possono essere calcolati in tre modi. L`interesse ordinario è il più facile da calcolare e generalmente si applica ai prestiti a breve termine. L`interesse composto è un po` più complicato e vale di più. Dopotutto, la composizione costante degli interessi crescerà più velocemente e questa è la formula utilizzata dalla maggior parte delle banche per i prestiti ipotecari. Le informazioni necessarie per tutti questi calcoli sono generalmente le stesse, ma la matematica è leggermente diversa per ciascuno.

Passi

Metodo 1 di 3: calcolo dell`interesse semplice

Immagine titolata Calculate Interest Step 1

1. Determina l`importo principale. Il capitale è la quantità di denaro che utilizzerai per calcolare gli interessi. Questo può essere un importo che depositi su un conto di risparmio o che metti in una sorta di investimento. In tal caso puoi calcolare gli interessi che guadagni. L`alternativa è che se prendi in prestito denaro, ad esempio per un mutuo, il capitale è l`importo che prendi in prestito e puoi calcolare gli interessi dovuti.

In entrambi i casi, sia che tu stia per riscuotere o pagare interessi, l`importo del capitale è generalmente simboleggiato dalla variabile P.
Ad esempio, se hai preso in prestito $ 2.000 da un amico, quel $ 2.000 è il capitale.

Immagine titolata Calculate Interest Step 2

2. Determina l`interesse. Prima di poter calcolare di quanto capitale aumenterà di valore, è necessario conoscere il tasso di interesse a cui aumenterà il capitale. Questo è il tuo interesse. L`interesse è generalmente pubblicizzato o concordato tra le parti prima della concessione del prestito.

Ad esempio, supponiamo che tu abbia prestato denaro a un amico con l`accordo che dopo sei mesi restituirà i $ 2000 con un interesse dell`1,5%. L`interesse una tantum è dell`1,5%. Ma prima di poter utilizzare la percentuale dell`1,5%, devi convertirla in un decimale. Per convertire la percentuale in decimale, dividi la percentuale per 100:

1,5% 100=0,015.

Immagine titolata Calculate Interest Step 3

3. Controlla la durata del prestito. Il termine è un altro nome per la durata del prestito. In alcuni casi, accetti la durata del prestito prendendo in prestito l`importo. Ad esempio: la maggior parte dei mutui ha una durata fissa. In molti casi, con un prestito privato, mutuatario e prestatore concorderanno un termine prestabilito.

È importante che la durata del termine corrisponda al tasso di interesse, o almeno sia misurata nelle stesse unità. Ad esempio: se si tratta di un tasso di interesse annuo, allora anche la durata deve essere misurata in anni. Se il tasso è pubblicizzato come 3% annuo, ma il prestito è solo per sei mesi, allora stai calcolando un tasso di interesse annuo del 3% su un periodo di 0,5 anni.

Un altro esempio: se il tasso concordato è dell`1% al mese e prendi in prestito il denaro per sei mesi, il termine per il calcolo è di sei mesi.

Immagine titolata Calculate Interest Step 4

4. Calcola l`interesse. Per calcolare l`interesse, moltiplicare il capitale per il tasso di interesse e la durata del prestito. Questa formula può essere espressa algebricamente come:

io = P * R * T

$I=P*r*t$

Utilizzando l`esempio di prestito a un amico sopra, il preside (

P

$P$ ) pari a $ 2000 e la percentuale (

R

$R$ ) è 0,015 su un periodo di sei mesi. Poiché l`accordo in questo esempio era per una durata di sei mesi, la variabile

T

$T$ in questo caso 1. Quindi calcola l`interesse come segue:

io = P R T = (2000) (0, 015) (1) = 30

$I=Stampa=(2000)(0,015)(1)=30$ . Quindi gli interessi dovuti sono di € 30.

Se vuoi calcolare l`intero importo dovuto (A) con gli interessi e i proventi del capitale, utilizza la formula

un = P (1 + R T)

$A=P(1+rt)$ . Questo calcolo si presenta così:

un = P (1 + R T)

$A=P(1+rt)$

un = 2000 (1 + 0, 015 * 1)

$A=2000(1+0,015*1)$

un = 2000 (1, 015)

$A=2000(1.015)$

un = 2, 030

$A=2.030$

Immagine titolata Calculate Interest Step 5

5. Prova un altro esempio. Supponi di depositare $ 5.000 in un conto di risparmio con un interesse annuo del 3%. Dopo soli tre mesi ritiri il denaro, insieme agli eventuali interessi.

un = P (1 + R T)

$A=P(1+rt)$

un = 5000 (1 + 0, 03 * 0, 25)

$A=5000(1+0,03*0,25)$

un = 5000 (1, 0075)

$A=5000(1.0075)$

un = 5037, 5

$A=5037,5$

In tre mesi guadagneresti 37,50€ di interessi.

Si noti che t=0,25, perché tre mesi è un quarto (0,25) del periodo originale di un anno.

Metodo 2 di 3: Calcola l`interesse composto

Immagine titolata Calculate Interest Step 6

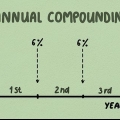
1. Capire cos`è l`interesse composto. L`interesse composto significa che quando guadagni interessi, l`interesse viene aggiunto all`importo nel tuo account e inizi a guadagnare (o pagare) interessi in aggiunta agli interessi. Un semplice esempio: se depositi $ 100 al 5% di interesse all`anno, alla fine dell`anno avrai guadagnato $ 5 di interesse. Se lo rimetti nel tuo account, entro la fine del secondo anno avrai guadagnato il 5% di $ 105, non solo i $ 100 originali. Nel tempo, questo può aumentare in modo molto significativo.

La formula per calcolare il valore (A) dell`interesse composto è la seguente:

$un = P (1 + \frac{R}{n})^{n T}$ $A=P(1+{frac{r}{n}})^{{nt}}$

Immagine titolata Calculate Interest Step 7

2. Sapere cosa significa il principale. Come per gli interessi semplici, il calcolo inizia con l`importo del capitale. Il calcolo è lo stesso sia che tu stia calcolando gli interessi sul denaro preso in prestito o prestato. Il principale è generalmente indicato dalla variabile

P

$P$ .

Immagine titolata Calculate Interest Step 8

3. Determina la percentuale. Il tasso di interesse deve essere concordato prima del prestito e visualizzato come numero decimale per il calcolo. Sappi che la percentuale può essere convertita in decimale dividendola per 100 (o più velocemente, spostando le due posizioni decimali a sinistra). Assicurati di sapere per quale periodo si applica il tasso di interesse. La percentuale ha

R

$R$ come simbolo.

Ad esempio, una società di carte di credito può presentare il proprio interesse come 15% annuo. Tuttavia, gli interessi sono generalmente calcolati su base mensile, quindi probabilmente vorrai sapere qual è il tasso di interesse mensile. In tal caso, lo dividi per 12 e ottieni un interesse mensile dell`1,25%. Queste due percentuali, 15% all`anno e 1,25% al mese, sono uguali tra loro.

Immagine titolata Calculate Interest Step 9

4. Sapere quando l`interesse è composto. L`interesse composto significa che l`interesse viene calcolato periodicamente e aggiunto all`importo principale. Per alcuni prestiti questo può accadere una volta all`anno. Per altri, è ogni mese o ogni trimestre. Devi sapere con quale frequenza gli interessi saranno composti all`anno.

Se l`interesse è composto annualmente, allora n=1.

Se l`interesse è composto trimestralmente, allora denaro n=4.

Immagine titolata Calculate Interest Step 10

5. Conosci la durata del prestito. Il termine è il periodo durante il quale verranno calcolati gli interessi. La durata è generalmente indicata in anni. Se devi calcolare l`interesse su un periodo diverso, devi convertirlo in anni.

Ad esempio: con un prestito di un anno,

T = 1

$t=1$ . Tuttavia, con un termine di 18 mesi,

T = 1, 5

$t=1,5$ .

Immagine titolata Calculate Interest Step 11

6. Determina le variabili della situazione. In questo esempio, supponiamo di depositare $ 5.000 in un conto di risparmio con il 5% di interessi mensili composti. Qual è il valore di quel conto dopo tre anni?

Per prima cosa determina quali variabili sono necessarie per risolvere il problema. In questo caso:

P = 5000

$P=5000$

R = 0, 05

$r=0,05$

n = 12

$n=12$

T = 3

$t=3$

Immagine titolata Calculate Interest Step 12

7. Applicare la formula e calcolare l`interesse composto. Una volta capito cosa bisogna fare e quali variabili sono necessarie, applicale alla formula per calcolare il tasso di interesse.

Nel problema precedente si presenta così:

un = P (1 + \frac{R}{n})^{n T}

$A=P(1+{frac{r}{n}})^{{nt}}$

un = 5000 (1 + 0, 05 12)^{12 * 3}

$A=5000(1+{frac{0,05}{12}})^{{12*3}}$

un = 5000 (1 + 0, 00417) 36

$A=5000(1+0,00417)^{{36}}$

un = 5000 (1, 00417) 36

$A=5000(1.00417)^{{36}}$

un = 5000 (1, 1616)

$A=5000(1,1616)$

un = 5808

$A=5808$

Quindi dopo tre anni di interessi composti hai un importo di € 808, oltre ai € 5000 originariamente depositati.

Metodo 3 di 3: Calcola l`interesse composto ricorrente

Immagine titolata Calculate Interest Step 13

1. Capire cos`è l`interesse composto revolving. Come hai visto nell`esempio precedente, l`interesse composto cresce più velocemente dell`interesse semplice aggiungendo l`interesse al capitale in determinati momenti. La compilazione trimestrale è più preziosa di quella annuale. La compilazione mensile è ancora più preziosa di quella annuale. La situazione più redditizia sarebbe quando l`interesse è composto costantemente, cioè in ogni momento. Non appena l`interesse può essere calcolato, viene aggiunto al conto e aggiunto al capitale. Questo è ovviamente solo un caso teorico.

Utilizzando un po` di matematica, i matematici hanno sviluppato una formula per simulare l`interesse che viene continuamente composto e aggiunto al conto. Questa formula, utilizzata per calcolare l`interesse composto revolving, è:

$un = P e R T$ $A=Pe^{{rt}}$

Immagine titolata Calculate Interest Step 14

2. Conoscere le variabili per il calcolo dell`interesse. La formula dell`interesse composto revolving è molto simile alle situazioni precedenti, ma con alcune piccole modifiche. Le variabili per la formula sono:

un

$un$ è il valore futuro (o importo) di denaro che varrà il prestito dopo aver composto gli interessi.

P

$P$ è il principale.

La costante

e

$e$ . Sebbene sembri una variabile, in realtà è una costante. La lettera

e

$e$ è un numero speciale chiamato "costante di Eulero", dal nome del matematico Leonard Euler che ne scoprì le proprietà.

La maggior parte delle calcolatrici grafiche avanzate dispone di un pulsante per

e X

$e^{x}$ . Se si preme questo pulsante, con il numero 1, quindi

e 1

$e^{1}$ , poi vedi che il valore di

e

$e$ è di circa 2.718.

R

$R$ è l`interesse per anno.

T

$T$ è la durata del prestito, in anni.

Immagine titolata Calculate Interest Step 15

3. Conosci i dettagli del tuo prestito. Le banche di solito utilizzano l`interesse composto revolving per i mutui. Supponiamo di avere 200€.000 vogliono prendere in prestito con un interesse del 4,2% per un mutuo di 30 anni. Quindi le variabili che utilizzerai per questo calcolo sono:

P = 200.000

$P=200.000$

e

$e$ , di nuovo, non una variabile ma la costante 2.718.

R = 0, 042

$r=0,042$

T = 30

$t=30$

Immagine titolata Calculate Interest Step 16

4. Utilizzare la formula per calcolare l`interesse. Applica i valori alla formula per calcolare l`importo degli interessi che dovrai pagare sul prestito a 30 anni.