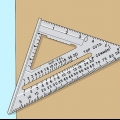
Usare la Regola 3 4 5 per Determinare gli Angoli Retti: 4 Passaggi (con Immagini)

Contenuto

Passi
- Metodo 1 di 1: Usare la regola 3-4-5
Consigli
Necessità

Una delle sfide per creare angoli è farli squadrare. Ovviamente la tua stanza non deve avere angoli perfettamente retti, ma è sempre utile avvicinarsi di 90 gradi il più vicino possibile. Altrimenti vedrai che le pareti non sono completamente a filo con moquette o piastrelle. Il metodo 3-4-5 è utile anche per piccoli progetti di lavorazione del legno, per assicurarsi che tutte le parti si adattino esattamente come previsto.

Passi

Metodo 1 di 1: Usare la regola 3-4-5

Immagine titolata Usa la regola 3 4 5 per costruire angoli quadrati Passaggio 1

1. Comprendi il metodo 3-4-5. Se un triangolo ha i lati rispettivamente di 3, 4 e 5 metri (o qualsiasi altra unità), allora abbiamo a che fare con un triangolo rettangolo con un angolo di 90º tra i lati corti. Se riesci a "trovare" questo triangolo nel tuo angolo, allora sai per certo che l`angolo è quadrato. Questo si basa su il teorema di Pitagora , potresti ricordare dalla matematica: A+B=C in un triangolo rettangolo. C è il lato più lungo (ipotenusa) e A e B sono i due lati più corti.

3-4-5 è una misura facile da controllare perché i numeri sono piccoli e perché sono numeri interi. La formula è assolutamente corretta: 3+4=9 + 16=25=5.

Immagine titolata Usa la regola 3 4 5 per costruire angoli quadrati Passaggio 2

2. Misura tre unità dall`angolo lungo un lato. Questo può essere metri o centimetri o altre unità. Metti un segno alla fine di tre unità.

Puoi moltiplicare qualsiasi numero per lo stesso numero e funzionerà comunque. Ad esempio si possono utilizzare anche 30-40-50 centimetri, oppure nel caso di una stanza grande 6-8-10 o 9-12-15 metri.

Immagine titolata Usa la regola 3 4 5 per costruire angoli quadrati Passaggio 3

3. Misura quattro unità dall`angolo lungo l`altro lato. Usando la stessa unità, misura (si spera) con un angolo di 90 lungo l`altro lato. Segna il punto alla fine delle quattro unità.

Immagine titolata Usa la regola 3 4 5 per costruire angoli quadrati Passaggio 4

4. Misurare la distanza tra i segni. Se la distanza è 5 unità hai un angolo retto.

Se la distanza è inferiore a 5 unità, l`angolo è inferiore a 90º. Quindi allontana leggermente i lati.

Se la distanza è maggiore di 5 unità, l`angolo è maggiore di 90º. Quindi sposta i lati l`uno verso l`altro.

Consigli

Questo metodo può fornire risultati più precisi di un quadrato quadrato, perché di solito sono troppo piccoli per effettuare misurazioni precise su scala più ampia.
Più grande è l`unità, più preciso sarà il risultato.